消声室声学性能评价方法探讨
2012-11-15蒲志强姚小兵鄂治群
蒲志强,姚小兵,孙 磊,鄂治群
(中国测试技术研究院,四川 成都 610021)
0 引 言
消声室是电声测试和噪声测试中极其重要的实验场所,其作用是提供一个自由场或半自由场空间的低噪声测试环境。
2006年发布的JJF 1147-2006《消声室和半消声室声学特性校准规范》详细地规定了消声室和半消声室声学特性的测量和评价方法[1],该规范参考采用ISO 3745-2003附录A[2]。消声室主要技术指标有两项:(1)自由声场的频率范围和空间范围;(2)本底噪声。其中,消声室和半消声室的自由场频率范围和空间范围是根据测量位置上的声压级与满足反平方律的声压级之间的偏差来确定的。
但是,完全按照JJF 1147-2006提供的计算方法得出的理论曲线和测量曲线存在“远端对齐”的现象,从而无法有效地对消声室和半消声室的自由声场特性进行评价。本文以国内某半消声室的测试数据为例,对该现象的产生原因进行了分析并提出优化改进办法。
1 测量过程和测量结果分析
依照JJF 1147-2006选取测试路径。测试用声源信号为粉红噪声,声源位置为半消声室地面几何中心。沿着测试路径以10cm为步长远离声源完成所有测点的声压级测量,每个测点测试32 s的等效连续声压级。
依据JJF 1147-2006计算得到反平方律声压级,即满足反平方律的理论值。然后将测量位置上的声压级与理论值进行比较。
1000Hz的测试结果如图1所示。

图1 1000Hz频点测量结果
图1中可以看出,随着测试距离r增加,计算得到的反平方律声压级Lp(r)与测量值偏差的绝对值有逐渐减小的趋势,呈现出不合理的“远端对齐”的现象,即远处测量值与理论值偏差的绝对值更小,自由场特性更好。此现象在依据JJF 1147-2006评价消声室和半消声室的自由场特性中具有普遍性。
表1详细地给出了在1000Hz频率点的声压级测量值与反平方律声压级的偏差。

表1 1000Hz频点声压级偏差
然而理论和公认观点是消声室/半消声室的中间区域应具备较好的自由声场特性,而不是距离中心较远的区域[3-6]。
对于边长为L的立方体消声室,声源放在室中心,在噪声信号的情况下,可以得到与自由声场衰减最大偏差的公式[7]为

式中:Re——能量反射系数;
r——测点到声源的距离;
L——消声室内空间的边长。
由式(1)可以证明,距离声源越近,越接近自由声场理想条件。
但图1及表1清楚表明,在距离声源较近处偏差的绝对值较大,在距离吸声壁面较近处反而偏差的绝对值较小,这与公认的理论和观点不符,使得按照JJF 1147-2006确定自由场半径不可操作。
2 “远端对齐”现象分析
在依据JJF 1147-2006计算反平方律声压级时,引入了参数q,令q=10-0.05Lp,得到关于q和r的线性方程为

以式(2)为数学模型,运用线性最小二乘法可以计算确定a和r0。线性最小二乘法原理是以测量值qi与利用式(2)计算出的q的离差(qi-q)的平方和∑(qi-q)2最小为优化判据,计算出理论曲线的a和r0。
声压级Lp(r)与参数q的函数关系为

因此

图2、图 3、图 4 中给出了 250,1250,5000Hz 3 个测试频点Δq和ΔLp(r)与测试距离之间的关系。
从图中可以看出,随着测试距离的增加,Δq的变化呈现无规律性,而ΔLp(r)均呈现逐渐减小的趋势。

图2 250Hz的数据偏差


图3 1250Hz的数据偏差

图4 5000Hz的数据偏差
3 问题的解决
3.1 参数a和r0的改进求解法
消声室和半消声室自由声场特性的评价是根据不同位置上测量声压级与满足反平方律声压级的偏差。反平方律的声压级大小,取决于参数a和r0。参数a和r0的计算公式为

式中:qi=10-0.05Lpi;
ri——声源假定声中心到测点的距离,m;
N——测点的数目;
Lpi——第i个点的测量声压级,dB。
从式(5)和式(6)中可以看出,参数 a和 r0的值主要取决于测点位置的声压级Lpi的大小。在靠近吸声壁面的区域,因声反射等因素影响使得各测点的声压级不能较好地满足反平方律,如果参加计算,势必影响到计算结果的准确性。而且,可以证明距离声源越远,Lpi测量不确定度对参数a和r0计算结果影响越大。
为此,提出了a和r0的改进求解法,即在计算参数a和r0时,简单舍弃靠近消声室吸声壁面测点的数据。图5和图6直观地显现了此方法的改善效果。

图5 选取10个点拟合效果图
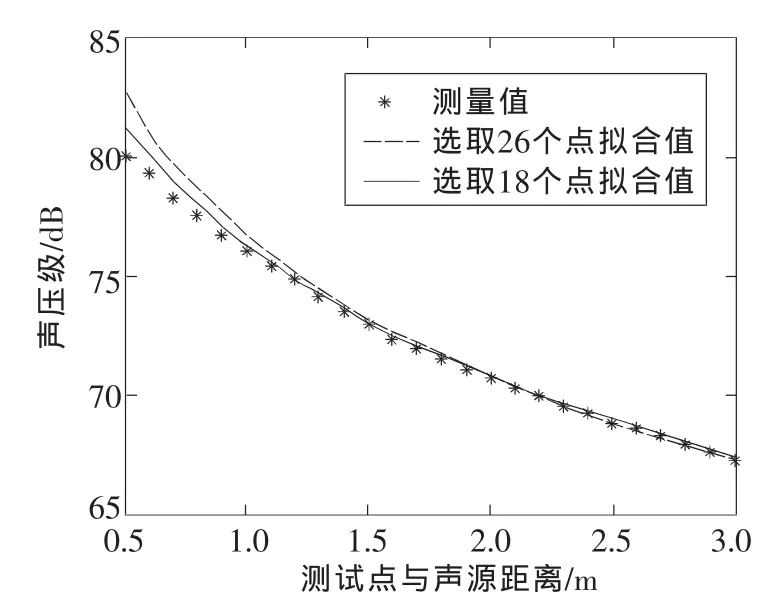
图6 选取18个点拟合效果图
从图5和图6中可以看出,舍弃靠近吸声壁面的测试点的测试数据计算参数a和r0时,能在一定程度上改善不合理的“远端对齐”现象,但存在依据什么原则、数量如何确定等问题。
3.2 非线性最小二乘法
JJF 1147-2006中以式(2)为拟合数学模型,以∑(qi-q)2最小为判据,应用线性最小二乘法来求解a和r0的值,但最终评估量Lp(r)与r却不是线性关系。
在非线性最小二乘法中选用牛顿-高斯算法。采用测试距离1m处的a值和声中心的修正为0作为迭代初值[9]。
图7为规程中的算法和非线性最小二乘法所得拟合的理论曲线比较。
通过图7可以看出,运用非线性最小二乘法得到的拟合曲线比JJF 1147-2006中的线性最小二乘法得到的理论曲线更符合实际情况,适合用来评价消声室和非消声室的自由声场特性,即自由场频率范围和空间范围。

图7 规范中算法和非线性最小二乘法比较
4 结束语
JJF 1147-2006获取自由场频率范围和空间范围的给定方法存在缺陷,“远端对齐”现象导致依据规范评估困难。本文分析出现“远端对齐”现象的原因,并提出2种优经改进方法。
另外,依据测量值计算理论值,再判断测量值与理论的偏差在逻辑上是否存在缺陷也是个值得思考的问题。
[1]JJF 1147—2006消声室和半消声室声学特性校准规范[S].北京:中国计量出版社,2006:6-7.
[2]Acoustics-Determination of sound power level of noise source using sound pressure-precision method for anechoic and hemi anechoic rooms[S].Geneva:ISO 3745-2003:Annex A.
[3]南京大学物理系声学实验室.南京大学消声室[J].物理学报,1975,24(4):252-259.
[4]江泓.消声室的校准与数据处理[J].计量与测试技术,2009,35(6):41-42.
[5]刘克.平板式半消声室测试及仿真计算[J].声学技术,2007,26(5):111-112.
[6]孙广荣.消声室内最大自由声场误差的估算[J].声学技术,1987,6(2):16-18.
[7]孙广荣.消声室自由声场鉴定的几个问题[J].电声技术,2008,32(8):4-5.
[8]朱仁峰.精通Matlab 7[M].北京:清华大学出版社,2006:262-265.
[9]吴玲.全局收敛高斯-牛顿法解非线性最小二乘定位问题[J].火控雷达技术,2003(32):75-80.
