拉格朗日插值多项式对函数的逼近

吴晓红,卢志康

(1. 浙江商业职业技术学院基础部,浙江 杭州 310056;2. 杭州师范大学理学院，浙江 杭州 310036)

吴晓红1,卢志康2

(1. 浙江商业职业技术学院基础部,浙江 杭州 310056;2. 杭州师范大学理学院，浙江 杭州 310036)

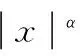
Lagrange插值多项式；逼近度；Chebyshev结点

0 引 言

定理1对任意的α>0,n∈N,n为偶数,n≥n0(α),有

(1)

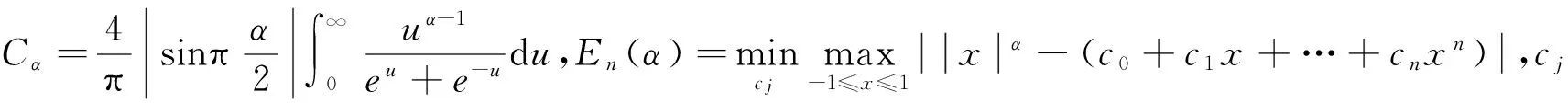
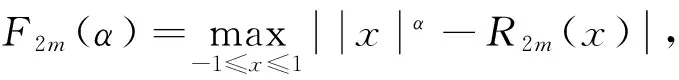
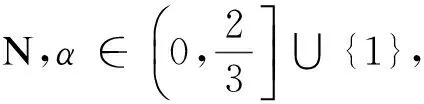
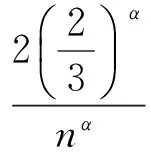
(2)

后来，何国龙等[3]取消了关于α的限制，证明了当α∈(0,1]时，定理都是成立的.

本文给出了达到文献[1]中最佳逼近阶的插值多项式的构造，并得到了更好的逼近系数.

1 主要结果

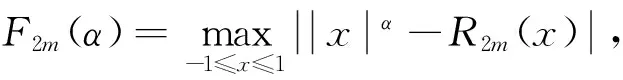
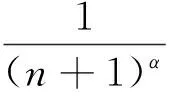
由此得到

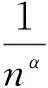
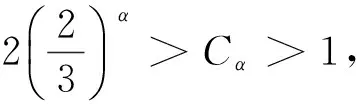
2 引理及其证明

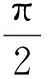
(3)

于是有

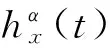
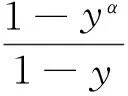
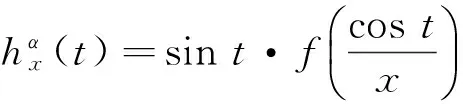
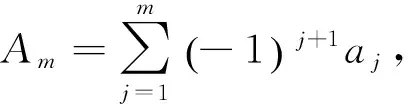
证明当m=2k时，

(-1)m+1Am=(-a1+a2)+(-a3+a4)+…+(-am-3+am-2)+(-am-1+am)≥0

和

(-1)m+1Am=-a1+(a2-a3)+…+(am-2-am-1)+am≤am.

类似地，当m=2k+1时，有

(-1)m+1Am=a1+(-a2+a3)+(-a4+a5)+…+(-am-1+am)≥0

和

(-1)m+1Am=(a1-a2)+(a3-a4)+…(am-2-am-1)+am≤am.

这样，引理2证毕.

引理3当n=2m+1,m∈N，有

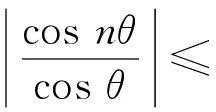
(4)

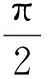
3 定理的证明

这里只给出0≤x≤1的证明，当-1≤x<0时的证明是类似的.

设m∈N,n=2m,0<α≤1，0≤x≤1，记

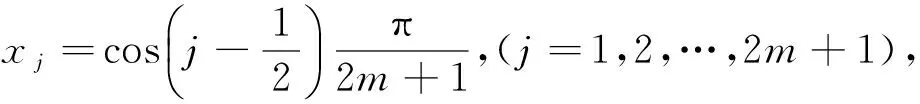
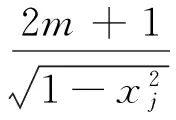
因此

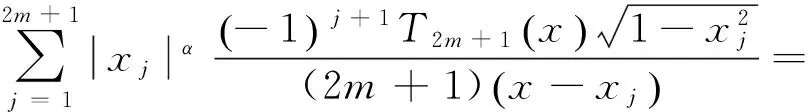
(5)

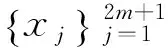
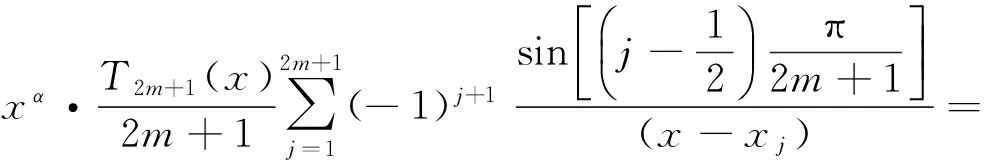
(6)

从而有

xα-R2m(x)=

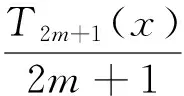
(7)

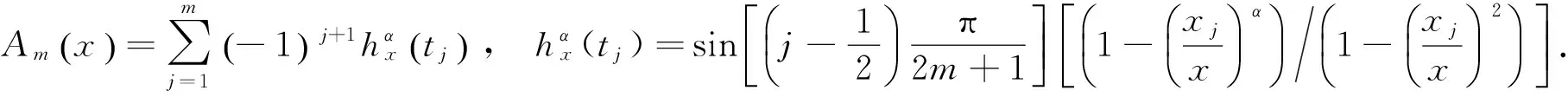
(8)

应用式(8)和引理3得

由此,定理3证毕.

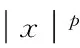
[2] Revers M. On the approximation of certain functions by interpolation polynomials[J]. Bull Austral Math Soc,1998,58(3):505-512.

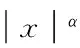
[4] Bernstein S N. Sur la meilleure approximation de|x| par des polynmes de degrés donnés[J]. Acta Math,1913,37 (1):1-57.

[5] Elosse P D. Approximation of powers ofxby polynomials[J]. J Approx Theory,1978,23(1):163-174.

[6] Elosse P D. Chebychev coefficients in approximation of powers ofx[J]. J Approx Theory,1990,63(1):293-302.

[7] Byrne G J, Mills T M, Smith S J. On Lagrange interpolation with equidistant nodes[J]. Bull Austral Math Soc,1990,42(1):81-89.

[8] Revers M. The divergence of Lagrange interpolation for |x|αat equidistant nodes[J]. J Approx Theroy,2000,103(2):269-280.

[9] Varga R S, Carpenter A J. On the Bernstein Conjecture in approximation theory[J]. Const Approx,1985,1(1):333-348.

[10] Brutman L, Passow E. Rational interpolation to |x| at the Chebyshev nodes[J]. Bull Austral Math Soc,1997,56(1):81-86.

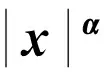
WU Xiao-hong1, LU Zhi-kang2

(1. Department of Basic Courses, Zhejiang Vocational College of Commerce, Hangzhou 310053, China; 2. College of Science, Hangzhou Normal University, Hangzhou 310036, China)

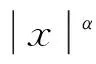
Lagrange interpolation polynomial; approximation; Chebyshev nodes

2012-01-31

浙江省教育厅科研项目(20071352).

吴晓红(1976—)，女，副教授，主要从事函数逼近论研究.E-mail: zjvcc_wxh@126.com

11.3969/j.issn.1674-232X.2012.04.003

O174.41MSC201042A15

A

1674-232X(2012)04-0302-03