不同覆冰长度对110 kV复合绝缘子电位的影响分析

2012-11-14赵冀宁程云霞

河北电力技术 2012年6期

赵冀宁，程云霞

(1.河北省电力公司检修分公司，石家庄 050070;2.浙江台州临海供电局,浙江台州 317000)

我国电力发展进入高速时期，高压线路必将经过覆冰比较严重地区，由于绝缘子覆冰而产生的问题也日益凸显。复合绝缘子具有轻便，维护方便，防污性能好等优点，因此在很多工程中可以取代玻璃和陶瓷绝缘子[1]。例如内蒙古达拉特旗20 kV线路新建工程就采用FPQ-24/6和FXBW-20/70 2种型号的复合绝缘子。但是在绝缘子覆冰严重地区，复合绝缘子的使用还比较少，覆冰情况下的电位分布情况还有待进一步研究[2]。以下以FXBW-110/100型复合绝缘子为例分析不同覆冰长度对绝缘子外部电位的影响。

1 理论分析

目前求解电场的方法很多,主要有数值计算法、解析法、图解法和模拟法[3]。其中后3种方法的应用范围限制较大,数值计算方法近年来得到较广泛的应用和发展[4]。以下采用功能强大、分析电位分布应用广泛的有限元数值计算法来计算户外绝缘子的电位分布。有限元数值计算法以变分原理和剖分插值为基础,用该方法求解电场问题时,首先把电场问题转化为由能量积分求极值的变分问题,然后利用剖分把待求解的场域划分成许多小单元,从而把泛函极值问题简化为普通多元线性代数方程[5]。另外运用有限元数值计算法计算户外绝缘子电位分布还有以下优点：

a. 有限元数值计算法的系数矩阵正定、对称、且稀疏,节省计算机的计算时间[6]。

b. 解决绝缘子覆冰情况下电场分布问题时，涉及到玻璃钢和碳素钢、碳素钢和空气、碳素钢和硫化橡胶、玻璃钢和硫化橡胶、硫化橡胶和空气、硫化橡胶和冰、还有冰和空气7种介质交界面，采用有限元法计算时，交界面边界条件可不作任何处理，且方便建模[7]。

c. 有限元数值计算法建模和剖分比较灵活多变，而绝缘子电场分布模型相对复杂，因此利用有限元数值计算法来处理比较合适。建模过程中充分利用绝缘子的对称结构简化模型。在网格划分过程中，对不同的面采用不同的划分方法。有限远场采用不同精度的自动网格划分，无限远场采用映射网格划分，既提高了计算精度，又减少了网格划分的时间[8]。

2 计算模型

2.1 模型介绍

由于实际中杆塔和导线等因素的影响，绝缘子表面电场和电位分布并不是严格对称的，以下从工程近似角度对模型进行简化，采用轴对称模型在二维平面内简化为1/2面模型。由于是轴对称结构所以选择PLANE121对称单元。解决远场问题采用远场单元INFIN110模拟,也为轴对称的形式[8]；分析类型选择静电场。同时将无穷大的场域分为有限远区域和无限远区域,用远场单元模拟无限远单元区,解决了绝缘子电场模型的开域问题。复合绝缘子计算模型见图1。

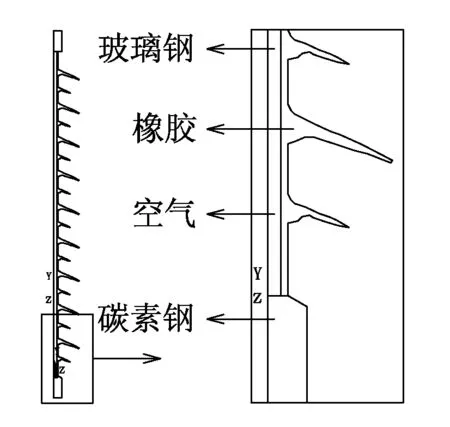
图1 复合绝缘子计算模型

计算中涉及到空气、玻璃钢(复合绝缘子芯棒)、硫化橡胶(伞群护套)、碳素钢(端部金具)和冰等5种媒质，其相对介电常数的选择见表1[9-10]。不同的覆冰长度模型见图2。经过实际考察以及相关文献查询，现假设覆冰都是从第一个大伞群开始沿大伞群向下发展。假设覆冰长度H从0 cm到80 cm每一级间隔为10 cm，见图2。图中的a、b、c、d、e、f、g、h和i对应的覆冰长度分别为0 cm、10 cm、20 cm、30 cm、40 cm、50 cm、60 cm、70 cm和80 cm。

表1 材料参数表

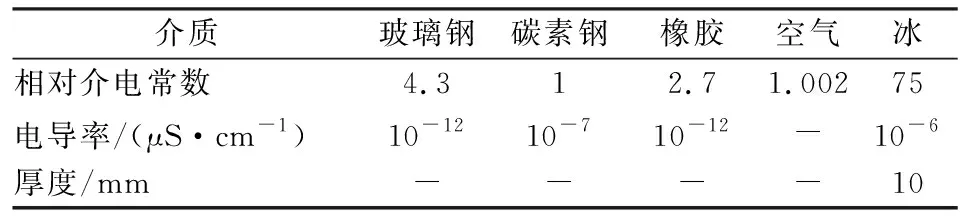
介质玻璃钢碳素钢橡胶空气冰相对介电常数4.312.71.00275电导率/(μS·cm-1)10-1210-710-12-10-6厚度/mm----10

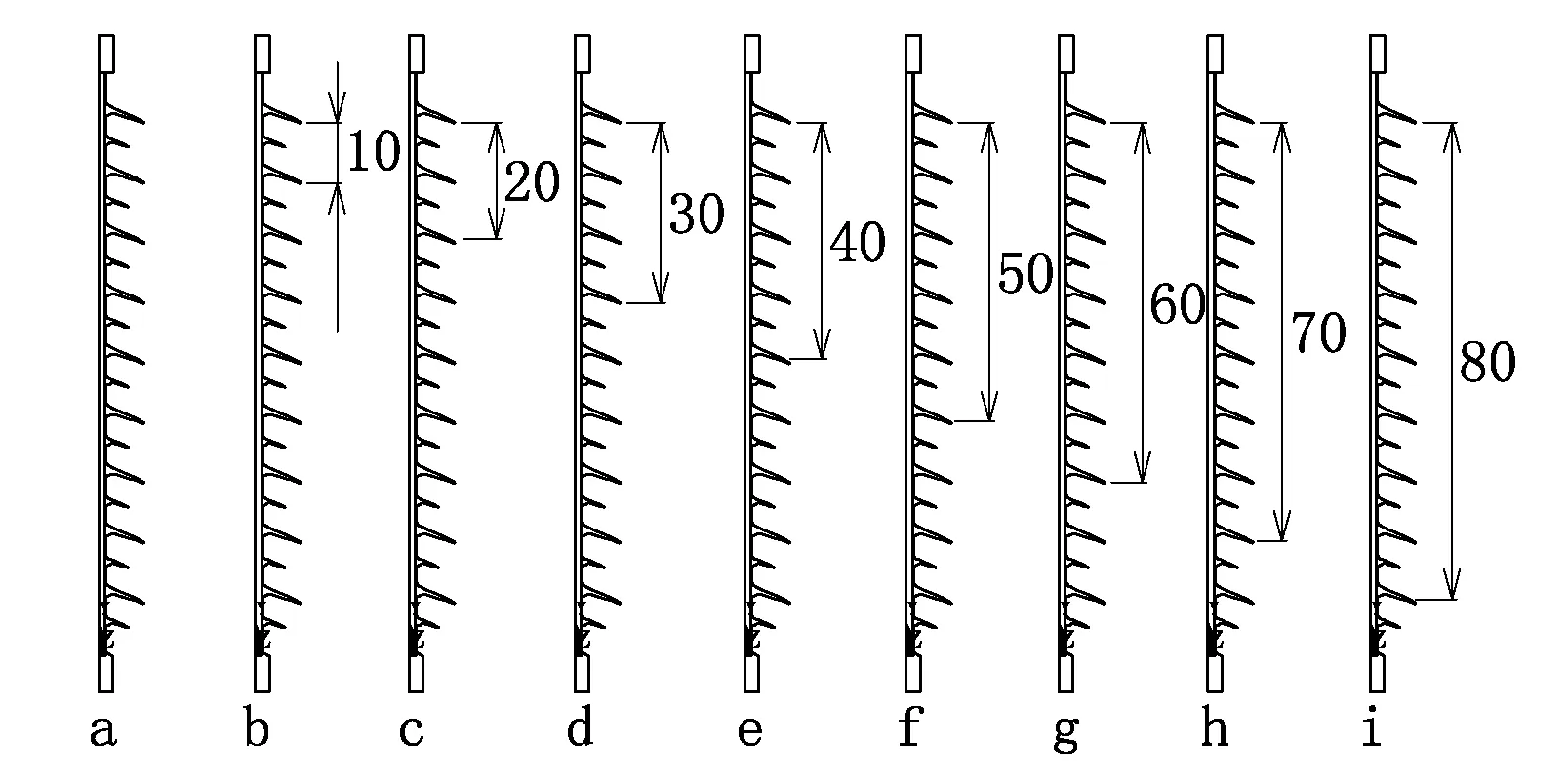
图2 绝缘子覆冰模型(单位：cm)

2.2 模型网格划分

网格划分是否成功与网格划分是否合理、精细密切相关。该模型采用如下方法进行网格划分，以提高计算精度：对有限远场和无限远场采用不同的划分方法，有限远场采用映射网格划分的方法，无限远场采用自由网格划分；自由网格划分过程中选择最高级别的自由网格划分以提高划分的精细度，对有限远场整体进行划分提高计算精度。洁净绝缘子的划分结果见图3。

图3 绝缘子剖分示意

2.3 计算结果

设置下金具边缘电位为110 000 V,设置上金具边缘电位为0 V，点击solve进行计算[7]。得到绝缘子周围的电位分布示意见图4。

图4 绝缘子电位分布示意

3 计算结果分析

利用该模型经过ansys计算不同的覆冰长度绝缘子周围的电位分布示意见图4。由于覆冰绝缘子的放电与绝缘子表面电位的畸变关联较大，因此研究覆冰长度对绝缘子表面电位影响很有意义。选择ansys里的plot菜单下的node获得绝缘子表面各点的电位数据表，将数据导入matlab进行绘图得到绝缘子表面的电位分布如图5所示。

由图5可知，当没有覆冰时，绝缘子表面的电位分布极不均匀；当爬电距离达到200 cm时，电位只下降了11 000 V，也就是说前70%的爬电距离分布着10%的电压，而后30%的爬电距离分布着90%的电压，可见未覆冰绝缘子表面的电位分布是极不均匀的。对比图5中的a到i可知当覆冰的长度小于60 cm时绝缘子表面的电位分布变化较小，等位线的走向和分布也和未覆冰时基本一致；当覆冰长度达到70 cm时，等位线的走向发生了一定的变化，尤其是覆冰的末端等位线畸变严重。覆冰末端前后电位分布比较见图6。