基于EGM的山区爬坡线路绕击跳闸率计算

康 琛，苏红梅，梁贵书，刘晓冬

(1．华北电力大学，河北 保定 071003；2．河北省电力公司电力科学研究院，石家庄 050021)

1 概述

输电线路绕击跳闸率的计算方法主要有规程法[1]、电气几何模型法(EGM)、先导传播模型法、绕击概率模型法等。

电气几何模型法是建立在雷击机理的基础上，以现场数据为基础的工程计算模型，计算方法较为合理、简单，是目前线路绕击分析的主要方法[2-4]。与平原架空输电线路绕击率计算方法不同[5]，输电线路在翻跃山峰时，计算绕击率不仅需要考虑地面倾角因素，还要考虑线路平均高度的变化，以及线路保护角随山坡倾角的变化。通过对山区爬坡线路进行分析研究，对导线平均高度和保护角变化值进行求解，提出山区爬坡线路绕击率计算方法，与传统EGM方法相比，能够提高计算绕击率的合理性。

2 山区爬坡线路绕击率计算方法

2.1 架空线路对地平均高度计算

对于爬坡线路，由于杆塔与坡面不垂直，线路平均高度为导线与地面的平均距离。根据导线与坡面的位置关系，建立导线对地平均高度计算模型，如图1所示。

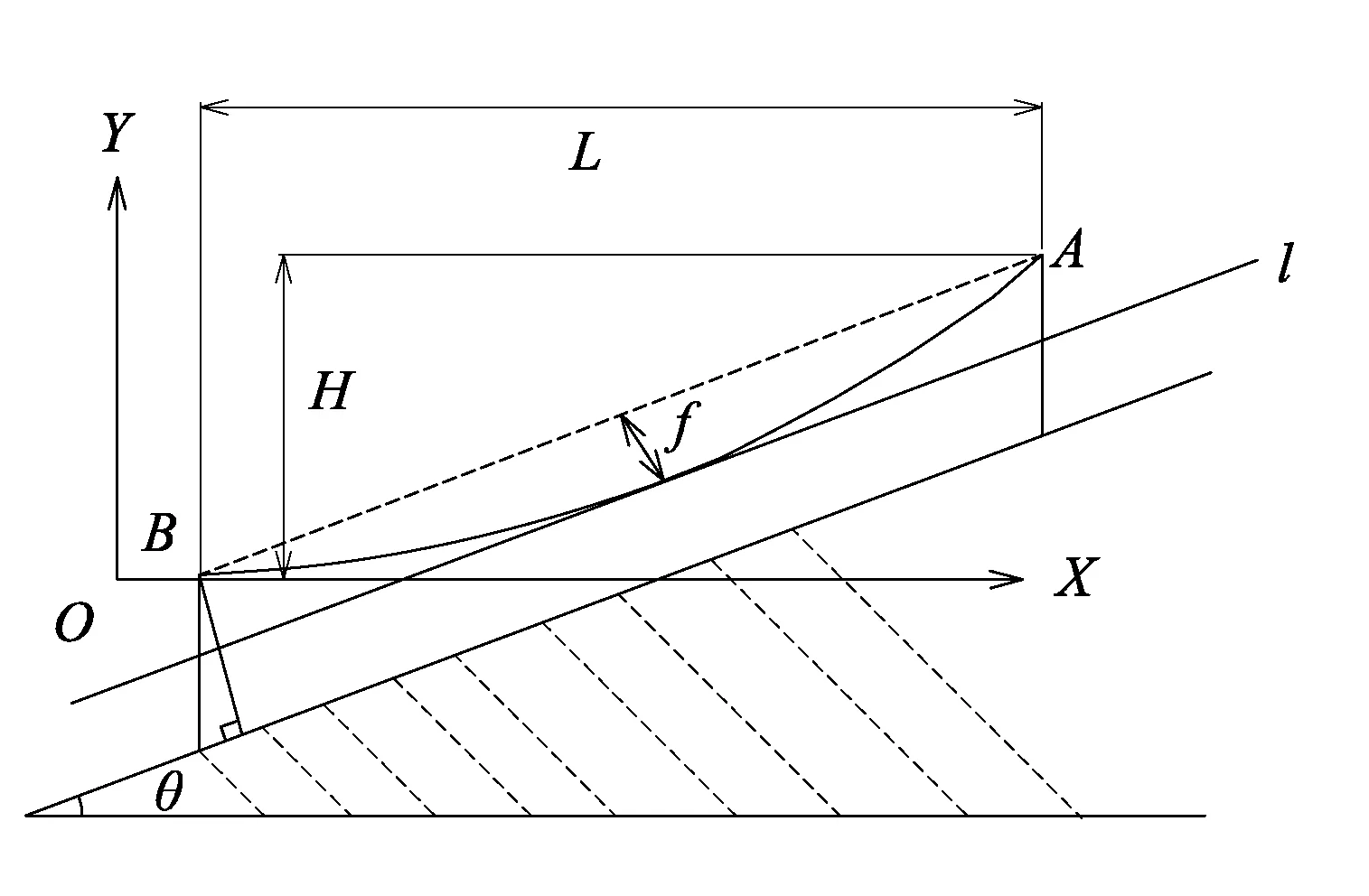
A，B-导线悬挂点；L-档距；H-导线悬挂点高度差； θ-山坡倾角；l-与坡面平行且与导线AB相切的直线

不等高悬点架空线AB的高度满足斜抛物线方程[6]：

(1)

式中：g为导线的自重比载，kg/(m·mm2)；δ为水平应力(即导线最低点应力)，kg/mm2；β为相邻杆塔高差角，与θ大小相同。

斜抛物线方程是以导线最低点O为直角坐标系原点，原点O点可能位于B点左侧或右侧。

设切线l的一般方程：

Ax+By+C=0

(2)

通过与式(1)联立求解，

由架空线平均高度的定义[6]，即架空线上各点相对弧垂最低点的高度差对档距的平均值ha可知：

(3)

(4)

xb=xa-L

(5)

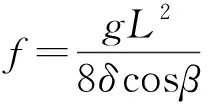
(6)

架空线平均高度

h=ha+Hd·cosθ-f

(7)

式中：Hd为导线悬挂点高度，m；H为相邻杆塔高度差，m。

2.2 保护角计算值

爬坡线路平均高度的变化，使得保护角计算值相对设计值也发生变化，如图2所示。

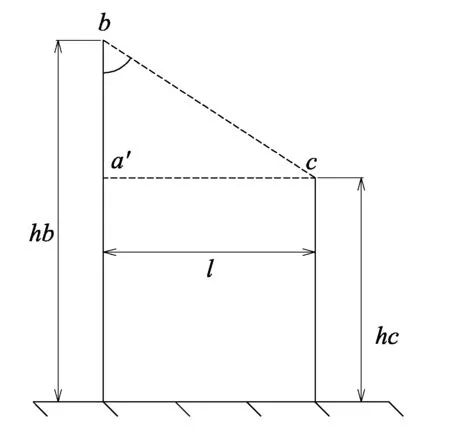
hb、hc-避雷线和导线对地平均高度，m；l-避雷线与导线在坡面上投影之间距离

保护角计算值：

(8)

式中：Hb、Hc为避雷线和导线悬挂点对地高度，m；α为线路保护角设计值。

3 实例分析

以某山区220 kV同塔双回线路某一档距为例，对Ⅱ线各相绕击情况计算分析。

杆塔之间档距555 m，杆塔型号GUZ21，呼高33 m，为同塔双回相线垂直排列，Ⅰ线相序自上而下VWU；Ⅱ线相序自上而下VUW；Ⅰ线上避雷线对V相保护角为26.6°，对W相保护角为19.3。对U相保护角为8.9°。

最小绕击电流Imin=12 kA。

击距系数k值与导线平均高度h有关，采用IEEE工作组推荐的关系式[7]：

当h≤40 m时，k=0.36+0.17ln(43-h) ；

当h>40 m时，k=0.55 。

最大击距通用公式：

F=k2-sin2(α-θg)

跳闸率

雷电定位系统统计得到线路走廊区域实际雷电流幅值概率密度函数f(I)[8-9]：

式中：α=36.4；β=3.1；地闪密度Ng=1.84次/km2·a。

爬坡线路的平均高度计算如表1、图3所示。

表1 不同山坡倾角下的线路平均高度

山坡倾角避雷线平均高度/mV相平均高度/mW相平均高度/mU相平均高度/m5°10°15°20°25°30°35°40°41.85941.14239.94638.27136.11433.46930.32726.66535.25734.52533.30331.58629.36726.63123.35819.51029.28028.61627.50825.94823.92921.43518.44314.91423.30322.70821.71220.31018.49116.23913.52810.318

图3 导线平均高度与山坡倾角关系

从计算结果得知，线路平均高度随山坡倾角增大而迅速减小，V相平均高度的下降趋势比W、U相明显，即避雷线与V相平均高度的差值随着山坡倾角的增大而增大，避雷线与W、U相平均高度的差值随着山坡倾角增大而减小，从而得推导出V相的保护角计算值随着山坡倾角增大而减小，W、U相保护角计算值变化趋势与V相相反，如图4所示。

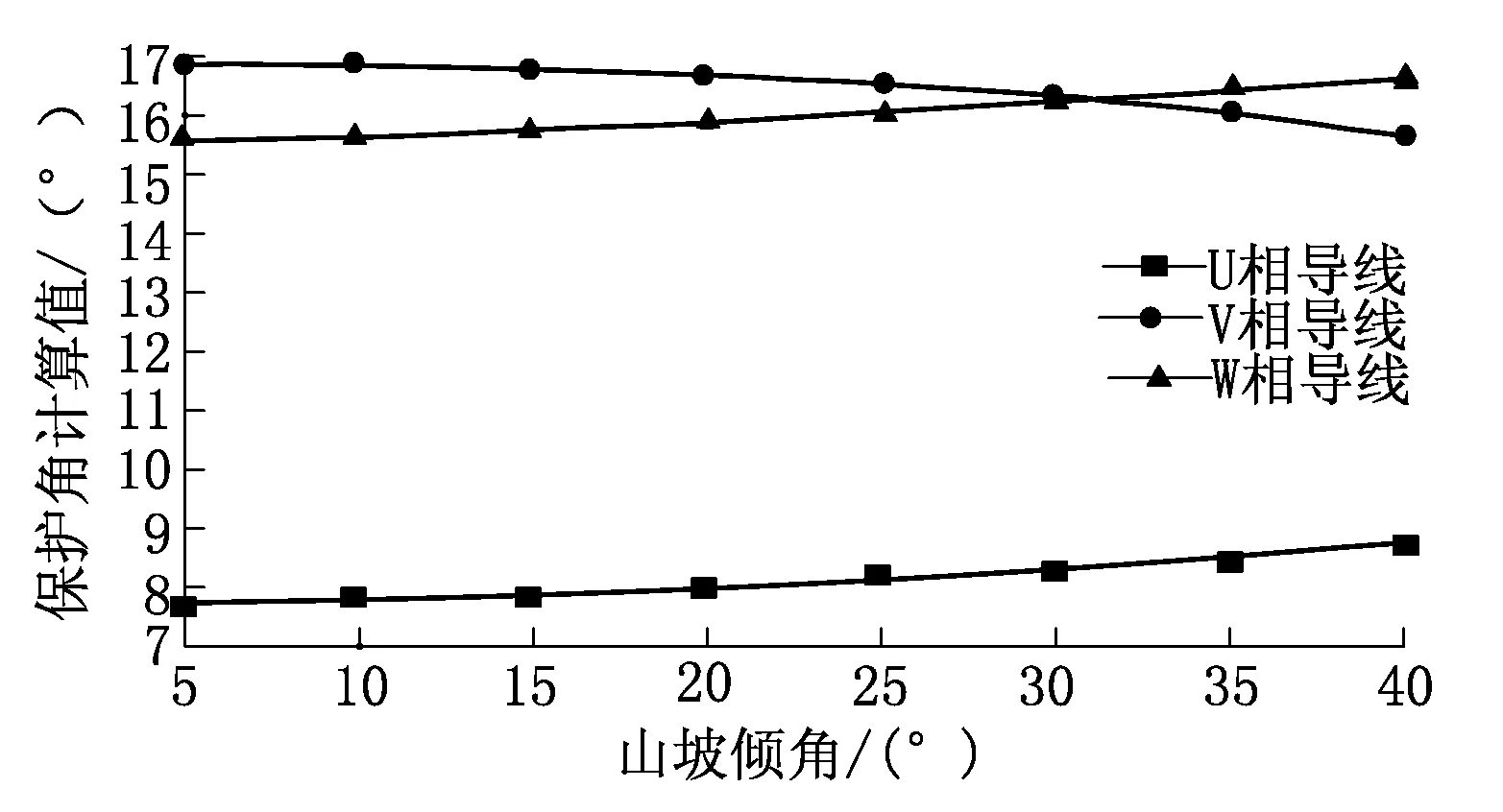
图4 保护角计算值与山坡倾角关系

随着山坡倾角的增大，V相保护角计算值由16.878°降至15.64°，W相保护角计算值由15.557°增至16.594°，U相保护角计算值由7.689 8°增至8.713 7°。

绕击率P与山坡倾角θ关系如图5所示：

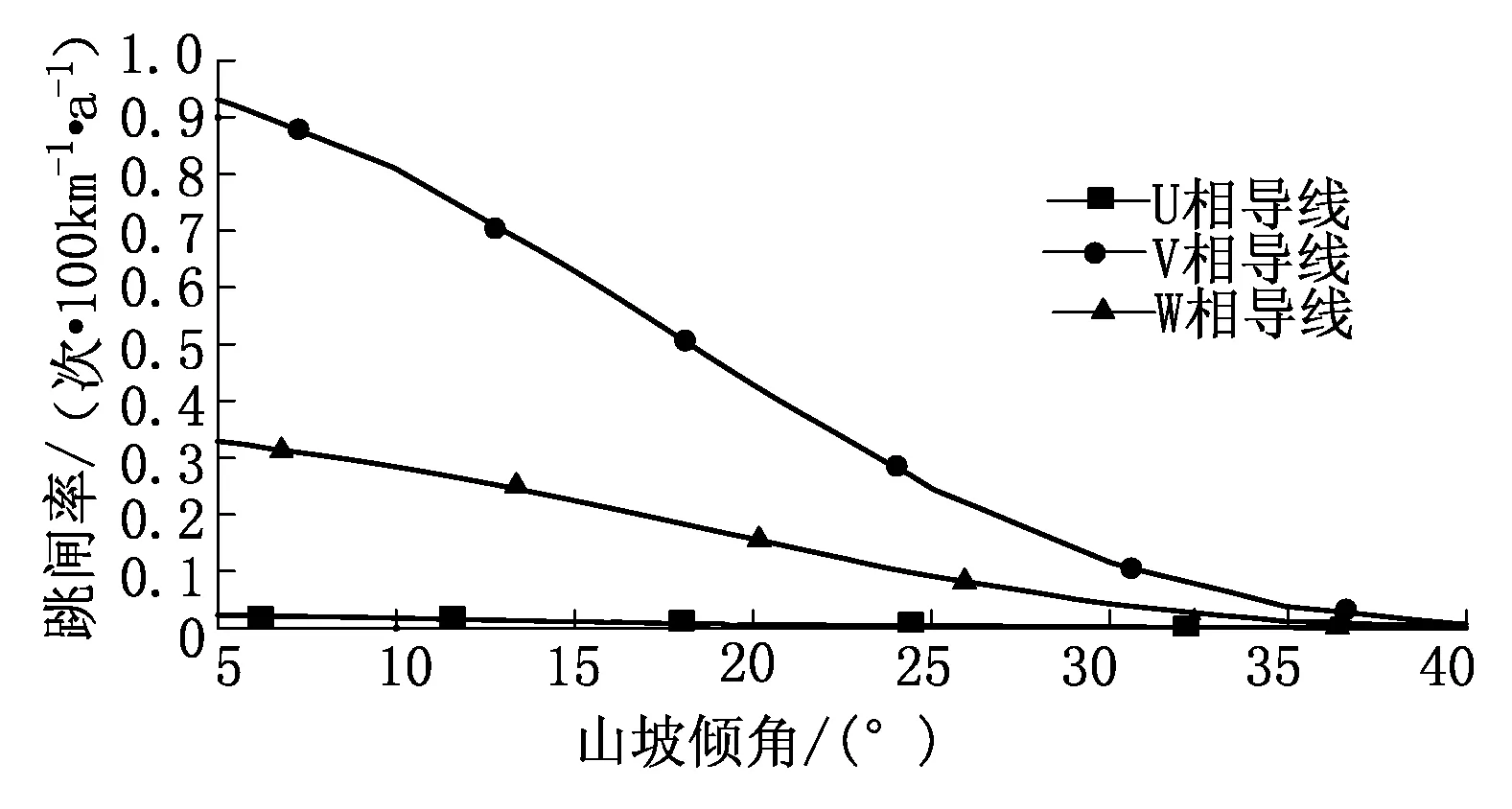
图5 绕击率P与山坡倾角θ关系

由图5得出，V相绕击率远大于W、U相，且V相绕击率下降速度明显快于W、U相，这是由V相平均高度与保护角计算值随着山坡倾角的增大同时减小造成，可推出，在其他相同条件下，山区爬坡线路比平原线路的绕击率低，不易遭遇绕击。在山坡倾角达到35°及以上时，V、W、U相绕击率处于较低水平。

图6为V相与W相在相同雷电流幅值下暴露距离的大小对比，通过比较得出，对于较小雷电流幅值情况下，W相的暴露距离大于V相，在雷电流幅值为16.9 kA下，V、W相暴露距离见表2。

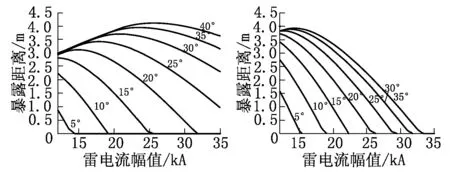
(a) V相 (b) W相图6 暴露距离与雷电流幅值关系

V、W相暴露距离均随山坡倾角的增大而减小，但在山坡倾角小于20°时，W相暴露距离大于V相；

大于20°时，W相暴露距离急剧下降，小于V相。

表2 V、W相暴露距离对比

山坡倾角V相暴露距离/mW相暴露距离/m5°10°15°20°25°30°35°40°3.419 73.410 73.394 53.357 23.095 12.418 41.141 003.850 33.742 33.513 23.091 92.378 81.237 000

4 结论

通过计算爬坡线路在不同山坡倾角下的平均高度、保护角和绕击率，分析可得：

a. 山坡倾角影响线路的平均高度，导线平均高度随着倾角的增大而减小，而且减小趋势明显。

b. 山坡倾角影响保护角计算值，上相保护角计算值随着倾角的增大而减小，中下相保护角计算值变化趋势则相反。

c. 山坡倾角的增大会降低线路遭到绕击的概率，但对于翻越山坡倾角大的线路，上相暴露距离最大，应加强上相的绝缘配置。

参考文献：

[1] DL/T 620-1997，交流电气装置的过电压保护和绝缘配合[S]．

[2] 钱冠军，王晓瑜，汪 雁，等．输电线路雷击仿真模型[J]．中国电机工程学报，1999，19(8)：39-44．

[3] 李瑞芳，吴广宁，曹晓斌，等．复杂地形输电线路绕击耐雷性能计算方法的改进[J]．高压电器，2011，47(4)：96-100．

[4] 李瑞芳，吴广宁，曹晓斌，等．山区输电线路雷电绕击跳闸率的计算[J]．电网技术，2010，34(12)：142-146．

[5] 程 勇，戴玉松，许 安．山区输电线路电气几何模型计算绕击率探讨[J]．四川电力技术，2005，28(4)：26-28，51．

[6] 孟遂民．架空输电线路设计[M]．北京：中国电力出版社，2007.

[7] Transmission and Distribution Committee of the IEEE Power Engineering Society．IEEE guide for improving the lightning performance of transmission lines[C]．New York：The Institute of Electrical and Electronics Engineers Inc，1997．

[8] 李瑞芳，吴广宁，曹晓斌，等．雷电流幅值概率计算公式[J]．电工技术学报，2011，26(4)：161-167．

[9] 苏红梅，郑雄伟，刘晓冬．雷电定位系统监测的河北省南部电网雷电流分布特征分析[J]．河北电力技术，2009，28(6)：1-3．