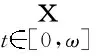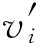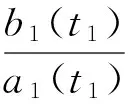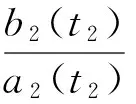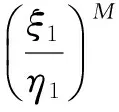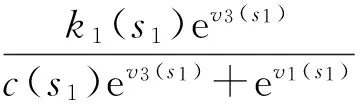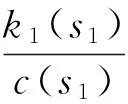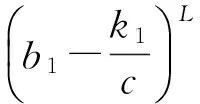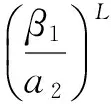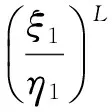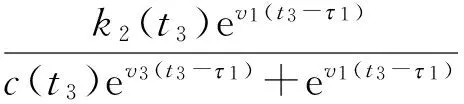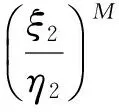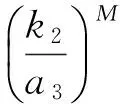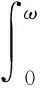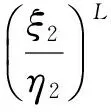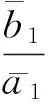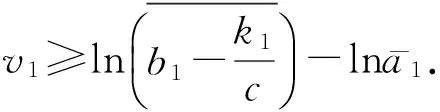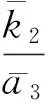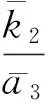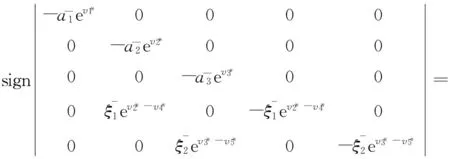一类具有斑块扩散与反馈控制的捕食者-食饵模型周期解的存在性

谢旺生,翁佩萱

(华南师范大学数学科学学院,广东广州 510631)

一类具有斑块扩散与反馈控制的捕食者-食饵模型周期解的存在性

谢旺生,翁佩萱*

(华南师范大学数学科学学院,广东广州 510631)

研究一类具有斑块扩散与反馈控制的捕食者-食饵模型,把微分方程求解问题转化为算子方程求解问题, 利用重合度的连续性定理证明了这一模型至少存在一个正周期解.

捕食者-食饵系统; 周期解;反馈控制; 重合度; Mawhin连续性定理

1 引言与预备知识

捕食-被捕食模型一直是种群生态学的一个十分基本和重要的研究模型. 由于人为或大自然的因素,野生动物的整个生存环境被铁路、公路、小岛等分割成许多斑块,形成斑块生态环境.越来越多的生物学和生理学证据表明,在许多情况下,特别是当捕食者不得不搜寻食物因而不得不分享或竞争食物时,一个更切合实际且更一般的捕食-被捕食模型应基于“比率依赖”理论,也就是说捕食者种群密度的平均增长率应该是食饵种群密度与捕食者种群密度之比的函数. 例如,XU 和 CHEN在文献[1]中讨论了2个斑块且功能性反应为Michaelis-Menten型的捕食者-食饵模型的持续生存和稳定性.

在生态模型中加入反馈控制项,是近20年来生态数学研究的一个课题,其意义在于人们能根据得到的信息来决定控制策略,进而进行相关的调整,使物种之间达到新的平衡.这个思想在以微分方程为模型的生态系统的体现最早来自GOPALSAMY和WENG的工作[2]. 自GOPALSAMY和WENG的工作之后,对于带有反馈控制项的不同生物模型,许多学者都做了不少研究工作[3-8].

考虑周期环境对生物系统的影响有理论和实际意义,启发我们对文献[1]中将周期系数函数引进反馈控制作捕食者之间的竞争以及反馈控制作用,从而得到了下面的生物模型：

(1)

其中,xi(t) (i=1,2)表示第i个斑块食饵种群在t时刻的密度,y(t)表示捕食者种群在t时刻的密度,bi(t),ai(t),ki(t),Di(t),ηi(t),ξi(t),βi(t) (i=1,2),c(t),r(t)都是以ω为周期的正连续函数,ω>0为常数. 考虑初始条件:

本文主要利用MAWHIN重合度理论中的连续性定理讨论系统(1)正周期解的存在性,相关理论和应用参考文献[9]-[10]. 下面首先给出一些关于重合度理论的基本概念和定理,这些知识将在后面的证明中用到.

设X,Z为赋范向量空间,L：DomL⊂X→Z为线性映射,N:X→Z为连续映射.称映射L为指标为零的Fredholm映射,如果满足dimKerL=codimImL<+∞并且ImL是Z中的闭子集. 如果L是指标为零的Fredholm映射,P：X→X,Q：Z→Z是连续的投影算子,使得 ImP=KerL, ImL=KerQ=Im(I-Q),并有X=KerLKerP,Z= ImLImQ.记Lp为L在DomL∩KerP上的限制,记Kp为Lp=L|Dom L∩Ker P的逆映射. 设Ω是X中的有界开集,如果QN(Ω) 和Kp(I-Q)N(Ω):Ω→X分别是Z和X的相对紧集, 则称N在上是L-紧的. 由映射L为指标为零的Fredholm映射可以推知,ImQ与KerL同构,故同构映射J： ImQ→KerL一定存在. 因为 ImQ⊆Z, KerL⊆X, 如果X=Z, 则可取J=I, 这里I是恒等算子.

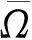
(a)Lx≠Nx,∀(0,1),x∂Ω∩DomL;

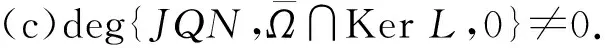
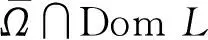
2 主要结果与证明

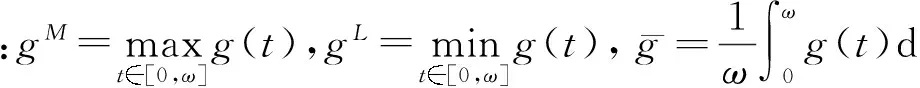
其中,

通过变换：x1(t)=ev1(t),x2(t)=ev2(t),y(t)=ev3(t),u1(t)=ev4(t),u2(t)=ev5(t),则系统(1)变为如下形式:

(2)

其中

f1(v(t),t)=b1(t)-a1(t)ev1(t)-

f2(v(t),t)=b2(t)-a2(t)ev2(t)-β1(t)ev4(t)+

D2(t)(ev1(t)-v2(t)-1),

f3(v(t),t)=-r(t)-a3(t)ev3(t)+

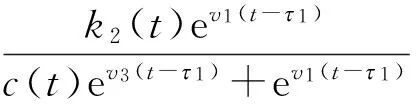
f4(v(t),t)=-η1(t)+ξ1(t)ev2(t-2)-v4(t),

f5(v(t),t)= -η2(t)+ξ2(t)ev3(t-3)-v5(t).

因此证明系统(1)有ω-正周期解(x1(t),x2(t),y(t),u1(t),u2(t))T,即转化为证明系统(2)有ω-周期解(v1(t),v2(t),v3(t),v4(t),v5(t))T.

L:DomL→Z,Lv=v′,

N:X→Z,

[Nv](t)=(f1(v,t),f2(v,t),f3(v,t),f4(v,t),f5(v,t))T,

P:X→X,v

Q:Z→Z,v

则有ImP=KerL, ImL=KerQ=Im(I-Q).

令Lp∶=LDom L∩Ker P. 通过简单计算,得到Lp的逆算子Kp: ImL→DomL∩KerP为:

因此

这里

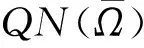
引理2 设参数(0,1),(v1(t),v2(t),v3(t),v4(t),v5(t))T是下面系统的一个ω-周期解

(3)

则有

|v1(t)|+|v2(t)|+|v3(t)|+|v4(t)|+|v5(t)|

其中

R1=G1+G2+G3,G1=2|lnR|+2|M1|,

(i=1,2,3,4,5),

则

(4)

由式(3)与式(4),得

fi(v(ti),ti)=0,fi(v(si),si)=0

(i=1,2,3,4,5).

(5)

若v1(t1)≥v2(t2),则v1(t1)≥v2(t1).由式(5)可得

D1(t1)(ev2(t1)-v1(t1)-1)

从而得到

(6)

若v1(t1)

a2(t2)ev2(t2)=b2(t2)-β1(t2)ev4(t2)+

D2(t2)(ev1(t2)-v2(t2)-1)

从而得到

(7)

由式(5)可得

从而得到

(8)

若v1(s1)≤v2(s2),则v1(s1)≤v2(s1).由式(5)可得

注意到假设(A1),有

(9)

若v1(s1)>v2(s2),则v1(s2)>v2(s2).由式(5)可得

a2(s2)ev2(s2)≥b2(s2)-β1(s2)ev4(s2)≥

b2(s2)-β1(s2)ev4(t4).

结合式(8),得

注意到假设(A2),有

(10)

由式(6)、(7)、(9)、(10),得

|v1(t)|+|v2(t)|<2|lnR|+2|M1|=∶G1.

(11)

由式(5)可得

结合式(9)与式(10),得

(12)

由式(8)和式(12),得

(13)

由式(5)可得

β2(t3)ev5(t3)

从而得到

(14)

由式(5)可得

(15)

结合式(14),得

(16)

对式(3)的第3个方程两边关于t从0到ω积分,可得

(17)

由式(15)和式(17),得到

(18)

由式(9)、(10)和式(14),得到

(19)

由式(18)和式(19)得

注意到假设(A3),得到

(20)

由式(3)的第3个方程及式(17),可得

(21)

由式(20)、(21)得到

特别地,

(22)

由式(5)及f5(v(t),t)的表达式可得

(23)

结合式(22),得

(24)

由式(14)、(16)、(22)和式(24),得到

(25)

(26)

则 |v1|+|v2|+|v3|+|v4|+|v5|≤R2,其中

(27)

(28)

|v1|≤N2, |v2|≤N2.

(29)

由式(26)的第3个方程,得到

(30)

由式(26)的第3个方程和式(26)的第5个方程,得

(31)

由式(27)、(28)和式(30),得

(32)

注意到假设(A3),由式(31)和式(32)得

(33)

由式(30)和式(33)得|v3|≤N3. 由式(26)的第4个方程和式(26)的第5个方程,并且结合式(29)与式(33),可得

(34)

定理1 设系统(1)满足假设(A1)～(A3),则系统(1)至少有一个ω-正周期解.

证明令

X:‖(v1(t),v2(t),v3(t),v4(t),v5(t))T‖<

R1+R2},

其中R1和R2由引理2和引理3所定义.下面关于系统(2),我们验证引理1的3个条件成立.

由于(a)和(b)显然，下面仅验证(c).

(c)作映射Φμ:DomL×[0,1]→Z,

deg(JQN,Ω∩KerL,(0,0,0,0,0)T)=

deg(Φ0,Ω∩KerL,(0,0,0,0,0)T).

由于下面代数方程系统

deg(JQN,Ω∩KerL,(0,0,0,0,0)T)=

至此,本文已经验证了引理1的3个条件在Ω上成立.因此,系统(2)至少存在一个ω-周期解,从而可知,系统(1)至少存在一个ω-正周期解.

[1] XU Ru, CHEN Lansun. Persistence and stability for two-species ration-dependent predator-prey system with time delay in a two-patch environment[J]. Comput Math Appl, 2000,40: 577-588.

[2] GOPALSAMY K, WENG Peixuan. Feedback regulation of logistic growth[J].J Math Sci, 1993,16:177-192.

[3] CHEN Xiaoxing, CHEN Fengde. Stable periodic solution of a discrete periodic Lotka-Volterra competition system with a feedback control[J]. Appl Math Comput, 2006, 181: 1446-1454.

[4] GOPALSAMY K, WENG Peixuan. Global attractivity in a competition system with feedback controls[J].Comput Math Appl, 2003,45: 665-676.

[5] LI Yongkun, ZHANG Tianwei. Permanence of a discrete n-species cooperation system with time-varying delays and feedback controls[J]. Math Comput Modelling, 2011, 53: 1320-1330.

[6] LIU Q, XU R. Persistence and global stability for a delayed nonautonomous single-species model with dispersal and feedback control[J]. Differential Equations Dynam Systems, 2003,11:353-367.

[7] WENG Peixuan. Existence and global stability of positive periodic solution of periodic integrodifferential systems with feedback controls[J]. Comput Math Appl,2000, 40: 747-759.

[8] YAN Jurang, LIU Guirong. Periodicity and stability for a Lotka-Volterra type competition system with feedback controls and deviating arguments[J]. Nonlinear Anal Real World Appl, 2011,74: 2916-2928.

[9] 黄燕革,姚晓洁,黄勇. 时间测度上具有Beddington- DeAngelis类功能反应和扩散的捕食系统的周期解[J]. 华南师范大学学报：自然科学版,2010(4):19-26.

[10] GAINES R E, MAWHIN J L. Coincidence degree and nonlinear differential equations[M]. Berlin:Springer-Verlag, 1977.

Keywords： predator-prey system; periodic solution; feedback control; coincidence degree; Mawhin’s continuation theorem

ExistenceofPeriodicSolutionforaPredator-PreyModelwithPatch-DiffusionandFeedbackControl

XIE Wangsheng, WENG Peixuan*

(School of Mathematics, South China Normal niversity, Guangzhou 510631, China)

A periodic predator-prey model with patch-diffusion and feedback control is studied. By changing the ordinary differential system into an operator equation and using Mawhin’s continuation theorem, the existence of at least one positive periodic solution for this model is proved.

2011-07-06

教育部高等学校博士学科点专项科研基金项目(20094407110001);广东省自然科学基金项目(10151063101000003)

*通讯作者，wengpx@scnu.edu.cn

1000-5463(2012)01-0042-06

O175.14

A

【责任编辑 庄晓琼】