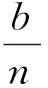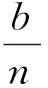一类非线性微分差分方程亚纯解的性质
2012-11-14彭长文陈宗煊
彭长文,陈宗煊
(1.华南师范大学数学科学学院,广东广州 510631; 2.贵州师范学院数学与计算机科学学院,贵州贵阳 550018)
一类非线性微分差分方程亚纯解的性质
彭长文1,2,陈宗煊1*
(1.华南师范大学数学科学学院,广东广州 510631; 2.贵州师范学院数学与计算机科学学院,贵州贵阳 550018)
利用值分布理论,研究了几类非线性差分方程是否有有限级超越亚纯解的问题,还考虑了“微分差分方程fn(z)+M(z,f)=h(z)是否存在有限级超越整函数解”的问题,其中n(≥3)是整数,h(z)是非零的有理函数,M(z,f)是关于f的线性微分差分多项式.
微分差分多项式; 差分多项式; 微分差分方程; 非线性差分方程
1 引言与结果
本文使用值分布理论的标准记号[1],用ρ(f)表示复平面上的亚纯函数f的级,m(r,f)表示均值函数,N(r,f)表示积分计数函数,T(r,f)表示f的特征函数.亚纯函数g是函数f的小函数是指:g满足T(r,g)=S(r,f)=o(T(r,f)),至多除去一个对数测度为有限的集合.
本文中,假设关于f的差分多项式是形如
其中亚纯系数b(J,J是一个有限指标集)满足T(r,b)=o(T(r,f)),μ(J,j=1,…,)是正整数且满足
并且至少有一个δ是非零的,n是P(z,f)的次数.
类似地,关于f的微分差分多项式是形如
其中亚纯系数b(J,J是一个有限指标集)满足T(r,b)=o(T(r,f)),μ(J,j=1,…,),nl,ni是不全为零的非负整数,且满足
ci,δ是复常数,n是Q(z,f)的次数.
假设f(z)是亚纯函数,定义
为f的e-型级.
近几年来,许多研究者对复差分进行了大量的研究,得到了许多有意义的结果[2-5].非线性差分方程的超越解的性质也一直受到关注,YANG和LAINE[6]对几类非线性差分方程解的增长性进行研究,并且得到如下定理.
定理A 假设q(z),p(z)是多项式且q(z)不恒为零,则非线性差分方程
f2(z)+q(z)f(z+1)=p(z)
没有有限级的超越整函数解.
定理B 若q(z)为非常数多项式,b,c为非零复常数,则方程
f3(z)+q(z)f(z+1)=csinbz
无有限级整函数解.如果q(z)=q是一个非零常数,当b=3n,q3=(-1)n+1c2,n是一个非零整数,则该方程有3个互相判别的有限级整函数解.
定理C 令n≥4是一个整数,M(z,f)是关于f的线性微分差分多项式,h是一个有限级亚纯函数.则微分差分方程
fn(z)+M(z,f)=h(z)
最多有一个有限级超越整函数解使得M(z,f)的系数是关于f的小函数.如果这个解存在,则f和h的级相同.
本文将以上几个定理的结果推广到更一般的情况,得到了如下结果.
定理1 假设n(≥4)是整数,q(z)是非零多项式,b,c为非零复常数,则非线性差分方程
fn(z)+q(z)f(z+1)=csinbz
(1)
无有限级的整函数解.
YANG和LAINE[6]考虑了n=3和q(z)是非常数多项式的情形,得到了定理B.而在本文中,讨论了当整数n≥4,q(z)是非零多项式的情形,得到了定理1,推广了定理B的结果.
定理2 假设q(z),p(z)是非零多项式,则非线性差分方程
f2(z)+q(z)f(z+1)=p(z)
(2)
无有限级超越亚纯解.若存在无穷级超越亚纯解,则σe(f)≥log 2.
定理3 假设c1,…,cm是非零复常数,m,n是正整数,且n≠m,q(z),p(z)是多项式且q(z)不恒为零,则非线性差分方程
fn(z)+q(z)f(z+c1)…f(z+cm)=p(z)
(3)
没有有限级的超越整函数解.
定理3精炼和推广了定理A.
定理4 若q(z)为多项式,p(z)为有限级超越整函数,则方程
f2(z)+q(z)f(z+1)=p(z)
(4)
的所有有限级超越亚纯解的级满足ρ(f)=ρ(p).
定理5 令n(≥3)是一个整数,M(z,f)是关于f的线性微分差分多项式,h是一个有理函数.则微分差分方程
fn(z)+M(z,f)=h(z)
(5)
没有有限级超越整函数解.
定理C研究了在h是亚纯函数的条件下,导出方程(5)至多有一个有限级的超越整函数解f,且ρ(f)=ρ(h).而定理5专门讨论若h是有理函数,则方程(5)无有限级的超越整函数解.
注1 当m=n时,方程(3)存在有限级超越整函数解.
例1 方程
f2(z)-f(z+1)f(z-1)=sin21
有解f(z)=sinz,ρ(f)=1.
当m≠n时,方程(3)可能存在无限级超越整函数解.
例2 方程
fn(z)-f(z+1)=0
有解f(z)=exp(ezlog n),ρ(f)=∞.
2 引理
为了证明定理,需要下面的引理.
引理1[7]若f是非常数的级为ρ<+∞的亚纯函数,则对于任意给定的复数c1,c2和任意的ε>0,有
成立.
引理2[7]若f是亚纯函数,其极点收敛指数()=<+∞,η≠0是一固定的复常数,则对任意的ε>0,有
N(r,f(z+η))=N(r,f)+O(r)+O(logr)
成立.
引理3[7]令f是一个级为ρ<+∞的亚纯函数,η是一固定的非零复常数,则对任意ε>0,有
T(r,f(z+η))=T(r,f)+O(rρ-1+ε)+O(logr).

有有限级的超越亚纯解,则d=max{p,q}≤n.

的差分方程,其所有系数的增长是o(T(r,y)) (r→∞),di不恒为零,并且假设y是该方程的非有理亚纯解,d=max{p,q}>n,那么对任意ε,0<ε<(d-n)/(d+n),存在r0>0使得当r≥r0有
其中C=max{|c1|,…,|cn|}和K>0是常数.
引理6[9]假设fj(z) (j=1,…,n;n≥2)是亚纯函数,gj(z) (j=1,…,n)是整函数,满足
(2)当1≤j 引理7[10]假设g:(0,+∞)→,h:(0,+∞)→是单调增函数,且在一个对数测度为有限的集合E外满足g(r)≤h(r),则对任意的α>1,存在r0>0,使得对所有r>r0,有g(r)≤h(αr)成立. 引理8[6]若c是一个非零常数,α是一个非常数亚纯函数.则微分方程f2+(cf(n))2=α没有超越亚纯解满足T(r,α)=S(r,f). 引理9[6]形如 H(z,f)P(z,f)=Q(z,f) 的微分差分方程,其中H(z,f),P(z,f),Q(z,f)是关于f的微分差分多项式,H(z,f)的最高次数是n,并且Q(z,f)的次数小于等于n.如果f是该微分差分方程的级为ρ<+∞的超越亚纯解,且H(z,f)只包含一项次数最大的项,则对任意ε>0,有 m(r,P(z,f))=O(rρ-1+ε)+S(r,f) 在一个对数测度为有限的集合外成立. 定理1的证明假设Q(z)是方程(1)的多项式解,则有 Qn(z)+q(z)Q(z+1)=csinbz. (6) 显然式(6)左边是多项式,而右边是超越整函数,所以方程(1)没有多项式解. 假设f是方程(1)的超越整函数解,对方程(1)两边微分有 nfn-1(z)f′(z)+q′(z)f(z+1)+ q(z)f′(z+1)=cbcosbz, (7) bfn(z)+bq(z)f(z+1)=bcsinbz. (8) 对式(7)、(8)两边平方相加有 f2n-2(z)[b2f2(z)+n2f′(z)2]=Tn+1(z,f), Tn+1(z,f)是关于f的次数小于等于n+1的微分差分多项式,其系数是多项式. 下面分2种情形讨论: (一)Tn+1(z,f)≡0时,有b2f2(z)+n2f′(z)2≡0,从而 T(r,b2f2(z)+n2f′(z)2)= m(r,b2f2(z)+n2f′(z)2)=S(r,f) 成立,进而由引理7知α=b2f2+n2f′2是关于f的不恒为零的小函数.由引理8可知α必是一个常数.对α=b2f2+n2f′2两边微分也有 解得 f(z)=l1eibz/n+l2e-ibz/n, 整理得 (9) 即 (10) 式(10)的所有系数是常数或是多项式. (11) 综上可知,当n≥4时,方程(1)不存在有限级的整函数解. 定理2的证明若f(z)是方程(2)的不具有极点的超越亚纯函数解,即f(z)是超越整函数.将方程(2)变形为 由p(z),q(z)是多项式,f(z)是超越整函数,有 T(r,p)=o(T(r,f)),T(r,q)=o(T(r,f)) (r→∞) 且d=max{2,0}=2>1=n,C=1,由引理5可知对任意ε,0<ε<(d-n)/(d+n)=1/3,存在r0>0使得当r≥r0有 其中K>0是常数,从而有 (12) 令ε→0有 若f(z)为方程(2)具有极点的超越亚纯函数解,设z0为f(z)的k阶极点,则z0+1为f(z)的2k阶极点,z0+2为f(z)的22k阶极点,…,z0+s为f(z)的2sk阶极点.从而 n(|z0|+s,f)≥2sk+O(1), logn(|z0|+s,f)≥slog 2+O(1), 则 综上可知σe(f)≥log 2. 注2 在定理2的证明过程中,如果f是方程(2)有极点的超越亚纯解时,也可直接应用引理5证明,过程和f是方程(2)的超越整函数解时的证明完全一样,从而定理2的证明可综合为上述证明过程中的第一部分. 定理3的证明当n>m时,有n=max{p,q}= max{n,0}>m,由引理4可知方程(3)无有限级超越整函数解. 当m>n时,由引理1和方程(3),有 mm(r,f)=m(r,fm)= m(r,fn)+O(rρ-1+ε)+O(logr)= nm(r,f)+O(rρ-1+ε)+O(logr). 因此 (m-n)T(r,f)=(m-n)m(r,f)≤ O(rρ-1+ε)+O(logr), 所以ρ(f)<ρ,矛盾. 综上可知,当m≠n时,方程(3)没有有限级的超越整函数解. 若考虑方程(3)是否存在有限级超越亚纯解,直接由引理4可得到下面的推论1. 推论1 假设c1,…,cm是非零复常数,m,n是正整数,n>m,且q(z),p(z)是多项式,q(z)不恒为零,则非线性差分方程 fn(z)+q(z)f(z+c1)…f(z+cm)=p(z) 没有有限级的超越亚纯函数解. 定理4的证明设f是方程(4)的级为ρ<+∞的超越亚纯函数解,则有 ρ(p)=ρ(f2(z)+q(z)f(z+1))≤ max{ρ(f2(z)),ρ(q(z)f(z+1))}=ρ(f). 从而ρ(p)≤ρ(f). 若ρ(p)<ρ(f),则存在σ使得ρ(p)<σ<ρ(f)=ρ,从而由方程(4)和引理3有 2T(r,f)=T(r,f2)=T(r,p(z)-q(z)f(z+1))≤ T(r,p)+T(r,f(z+1))+T(r,q)≤ T(r,f)+rσ+O(rρ-1+ε)+S(r,f). (13) 对所有充分大的r,式(13)在一个对数测度有限的集合外成立.当ε充分小时,由引理7可得 ρ(f)≤max{ρ-1+2ε,σ+ε}<ρ. 矛盾,所以ρ(f)=ρ(p). 定理5的证明若设f是方程(5)的级为ρ(f)=ρ<∞的超越整函数解,将方程(5)变形为 从而 T(r,h)+T(r,f)+O(rρ-1+ε)+S(r,f)= T(r,f)+O(rρ-1+ε)+O(logr)+S(r,f). 因此 (n-2)T(r,f)≤O(rρ-1+ε)+O(logr)+S(r,f). (14) 若ρ(f)=0,则有 (n-2)T(r,f)≤o(1)+O(logr)+S(r,f). (15) 若0<ρ(f)=ρ<∞,由h是有理函数可知ρ(h)=0.设0=ρ(h)<σ<ρ(f)=ρ,则 T(r,h)+T(r,f)+O(rρ-1+ε)+S(r,f)≤ T(r,f)+O(rρ-1+ε)+rσ+S(r,f). 因此 (n-2)T(r,f)≤O(rρ-1+ε)+rσ+S(r,f). (16) 由式(16)导出ρ(f)<ρ矛盾. 综上可知方程(5)不存在有限级的超越整函数解. [1] HAYMAN W K. Meromorphic functions[M]. Oxford: Clarendon Press, 1964. [2] HALBURD R G, KORHONEN R J. Difference analogue of the lemma on the logarithmic derivative with applications to difference equations[J]. J Math Anal Appl, 2006,314(2): 477-487. [3] LAINE I, YANG C C. Clunie theorems for difference andq-difference polynomials[J]. J Lond Math Soc, 2007, 76(2): 556-566. [4] CHEN Z X, HUANG Z B, ZHENG X M. On properties of difference polynomials[J]. Acta Mathematica Scientia,2011: 1-7. [5] HALBURD R J, KORHONEN R J. Nevanlinna theory for the difference operator[J]. Ann Acad Sci Fenn Math, 2006,31: 463-478. [6] YANG C C, LAINE I. On analogies between nonlinear difference and differential equations[J]. Proc Japan Acad: Ser A, 2010, 86:10-14. [7] CHIANG Y M, FENG S J. On the Nevanlinna characteristic off(z+η) and difference equations in the complex plane[J]. Ramanujan J, 2008, 16(1): 105-129. [8] HEITTOKANGAS J, KORHONEN R J, LAINE I, et al. Complex difference equations of Malmquist type[J]. Comput Methods Funct Theory, 2001,1: 27-39. [9] YANG C C, YI H X. Uniqueness theory of meromorphic functions[M].Dordrecht: Kluwer Academic Publishers Group, 2003. [10] GUNDERSEN G. Finite order solutions of second order linear differential equations[J]. Trans Amer Math Soc,1988,305:415-429. Keywords: difference-differential polynomial; difference polynomial; difference-differential equation; nonlinear difference equation PropertyofMeromorphicSolutionsofCertainNonlinearDifferentialandDifferenceEquations PENG Changwen1,2, CHEN Zongxuan1* (1.School of Mathematics,South China Normal University,Guangzhou 510631, China;2.School of Mathematics and Computer Sciences, Guizhou Normal College, Guiyang 550018, China) By applying Nevanlinna’s value distribution theory of meromorphic functions, the following problems are investigated: the existence of finite order transcendental meromorphic solutions of several kinds nonlinear difference equations, and the existence of finite order transcendental entire function solutions of differential-difference equations with the formfn(z)+M(z,f)=h(z), wheren(≥3) is an integer,h(z) is a given non-vanishing rational function, andM(z,f) is a linear differential-difference polynomial inf. 2010-12-14 国家自然科学基金项目(10871076) *通讯作者,chzx@vip.sina.com 1000-5463(2012)01-0024-05 O174.52 A 【责任编辑 庄晓琼】
3 定理的证明