用展开法求正则长波方程的新解
2012-11-14曾玉婷
曾玉婷,陈 浩
(华南师范大学物理与电信工程学院,广东广州 510631)
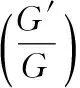
曾玉婷,陈 浩*
(华南师范大学物理与电信工程学院,广东广州 510631)
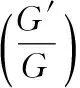
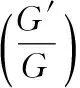
BENJAMIN等[1]在1971年提出了正则长波方程(Regularized-Long-Wave Equation),简称RLW方程:
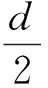
(1)
其中a,b,d为常数.
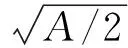
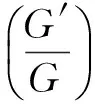
通过行波变换u(x,t)=u(ξ),ξ=x-Vt,方程(1)可化为
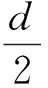
(2)
其中u′=uξ=du/dξ.积分一次,得到
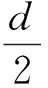
(3)

m+2=2m.
(4)
可得m=2.
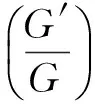
(5)
其中G(ξ)满足二阶常微分方程,
G″+G′+μ=0,
(6)
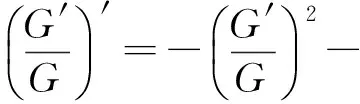
(7)
由式(7)易得
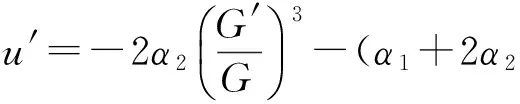
(2α2μ+α1
(8)
及
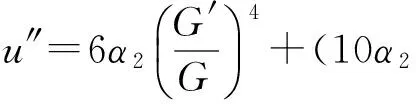
(8α2μ+3α1
(2α1μ+6α2μ.
(9)
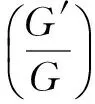
常数项:
Va(2α2μ+μα1
(10)

(11)
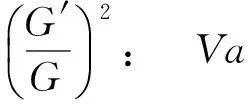
(12)
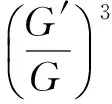
(13)
(14)
解由式(10)~(14)组成的方程组可得
(15)
此时代回式(5)可以得到方程(1)的形式解:
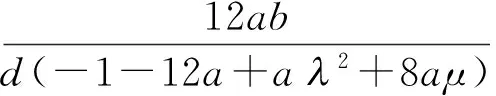
(16)
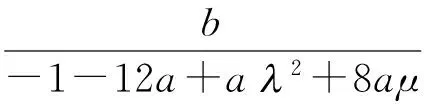
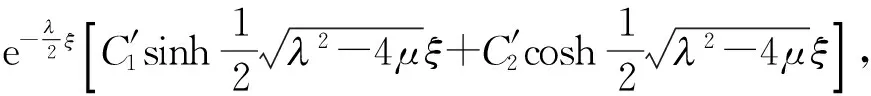
(17)
所以
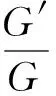
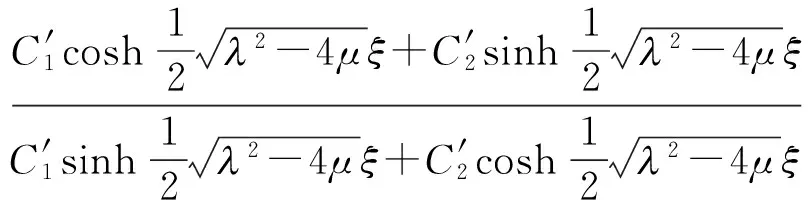
(18)
代回式(16)可得方程的解,则


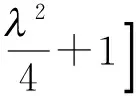
(19)
这是一个新的孤子解.
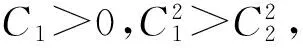
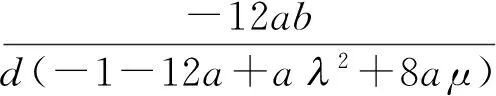
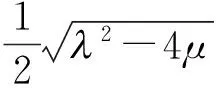
(20)
与文献[9]作比较,即RLW方程中系数取为a=β,b=-1,d=-α,此时式(20)变为:
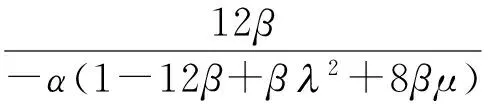
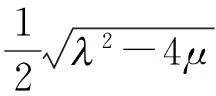
(21)
在文献[9]中当p=2时方程由推广的RLW方程变成RLW方程,它的解为:

(22)
解(21)与解(22)在形式上都是sech2解,只是,μ等系数可以取不同的值,这说明求出新的孤子解(19)在满足的条件下,可以变形得出经典解.图1是取一定的初始条件时的孤子解(19)的图像.

图1 钟形孤子解
按孤子稳定性的论证[10],可以证明孤子解(19)在受到小扰动时,孤子的能量和波形、波速都是稳定的.
G=e(cosξ+sinξ),
(23)
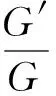
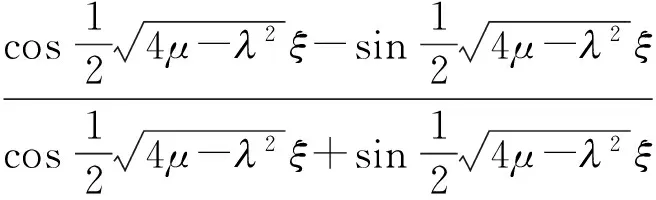
(24)


(25)
这是一个周期解.方程的图像如图2所示,从图中可以看出这是一个周期解,不是孤子解.
G=e(C1+C2ξ).
(26)
则
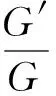
(27)

(28)
这是有理式解,解的图像如图3所示,易知解(28)的能量是不稳定的,在受到小扰动后波形会发生变化,不是稳定解.所以此解并无特殊意义.

图2 周期解
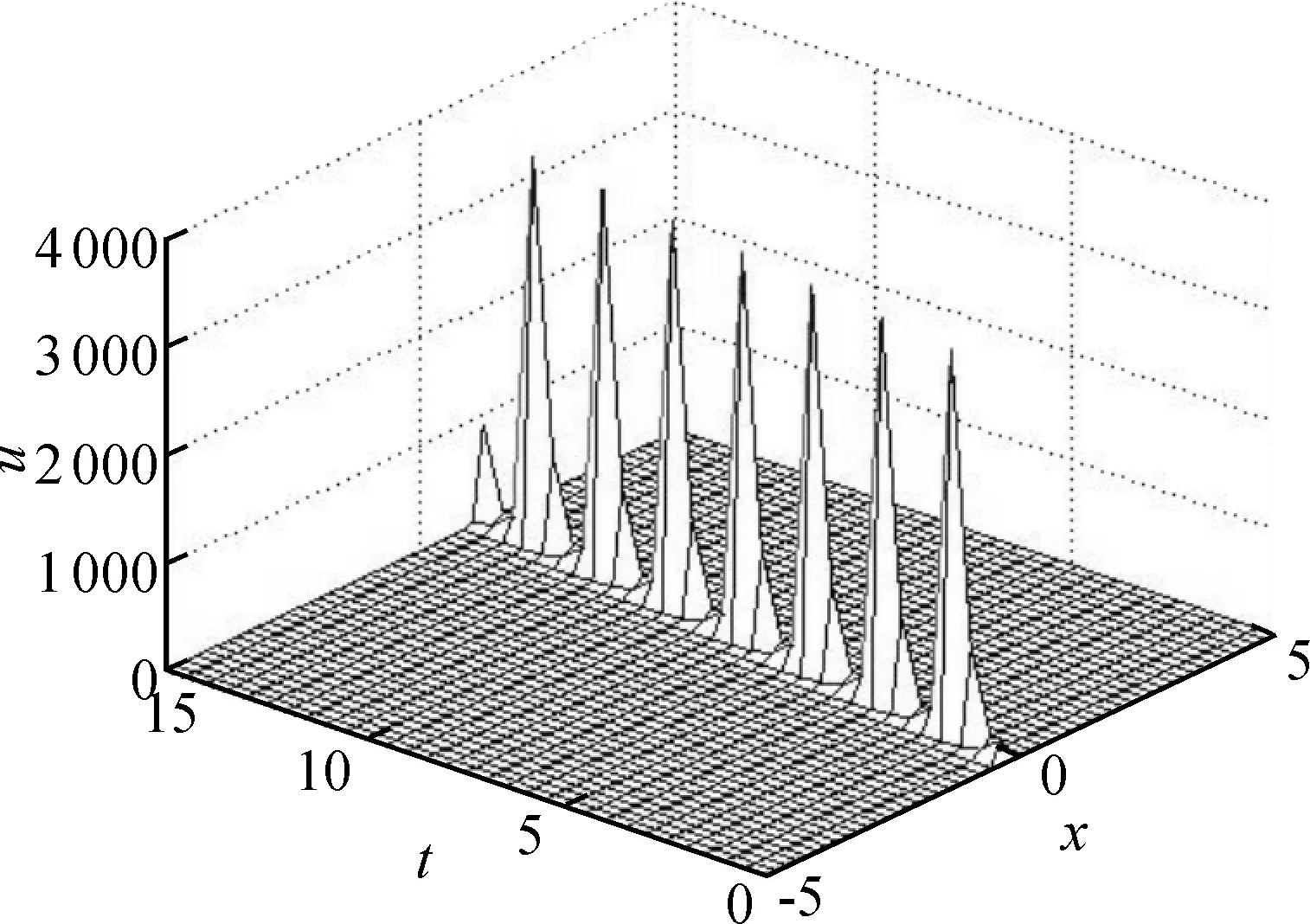
图3 有理式解
2 结论
[1] BENJAMIN T B,BONA J L,MAHONY J J.Model equations for long waves in nonlinear dispersive systems[J].Phill Trans R Soc Lond A,1972,272:47-78.
[2] MORRISON P J,MEISS J D,CAREY J R.Scattering of RLW solitary waves[J].Physica,1984:324-336.
[3] YAN C T.Regularized long wave equation and inverse scattering transform[J].Phys,1993,24:2618-2630.
[4] BEKIR A.New exact travelling wave solutions for regularized long-wave,phi-four and Drinfeld-Sokolov equations[J].Int J Nonlinear Sci,2007,6:46-52
[5] LEWIS J C,TJON J A.Resonant production of solitons in the RLW equation[J].Phys Lett A,1979,73: 63-72.
[6] RASLAN K R.A computational method for the regularized long wave (RLW) equation[J].Appl Math Comput,2005,167(26):1101-1118.
[7] 李志斌.非线性数学物理方程的行波解[M].北京:科学出版社,2007.
[8] WANG M L,LI X Z,ZHANG J L.The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics [J].Phys Lett A,2008,372:417.
[10] 庞小峰.孤子物理学[M].重庆:重庆科技出版社,2000.

ZENG Yuting,CHEN Hao*
(School of Physics & Telecommunication Engineering,South China Normal University,Guangzhou 510631,China)
2011-03-18
*通讯作者,chenhao@scnu.edu.cn
1000-5463(2012)01-0072-04
O481.3
A
【责任编辑 庄晓琼】
