高强混凝土框架结构延性性能数值模拟分析

巩玉发，张殊赫

（辽宁工程技术大学 建筑工程学院，辽宁 阜新 123000）

随着科技的发展，高强混凝土结构得到越来越广泛的应用。高强混凝土具有强度高、变形小、早强等特点，能大幅提高结构的承载能力，可减小构件的截面尺寸，减轻结构自重，满足工程经济、高效的需求[1]。但混凝土随着强度的提高，其变形能力迅速降低，脆性性能明显。因此，对高强混凝土结构，应在充分发挥高强度优势的同时，提高其变形能力，满足工程要求。研究表明，通过适当配筋可使构件及结构具有足够的延性，满足地震区的抗震设防要求。

《建筑抗震设计规范》中抗震设防目标为“小震不坏，中震可修，大震不倒”。建筑物在大震作用下是否倒塌，不取决于其承载力的大小，而在于其延性是否满足抗震要求。因此，地震区的建筑应设计为延性结构而具有很好的抗震性能。

文章采用伯克利大学研发的DRAIN-2DX程序对12层2跨的高强混凝土框架结构进行非线性数值模拟分析，深入探讨其延性性能。

1 高强混凝土框架结构的延性

钢筋混凝土框架结构作为一种常见的结构形式，广泛地应用于抗震设防地区[2]。它具有平面布置灵活，整体性好，足够的强度和良好的延性等优点。对于框架结构来说，足够的强度和良好的延性是保证结构具有良好抗震性能的两个主要因素。钢筋混凝土框架结构中的框架柱中采用高强混凝土，可提高其承载能力、减小截面尺寸，减轻自重。同时，经合理的设计，结构应具有足够的变形能力和耗能能力。特别是在大震作用下，通过部分结构构件的破坏来耗散地震能量，避免结构倒塌。

1.1 延性的概念

延性是指结构，构件或构件的某个截面从屈服开始到达最大承载能力或到达以后而承载能力还没有明显下降期间的变形能力[3－7]。延性通常包括截面、构件和结构三个层次。其中，结构延性称为总体延性，构件延性则称为局部延性，两者密切相关。结构的总体延性是通过构件的延性来实现的，但这并不意味着若结构中含有高延性构件，其总体延性就一定高。若设计不合理，即使结构中有些构件的延性很高，其总体延性却未必好。两者之间的关系和塑性铰形成后的破坏机制有关。构件延性由截面延性决定。虽然已对延性问题作了大量科研工作，但目前仍不能精确地定量描述几者之间的关系，故规范只能根据工程经验、试验结果或理论分析等通过构造措施来保证结构具有足够的延性。延性反映了结构在大变形下吸收和耗散地震能量的能力，同时，也降低了结构的刚度，使其在地震作用下反应减小。对于钢筋混凝土框架结构来说，在地震作用下，要求其处于完全弹性状态既不现实也无必要。在地震作用下，允许结构的薄弱构件首先屈服，出现塑性铰，降低刚度，可增大塑性变形能力。当结构的塑性铰达到一定数量时，整体结构就会出现屈服现象，结构的变形迅速增加。延性结构就是指能够维持足够的承载能力而又有较大塑性变形能力的结构。

结构延性具有如下作用：

1）可防止构件发生脆性破坏；

2）可承受偶然作用的影响；

3）可实现塑性内力重分布；

4）更有利于结构抗震。

1.2 影响延性的因素

钢筋混凝土框架结构由梁、板、柱以及节点组成。其中整体框架结构的延性由梁、柱及节点的延性来决定。

1.2.1 影响梁延性的主要因素 梁的截面尺寸；梁的纵筋配筋率和配筋形式；剪压比；梁端箍筋加密。

1.2.2 影响柱延性的主要因素 混凝土强度等级；柱的截面形状；柱的轴压比；柱的剪跨比；柱的纵向钢筋配筋率；柱的箍筋形式及配箍率。

1.2.3 影响节点延性的主要因素 剪压比；轴压比；水平箍筋和竖向箍筋。

1.3 保证延性的措施

为了增强结构在遭遇罕遇地震时的抗倒塌能力，结构应具有较高的延性，通过耗能使结构振动迅速衰减。构件的延性同其受力状态、配筋量及配筋方式有关，一般可采取下列措施来提高构件延性：减小竖向构件的轴压比；减小梁的受压区高度，尽量使梁的受压与受拉配筋比较接近；“强剪弱弯”，避免剪切破坏先于弯曲破坏；尽可能避免短柱；加强梁端、柱端的箍筋，避免混凝土压溃先于纵筋屈服；加强梁 柱节点区，避免节点破坏先于构件破坏；柱箍筋采用螺旋箍；加强钢筋锚固，避免钢筋锚固的粘结破坏先于构件破坏；对预埋件也应避免锚固破坏先于连接件破坏。

2 高强混凝土本构关系

在对高强混凝土结构进行数值模拟分析时，材料本构关系决定模拟结果是否精确。文章对高强混凝土框架结构平面体系进行非线性数值模拟分析，采用单轴受力材料，满足计算精度、非线性分析等要求。由于高强混凝土是一种脆性材料，由多种材料复合组成，力学性能较复杂，离散性较大，目前仍没有一个公认的本构关系模型。

2.1 高强混凝土受压时本构关系曲线

（1）OA 段曲线：

式中，σi为混凝土受压时的主应力；E0为混凝土初始弹性模量；Es为峰值应力割线模量；σic为σ－εiu曲线上第i主应力方向上的峰值应力；εic为对应σic的应变，一般取0.002。

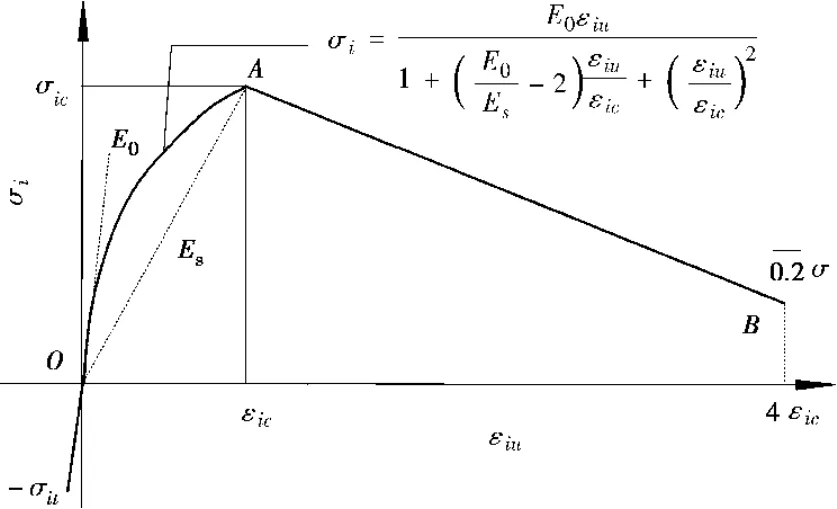
图1 高强混凝土受压应力 应变曲线

（2）AB段曲线：

上述公式反映了高强混凝土在受压时下降段的缓急程度，随着混凝土强度等级的提高，下降段参数α迅速增大，说明其下降段的斜率增大，反映了高强混凝土随着强度的增加延性减小，脆性增大的特点。

2.2 高强混凝土受拉时本构关系曲线

高强混凝土受拉时其应力的增加并没有受压时那么明显，故其应力－应变曲线通常采用受拉上升段和水平直线段组成。关于受拉下降段，大多没有加以考虑。即将混凝土在受拉屈服后理想化为一段水平塑性段，其应力保持不变，当拉应变超过εtu后应力降为零。

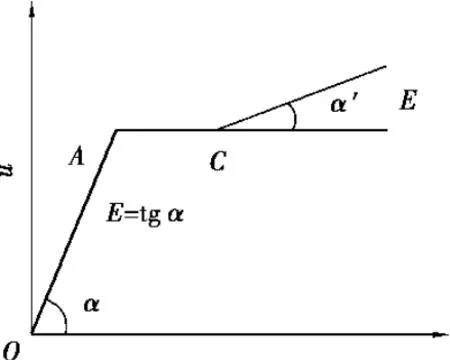
图2 高强混凝土受拉应力 应变关系

3 高强混凝土框架结构数值模拟分析

笔者应用伯克利大学研发的DRAIN-2DX程序对高强混凝土框架进行数值模拟分析。以12层2跨高强混凝土框架结构作为模型，跨度均为6.0m，除底层高度为4.6m外，其余各层层高均为3.0m。计算时将其简化为平面体系，取一榀框架作为计算单元。计算简图如图3所示。模型1～8层柱截面尺寸为500mm×500mm，9～12层柱截面尺寸为450mm×450mm，主梁截面尺寸均为250mm×450mm，柱混凝土强度等级为C80，梁混凝土强度等级为C30，梁、柱中纵筋均采用HRB400级。地震波选用1940年的EL-centro波（峰值为341.7Gal），地震加速度记录如图4所示。

3.1 最大位移和最大层间位移

图3 计算模型

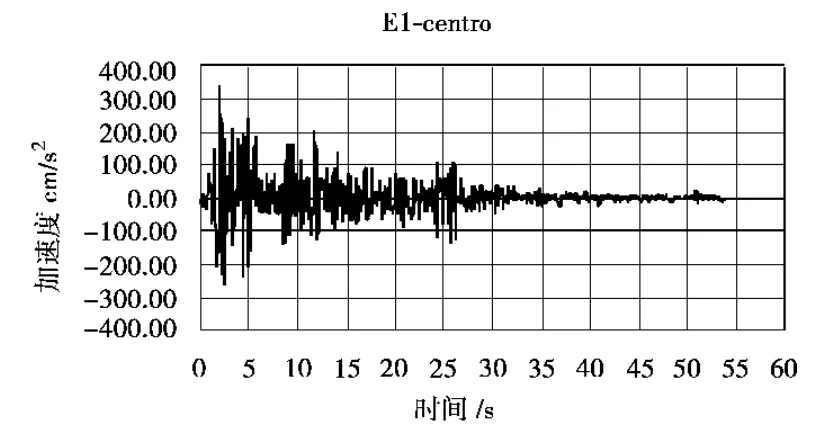
图4 EL-centro地震波原始记录图

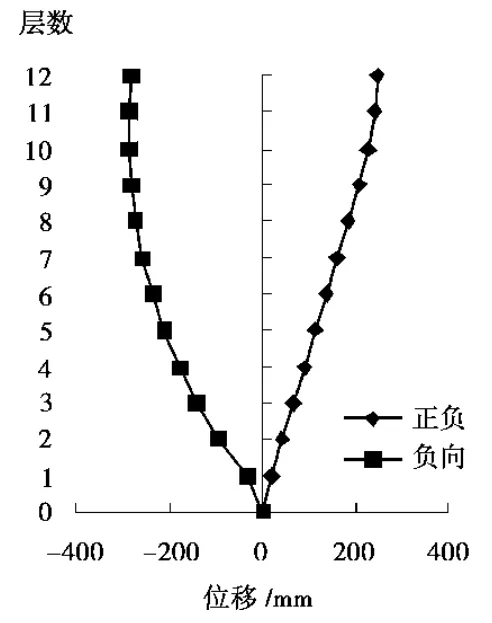
图5 El-centro波作用下结构各层最大位移

由上述图5-6可知：高强混凝土提高了柱底控制截面的屈服水平，减小结构出现软弱首层破坏的可能性，有效的克服了底层的薄弱现象；负向位移明显比正向位移大很多，说明当结构屈服时产生较大的不可恢复变形，导致结构在偏离主轴方向震动；负向层间位移角最大值为0.188，小于《建筑抗震设计规范》规定的关于钢筋混凝土框架结构弹塑性层间位移角限值1／50，避免框架柱形成塑性铰，避免倒塌机构的形成；具有很好的变形滞回耗能能力。

3.2 位移时程曲线

上述反应只是最大值反应，这不能看到反应的全貌，为此下面给出时程曲线。通过时程曲线的比较，可清楚的看到高强钢筋混凝土框架结构的地震反应总体上比普通钢筋混土框架结构小。

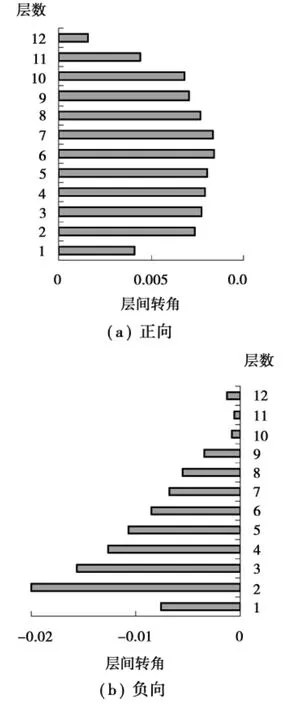
图6 EL-centro波作用下结构各层层间位移

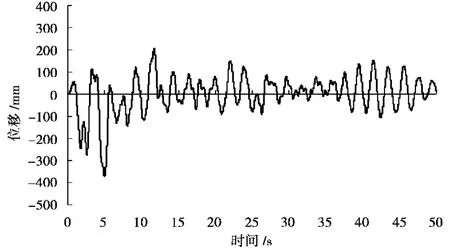
图7 EL-centro波作用下模型结构顶层位移时程曲线

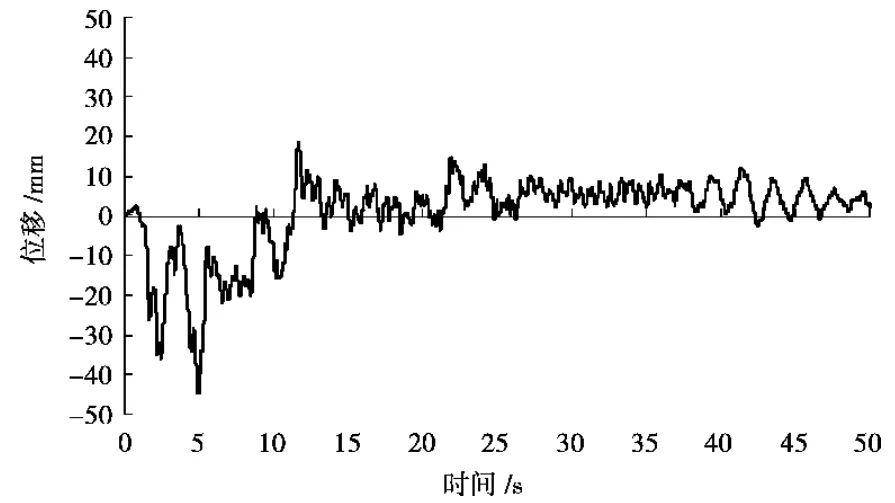
图8 EL-centro波作用下模型结构底层位移时程曲线

图7-8分别为在EL-centro波作用下模型结构顶层和底层位移时程反应曲线，由顶层位移时程曲线可看出模型结构大体在主轴附近振动，无明显偏移现象，说明在顶层并没有产生塑性铰；由底层位移时程曲线可看出，时程曲线明显偏离初始平衡位置，这是因为底层柱在经历地震作用的峰值后产生塑性铰，使结构整体向一边偏斜，不能恢复到原来的位置。

4 结 论

文章应用DRAIN-2DX程序对高强混凝土框架进行非线性反应数值模拟分析，探讨了高强混凝土框架结构在地震作用下延性性能，得出以下结论：

（1）在地震作用下，结构的延性性能是决定其抗震性能的重要指标。

（2）通过合理的设计，高强混凝土框架结构能够具有较好的延性满足抗震地区的塑性变形要求。

（3）DRAIN-2DX程序可很好地模拟高强混凝土框架结构的破坏过程及耗能能力。

（4）模型结构底层的位移时程曲线发生了偏离初始平衡位置的现象，此现象加剧了结构的二阶效应，对抗震十分不利，今后需对此情况作进一步研究。

[1]王丽娟.高强钢筋高强混凝土框架结构非线性模型研究[J].山西建筑，2007，33（12）：60-62.WANG Lijuan.Research on nonlinear mechanical of high strength reinforced concrete RC frame [J].Shanxi Architecture，2007，33（12）：60-62.

[2]陈滔，黄宗明.钢筋混凝土框架非弹性地震反应分析模型研究进展[J].世界地震工程，2002，18（1）：91-97.CHEN Tao，HUANG Zongming.A review of inelastic dynamic analysis models of reinforced concrete frames under earthquake ground motions[J].World Information on Earthquake Engineering，2002，18（1）：91-97.（in Chinese）

[3]林建煌.从中日抗震设计方法的不同，浅谈钢筋混凝土结构的延性设计[J].福建建筑，2011，156（6）：52-54.LIN Jianhuang.Ductility design of reinforced concrete structure with comparing Sino-Japan aseismatic design[J].Fujian Architecture ＆ Construction，2011，156（6）：52-54.

[4]蔡健，周靖，方小丹.钢筋混凝土框架抗震位移延性系数研究[J].工程抗震与加固改造，2005，27（3）：2-6.CAI Jian，ZHOU Jing，FANG Xiaodan.Study on seismic Displacement Ductility Factor of Reinforced Concrete Frame Structure[J].Earthquake Resistant Engineering and Retrofitting，2005，27（3）：2-6.（in Chinese）

[5]王克海，李茜，韦韩.国内外延性抗震设计的比较[J].地震工程与工程振动，2006，26（3）：70-73.WANG Kehai，LI Qian，WEI Han.Comparing overseas and inland specifications for ductility seismic design[J].Earthquake Engineering and Engineering Vibration，2006，26（3）：70-73.（in Chinese）

[6]罗文斌，钱稼茹.特征延性系数谱及RC框架的目标位移[J].建筑结构，2004，34（10）：24-26.

[7]于洋.延性设计对框架结构抗震能力的改善[J].科学技术与工程，2009，24（9）：7551-7553.YU Yang.The improvement to sismic capacity of the frame structure by means of ductility design[J].Science Techno logy and Engineering，2009，24（9）：7551-7553.