ANFIS实现依据人数变化来预测建筑负荷

涂方亮，吴静怡

（1.上海交通大学 机械与动力工程学院，上海 200240；2.上海交通大学 上海 200240）

商场人员分布和流动是建筑物内部负荷变化的重要影响因素。一些物理隔断将其分成不同的专卖店，每个隔断区域中人员的进出和逗留时间的长短是随机变化的。在室外环境一定的情况下，由于商场运营期间，各个隔断的灯光及营业员所产生的负荷基本是不变的，商场隔断区域的空调负荷直接由顾客的流动而引起变化，如促销、品牌和其它因素将导致局部区域顾客的分散和集中，直接导致隔间负荷明显或大或小。

通常，人员热扰产生的空调负荷是由人体散热量来计算的[1]，而传统的室内空调设定温度和换气效率均是以整个空调房间为考虑对象，而人员活动区域只占空调房间的一部分，因此不考虑人员的需求而将整个房间作为研究对象所创造的微气候不一定对人最为有利，同时也导致很大的能量需求。考虑到以上的影响，文献[2]中提出了反映了使用者在室内停留的性质和方式。既描述某一个人在房间各处的时间分配状况，也可以描述房间内所有人员在房间各处的总时间分配关系。目前，红外光电检测技术是比较成熟的技术[3]，可以利用商场里红外光电设备的客流计数器跟踪人员的用途，来直接调控局部空调的负荷变化，以适应人员的随机变动和逗留的影响自适应神经模糊系统（ANFIS）[4]是一种基于数据的建模方法，该系统中的模糊隶属度函数及模糊规则是通过对大量已知数据的学习得到的，而不是基于经验或直觉任意给定的。文献[5]首先提出了ANFIS的定义，它结合了模糊系统和神经网络的最优特征。近几年已经应用于很多领域。文献[6]采用模糊神经方法预测一定条件下房间的温度，证实ANFIS对预测的可靠性；文献[7]提出一种基因算法和ANFIS的混合模型，结果表明混合模型更加准确地预测建筑能源；文献[8]通过使用ANFIS和神经网络训练数据集来调整隶属函数和相关参数；文献[9]阐释ANFIS在地源热泵系统中的应用；文献[10]采用ANFIS可以准确快速地预测HVAC系统的风阀调节。

本文采用ANFIS模型实现依据人员数量和逗留时间来预测和控制空调实时负荷。

1 自适应神经模糊系统（ANFIS）

为了后面实例的应用，在模糊推理系统中设定两个输入量（x，t）和一个输出量u。此处一阶T－S型模糊推理被设定为[11]：

规则i：If（xis Ai）and（t is Bj），then ui＝f（x，t）＝aix＋bit＋ci其中，Ai和Bj模糊集合，ui是通过模糊规则后的输出量，ai，bi和ci是训练过程中被确定的设计参数。该系统通常由下列层数组成：

第一层：在输入向量中每个节点和每个部件（xi和ti）直接连接，它的主要作用是将输入值传送到下一层。

第二层：每个节点代表着一个语言变量，如 N3、N2、N1、Z、P1、P2、P3。它的作用是计算出隶属度函数，即（x）和（t），i＝1，2，…，n；j＝1，2，…，n。

该层还用来匹配模糊规则前件，计算出每条规则的适应度（αk）。

i＝1，2，…，n；j＝1，2，…，n；k＝1，2，…，m。

第三层：该层有m个节点，每个节点代表一个规则，它的作用是实现归一化。

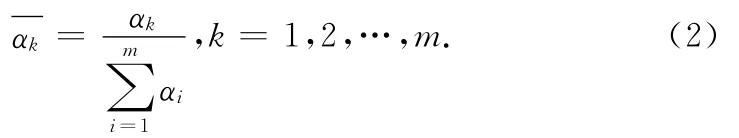
第四层：该层也有m个节点，每个节点显示一条规则，它用来计算每个规则的后件。这样，输出量如下：

第五层：这个节点计算ANFIS的整体输出量。u是规则的加权和，加权系数是模糊规则的归一化适应度，即

2 实例研究与建模

2.1 研究对象的描述

为了阐释ANFIS依据人员数量和逗留时间来预测隔间实时负荷方面的应用，本文选择商场中净面积为33.6m2的隔间区域作为研究对象，依据隔间的人员数量指标及人员作息模式通过DEST-c计算其相应冷负荷值作为基础数据集，时间区间为6月15日到10月15日，人均产热量为168W，人均产湿量0.2kg／h。经调研，该区域中人员最少为2人（营业员），最多人数为90人；且每个人员在商场大多数区域中滞留时间约3min，在不同区域中滞留的时间不超过20min。

2.2 模型的基础数据集

商场顾客随机移动着，随着时间的变化，每个区域中的顾客数量也在不停的变化。根据该区域实际所能存在的情况（包括人数及其可能存在的逗留时间），计算得到其最大冷负荷为32.23kW，最小冷负荷为2.88kW，故本文结合实际调研结果，并在此限定的负荷区间中随机地选取了300组数据，基本涵盖了该隔间区域日常运行中所能产生的负荷数据。

2.3 模型的建立

本文以区域人员的数量和逗留时间作为ANFIS模型的输入量，其输出量为隔间对应的最大冷负荷。根据已知数据集，采用减聚类方法的模糊推理系统，该方法是由文献[12]提出的山峰聚类法的改进，是一种用来估计一组数据中的聚类个数以及聚类中心位置的快速单次算法。图1是实例中两个输入量在减聚类法下输出的聚类中心。从而，在给定的数据集和减聚类方法下，系统模型结构简图如图2所示。该方法明显对ANFIS模型有着预处理的作用，在一定的聚类半径下所选的输入量x和t均聚类成七个模糊子集，使得控制更加简单化。其中，x指人员数量；t指顾客的逗留时间，单位为min；u指计算的实时最大冷负荷，单位为kW。

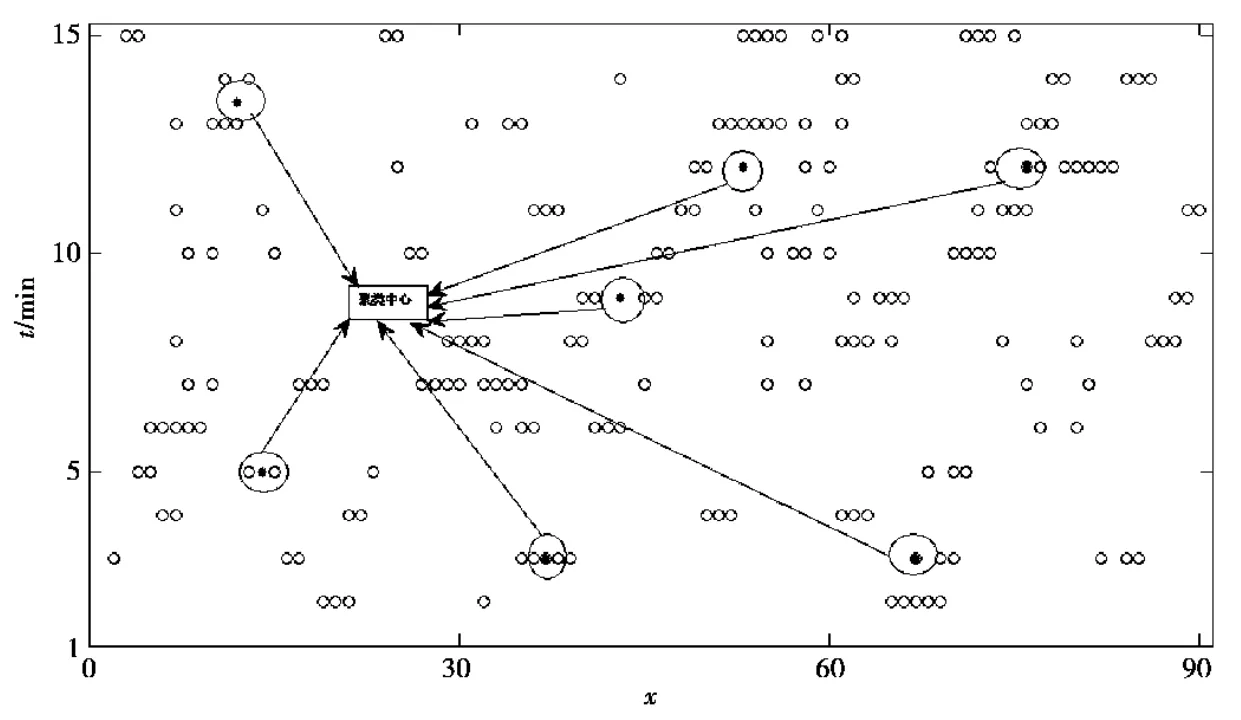
图1 减聚类法输出聚类中心

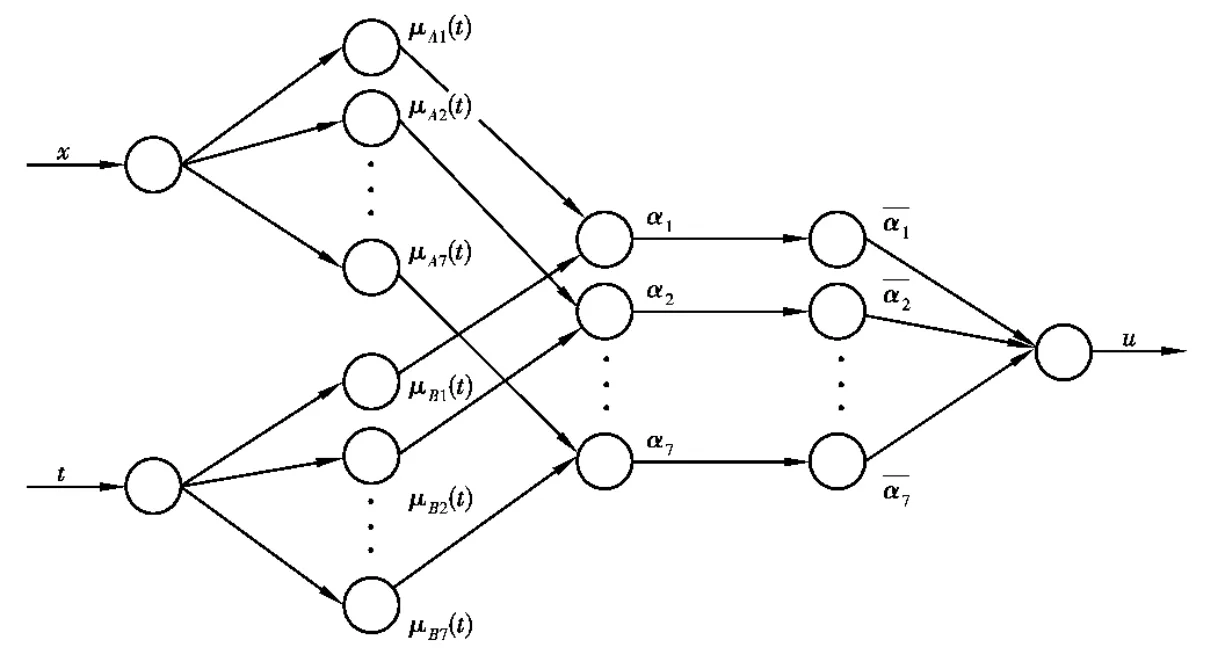
图2 减聚类法ANFIS模型结构简图

3 模拟结果

利用已获得的数据集并选定隶属函数，在 MATLAB2011b环境下，使用ANFIS模型进行模拟。除了平均误差外，还采用了可决系数（R2）来评估模型的有效性。

可决系数被定义如下[13－14]

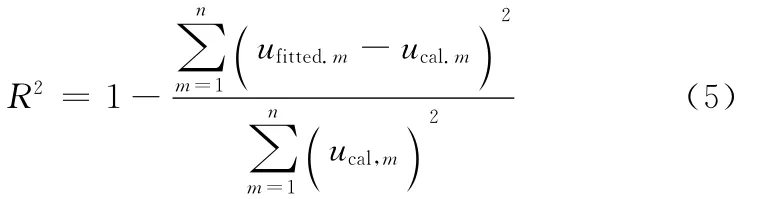
式中：ucal，m指计算值，ufitted，m指 ANFIS模型拟合值，n指样本数量。

3.1 模拟过程

300组数据被分成三个独立的子集：训练子集，核查子集和测试子集。首先，训练子集被重复使用来建立网络和调节网络结构的权重。接着，核查子集用来模拟已建模型的性能，以核实模型的通用性和适应性，最优的模型将被选做后期的使用。最后测试子集被用于检测模糊推理系统的结果通用性性能[15]。通常，三个子集的选用比例对模拟结果是有影响的，此处三种比例被设定进行比较，见表1。

目前，顾客区域分布和滞留仍然没有一个确切的函数分布，因此，在模拟过程中几种典型的隶属函数分别被选用并结合混合方法训练误差。当迭代300次时，不同类型的输出结果见表1。其中Gaussmf为高斯隶属函数；Gauss2mf为两高斯组合隶属函数；Trapmf为梯形隶属函数；Gbellmf为钟形隶属函数。

3.2 分析与讨论

从表1定性分析，采用类型1的ANFIS模型（Gauss2mf）结构可以获得满意的结果和准确的预测，其平均误差均最小。

基于Gauss2mf的ANFIS模型结果与原始计算值绘制在图3中，从而可以直观的看到随机抽取的300组数值结果之间的偏离度。在这个模型中，区域负荷处于最低状态下，数据组计算值和拟合值的误差绝对值为0.18，误差百分比绝对值为最大值5.3%；区域负荷处于最高状态下，数据组计算值和拟合值的误差绝对值为0.49，误差百分比绝对值为1.5%。而图4中，计算值和拟合值的趋势线显示其可决系数（R2）非常接近1，很明显本文减聚类法形成的模型是合适可行的。进而，在限定的范围内，随机选取两组数据（x1＝46，t1＝8；x2＝6，t2＝10）输入到模型中，可以获得相应的预测结果为u1＝17.3，u2＝4.1。而通过理论计算所获得的相应结果分别为17.5和3.96。二者结果相对误差在工程中明显可以接受，也足以证实模型的正确合理性。

因此，实时的输入量就可以获得准确的拟合输出量，进而可以实现人员的数量和逗留时间与隔间负荷的预测和调控。

表1 不同类型的ANFIS模型的性能

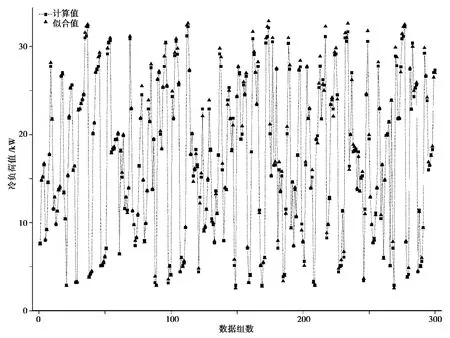
图3 ANFIS模型结果的比较

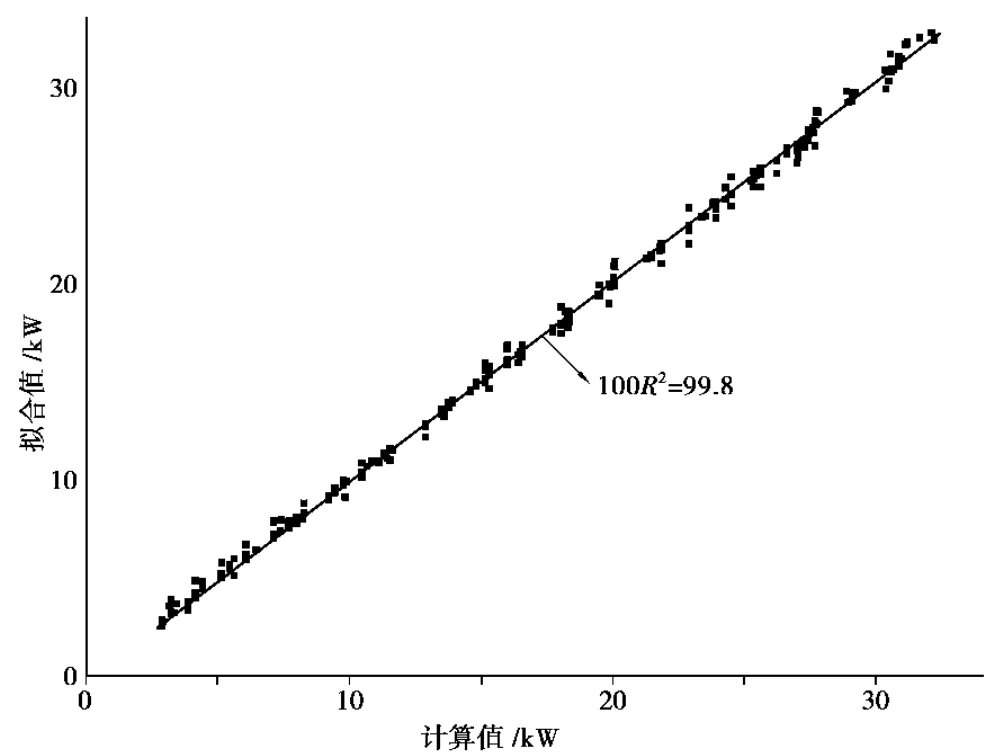
图4 ANFIS模型的性能评估

4 结 论

基于ANFIS模型，用于预测和控制商场隔间区域中不同人数所产生的实时冷负荷。可以获得以下结论：

（1）本文阐述了运用ANFIS模型实现依据人员的数量和逗留时间来控制和预测隔间实时冷负荷的可行性。以人员的数量和逗留时间作为输入量，隔间的实时最大冷负荷为输出量，采用Gauss2mf的ANFIS模型获得最优的结果，其预测值与计算值的平均误差最小，表明ANFIS模型用来预测区域冷负荷是可行及实用有效的，其准确程度达99.8%。

（2）在模拟过程中，人数与逗留的隶属函数选用了四种不同的常用函数，表1中的结果显示Gauss2mf在性能上优于其它隶属函数，从而在特定的条件下可以确定商场中人数的分布服从两高斯函数的组合（Gaussian 2）分布。

（3）在3.2节中，通过随机抽取的输入量，来核实预测结果和理论计算结果，验证了模型的正确合理性。同样，本次确定的最终模型也适用于上海类似的其它商场隔间区域，且其冷量近似在2.88kW和32.23kW之间。而对于不在特定范围内的其它商场类建筑，则一样可以采用本文的方法进行具体的设定。

[1]李先庭，赵彬著.室内空气流动数值模拟[M].北京：机械工业出版社，2009.

[2]Zhao B，Li X.Revised air-exchange efficiency considering occupant distribution in ventilated rooms[J].Journal of the Air ＆Waste Management Association，2003，53（6）：759-763.

[3]Ezaki H，Nambu T，Nincmiya R，et al.Estination of liquidus temperature of Sn-basecd alloys and its application to the design of Pb-free solder[J].Journal of Materials Science：Materials in Electronics.2002，13（5）：269-272.

[4]石辛民，郝整清.模糊控制及其 MATLAB仿真[M].北京：清华大学出版社，2008.

[5]Jang J S R.Self-learning fuzzy controllers based on temporal back propagation[J].IEEE Transactions on Neural Network，1992，3（5）：714-723.

[6]Alasha'ary H，et al.A neuro-fuzzy model for prediction of the indoor temperature in typical Australian residential buildings[J].Energy and Buildings，2009，41：703-710.

[7]Li K J，et al.Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system：A comparative study[J].Energy and Buildings 2011，43：2893-2899.

[8]Wu J D，Hsu C C，Chen H C.An expert system of price forecasting for used cars using adaptive neuro-fuzzy inference[J].Expert Systems with Applications，2009，36：7809-7817.

[9]Ying L C，Pan M C.Using adaptive network based fuzzy infer-ence system to forecast regional electricity loads[J].Energy Conversation and Management，2008，49：205-211.

[10]Servet S.An expert system for the humidity and temperature control in HVAC systems using ANFIS and optimization with Fuzzy Modeling Approach[J].Energy and Buildings，2009，41：814-822.

[11]李国勇.神经模糊控制理论及应用[M].北京：电子工业出版社，2009.

[12]Yager R，Filev D.Generation of fuzzy rules by mountain clustering[J].Journal of Intelligent ＆ Fuzzy Systems，1994，2（3）：209-219.

[13]Hikmet E，Mustafa I，et al.Modelling aground-coupled heat pump system using adaptive neuro-fuzzy inference systems[J].International Journal of Refrigeration，2008，31：65-74.

[14]Sencan A，Kalogirou S A.A new approach using artificial neural networks for determination of the thermodynamic properties of fluid couples[J].Energy Convers.Manage.2005，46（15-16）：2405-2418.

[15]Chang F J，Chang Y J.Adaptive neuro-fuzzy inference system for prediction of water level in reservoir[J].Advances in Water Resources，2006，29：1-10.