不同热源位置下室内自然对流换热数值模拟

2012-11-14常建国薛思浩杨琳琳

土木与环境工程学报 2012年2期

常建国，薛思浩，杨琳琳

（辽宁工程技术大学建筑工程学院，辽宁阜新 123000）

自然对流换热问题是计算流体力学与数值传热学研究的重要课题之一，研究自然对流换热问题对改善室内空气环境、节约建筑能耗、抑制有害物扩散等具有重要的理论和现实意义[1]。1983年，De Vahl Davis G[2]对封闭方腔内的自然对流换热问题进行了研究，并发表了关于封闭方腔自然对流换热问题的基准解。Ben Yedder[3]、Bilgen[4]、Basak[5]等对方腔侧壁呈线性变化的自然对流换热模型进行了数值研究。国内汤广发[6]、李光正[7]、马洪林[8]等人先后对二维方腔内自然对流换热问题进行了不同方法的数值计算分析。

以上文献并没有涉及室内热源问题，笔者采用有限容积数值方法对质量守恒方程、能量守恒方程[9－10]进行离散求解，分析了在热源位置不同、不同Ra数的情况下，室内流体温度场、流场分布特征和Nu数的变化特征，为进一步研究室内自然对流换热过程提供一定的理论基础和参考数据。

1 数值计算

1.1 模型建立

物理模型[11－12]如图1所示。边长为H×H，房间屋面坡度θ＝30°，室内为空气，考虑重力影响，Pr＝0.71。底部中心位置有一内热源，尺寸为l×s（设a＝l／L，b＝s／L，本例取a＝0.1，b＝0.2），温度为Th，房间的左右壁面保持低温Tc，屋顶及地面除去热源的部分均为绝热。

计算网格采用非均匀网格划分[13]，靠近壁面处加密以满足精度要求[14]。为验证网格数对计算结果的影响，增加网格总数10%及20%，计算得到结果偏差均在1.0%之内，说明采用的网格具有独立性。

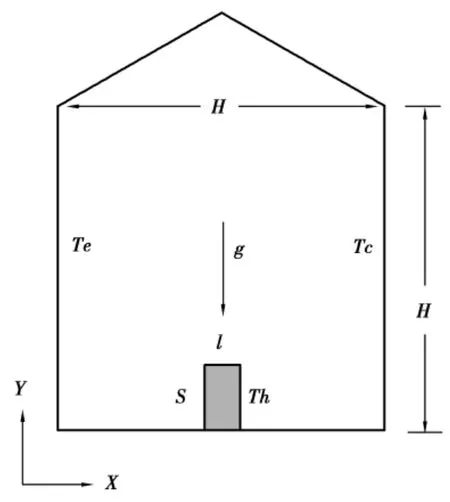
图1 物理模型

1.2 控制方程

为简化分析，做如下假设：将空气流动视为层流、稳态、不可压缩；室内空气热物性为常数，密度随温度的变化遵循Boussinesq假设。则该问题的无量纲控制方程[15]为

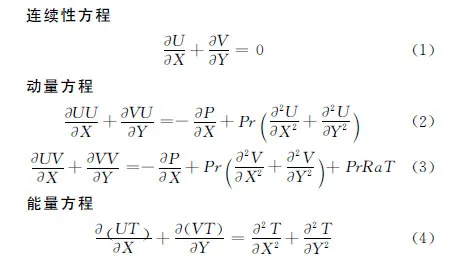
控制方程中采用的无量纲变量分别定义为

无量纲几何参数：（X，Y）＝（x，y）／H；

无量纲速度：（U，V）＝（u，v）H／α；

无量纲压力：P＝p／ρ（α／H）2；

无量纲温度：

上述方程中，H、α／H、ΔT分别作为长度、速度、温度的特征尺度进行无量纲参数化。此外，引入Prandtl数Pr、Rayleigh数Ra作为无量纲控制参数，分别定义为：，，其中υ为运动粘滞系数，α为导温系数。

1.3 物性参数

所采用物理参数为：参考温度为300K，Pr＝0.71，Th＝305K，Tc＝295K，β＝0.00333，υ＝1.589×10－5m2／s，α＝2.724×10－5m2／s，ρ＝1.1766kg／m3，μ＝1.8754×10－5N·s／m2，重力加速度g＝9.807m／s2。

1.4 数值求解

计算了Ra为103～106时封闭室内自然对流情况[16]。采用控制容积法（FVM）进行离散，压力速度耦合方程采用SIMPLE算法[17]；压力差值方案选择标准格式，动量和能量方程均采用二阶迎风格式；压力和动量欠松弛因子分别采用0.3和0.25[18]。

2 结果与讨论

2.1 等温线与流线特征

图2为Ra＝103～106，热源处于中间位置时的温度场和流场图。从图中可以看出，室内温度场和流场随着Ra的变化而变化。对于温度场，在Ra＝103时，等温线以热源为中心向外扩散呈拱形，靠近壁面处多为竖直方向，说明此时的传热机理主要以导热为主。在Ra＝104时，以内热源所在界面为对称面，温度场等值线开始发生弯曲变形，即逐渐由竖直方向向水平方向变化。随着Ra的增大，变形逐渐明显，对流换热作用逐渐增强。当Ra增大到106时，冷壁面附近的温度等值线几乎保持垂直，形成薄边界层，说明此时的换热机理为对流换热。对于流场，从图中可以看出，所有流场的共同点为：在底部热源浮升力的作用下，气流先从热源中部向上运动，后在房间左、右壁面处向下运动，整个流场由两个对称反向的涡旋组成。随着Ra的增大，两个涡旋也逐渐增大并变成椭圆，涡旋的中心逐渐上升向房间顶部靠拢。

由上述分析可知，存在热源的封闭房间在低温壁面处会产生边界层，较大的温度梯度会使人产生不舒适感，建议工作人员避免在墙壁区域工作。在高Ra数时，房间地面和冷壁面的交汇处会形成漩涡死角，易造成污染，应注意清洁。

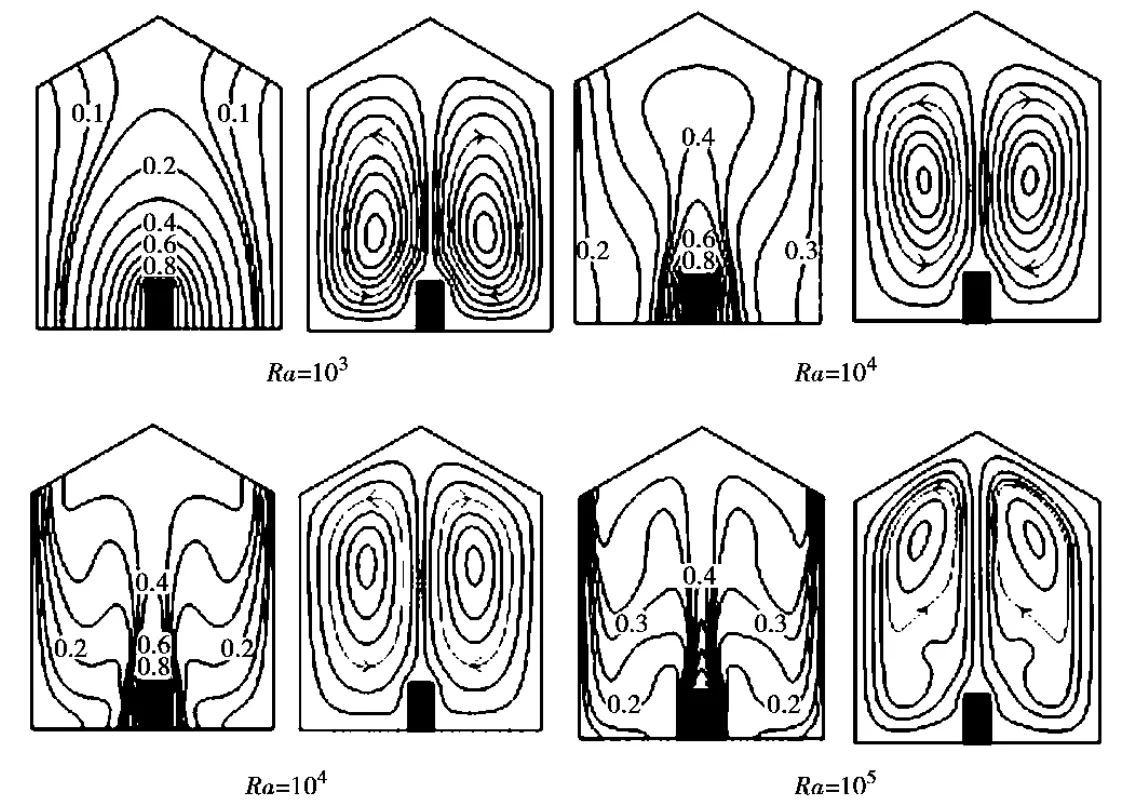
图2 D＝0.5时不同Ra下的温度场和流场图

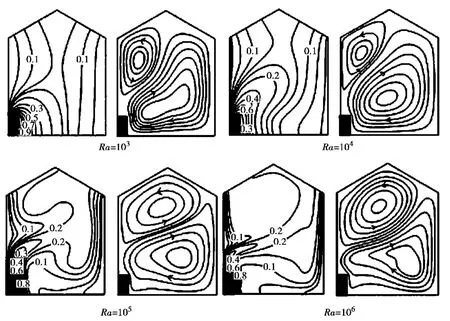
图3 D＝0时不同Ra下的温度场和流场图

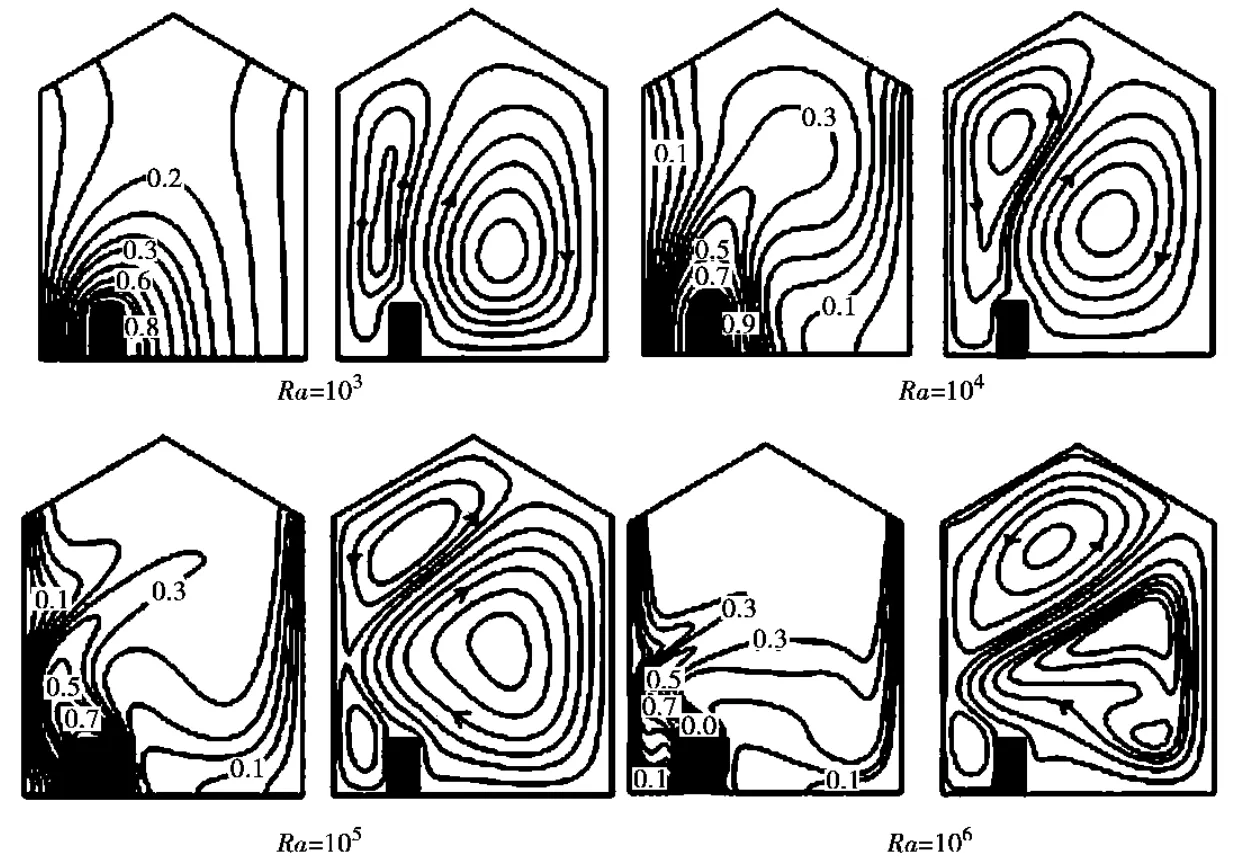
图4 D＝0.25时不同Ra下的温度场和流场图

2.2 Nu数的变化特征

Nu数随Ra数的变化关系如图5所示。将不同Ra数、不同热源位置下计算出的Nu数进行比较，可以看出，不同D值下，Nu与Ra数的关系曲线形状大致相同，均为以Ra为自变量的幂指数函数，拟合的线性相关性可达90%。D＝0.5时的曲线最陡，D＝0时的曲线最平缓，D＝0.25与D＝0.752种情况下Nu曲线几乎重合，只是在Ra＝106时有较小的差值。当Ra＝103时，D＝0与D＝1两种情况下Nu最大，这是由于2种情况下的热源位置都在壁面附近，虽然此时的室内传热以热传导为主，但仍然存在较弱的热对流形式，而热源只与一侧空气接触，故对流换热阻力较小，Nu值相对较大。随着Ra的增大，室内的对流换热越来越强烈，与空气接触的热壁面无量纲场地增大，Nu值也必然增大。

将5种情况下的Nu与Ra数进行拟合，得到的公式如表1所示。

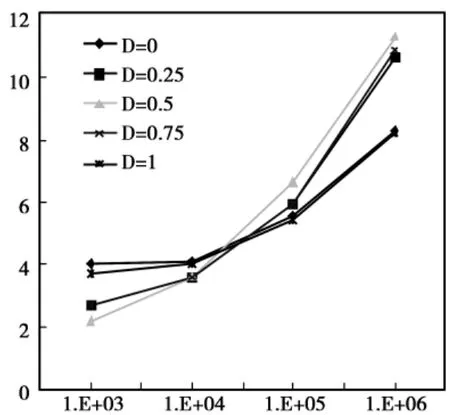
图5 不同热源位置下Nu随Ra的变化

表1 不同热源位置时的Nu数公式

3 结论

Ra＝103时，等温线以热源为中心呈均匀拱形向外扩散，靠近热源位置的温度梯度较大，随着Ra数的增加，传热由热传导向热对流转变，等温线逐渐弯曲变形，在冷壁和热壁附近形成薄边界层。

Ra＝103时，流线呈现为两个反向对称的涡，涡的大小与热源位置有关。随着Ra增大，热源上方的涡逐渐增大且有向上的运动趋势。D＝0.25情况下分裂为3个涡。

Ra＝103时，D＝0与D＝1，2种情况下的Nu最大。Nu数与Ra数呈幂数关系，拟合的线性相关性可达90%，符合理想效果。

热源的位置对换热量的影响较大，D＝0.5时Nu数曲线最陡，D＝0时曲线最平缓。

存在热源的封闭房间在低温壁面处会产生边界层，较大的温度梯度会使人产生不舒适感，建议工作人员避免在墙壁区域工作；在高Ra数时，房间地面和冷壁面的交汇处会形成漩涡死角，易造成污染，应注意清洁。

[1]赵福云.室内空气多态模拟及对流反演[D].长沙：湖南大学，2008.

[2]De Vahl Davis G，Jones I P.Natural Convection of Air in a Square Cavity[J].Int.J.Numerical Methods in Fluids，1983（3）：249-264.

[3]E.Bilgen，R.Ben Yedder.Natural convection in enclosure with heating and cooling by sinusoidal temperature profiles on one side[J].Int.J.Heat Mass Transfer，2007 （50）：139-150.

[4]E.Bilgen.Natural convection in cavities with a thin fin on the hot wall[J].Int.J.Heat Mass Transfer，2005（48）：3493-3505.

[5]T.Basak，S，Roy，A.R.Balakrishnan.Effects of thermal boundary conditions on natural convection flows within a square cavity[J].Int.J.Heat Mass Transfer，2006（49）：4525-4535.

[6]汤广发，陈在康，吕文瑚，等.二维层流室内自然对流数值解[J].空气动力学学报，1986（4）：407-414.

[7]李光正，马洪林，张宁.原始变量法计算封闭腔内自然对流[J].华中科技大学学报，2004，21（2）：4-7.

[8]马洪林.封闭腔内高瑞利数（Ra）层流与湍流自然对流数值模拟[D].武汉：华中科技大学，2004.

[9]杨世铭，陶文铨.传热学[M].4版.北京：高等教育出版社，2006.

[10]章熙民，任泽霈，等.传热学[M].北京：中国建筑工业出版社，2001.

[11]李光正，李贵，张宁.封闭腔内自然对流数值研究[J].华中科技大学学报：城市科学版，2002，19（4）：20-22.

[12]马洪林.封闭腔内高瑞利数（Ra）层流与湍流自然对流数值模拟[D].武汉：华中科技大学，2004.

[13]傅德薰，马延文.计算流体力学[M].北京：高等教学出版社，2002.

[14]杨伟，孙跃，薛思浩，等.射流混水过程数值研究[J].水资源与水工程学报，2010，21（5）：72-75.

[15]王福军.计算流体动力学分析[M].北京：清华大学出版社，2004.

[16]江帆，黄鹏.Fluent高级应用与实例分析[M].北京：清华大学出版社，2008.

[17]Pantankar S V.Numerical heat transfer and fluid flow[J].McGraw Hill，New York，1980.