全伺服驱动二自由度九杆机构的同步控制研究
2012-11-13黄海波莫健华杜二虎华中科技大学材料成形与模具技术国家重点实验室湖北武汉430074
黄海波,莫健华,吕 言,杜二虎(华中科技大学 材料成形与模具技术国家重点实验室,湖北 武汉 430074)
全伺服驱动二自由度九杆机构的同步控制研究
黄海波,莫健华,吕 言,杜二虎
(华中科技大学 材料成形与模具技术国家重点实验室,湖北 武汉 430074)
提出了一种二自由度九杆传动机构的全伺服驱动模式,运用MSC.ADAMS软件建立了该机构的虚拟样机模型,并在此基础上进行了同步控制的仿真。仿真数据显示,当两曲柄同步转动时,仅改变其彼此间的初始相位差,就可以获得多种形式的滑块运动曲线,曲柄2相对于曲柄1的初始相位差超前则滑块运动曲线理想,但扭矩增加;反之则扭矩降低,但滑块运动曲线却不是很理想。
机械设计;二自由度九杆机构;同步控制;初始相位差;伺服压力机
1 引言
传统精压机的传动机构一般采用单台普通电机通过齿轮啮合来同步驱动二自由度九杆机构,以输出满足工艺要求的行程曲线。然而,这样的精压机一旦结构尺寸和参数确定了,滑块的工艺行程曲线也就随之确定了,用户无法改变。
近年来,随着伺服电机和伺服控制技术的发展,在传统压力机的基础上开发新型的伺服压力机,已经逐渐成为一种主流和热潮[1][2]。
Yan Hongsen等[3]在Watt压力机的基础上利用伺服电机代替普通电机驱动其传动机构,开发出了新型的伺服压力机。Yossifon S和Shivpuri R[4]等以伺服电机驱动双曲柄连杆机构为研究对象,开发出了新型的双肘杆式伺服压力机。本文提出,在传统精压机传动机构的基础上,用两台伺服电机代替普通电机,全伺服驱动二自由度九杆机构。在同步控制研究中,仅改变两台电机的初始角相位差,就可获得多种形式的滑块运动曲线,实现了用户在现场可任意改变滑块运动规律的柔性化。构,形成全伺服控制的九杆机构。
如图1所示,该传动模型主要由平面铰链五杆机构ABCDE、曲柄滑块机构OFGJ和连杆CF组成。曲柄AB由伺服电机1驱动,作顺时针方向转动;曲柄ED由伺服电机2驱动,作逆时针方向转动。为了改善压力机滑块的受力条件,取L5、L6成一条直线时作为滑块位置的上死点TDC(Top Dead Center),且上死点为压力机滑块的工作点。取滑块的上死点作为滑块位移的起点,BDC(Bottom Dead Center)为滑块位移的下死点。
采用下传动布局,是考虑到滑块在回程过程中,即由上死点向下死点运动时,可以充分利用整个机

2 二自由度九杆机构的运动模型
根据文献[5]中的瑞士GKP系列传统精压机九杆机构传动模型,建立如图1所示的全伺服驱动二由度九杆机构模型。该模型与前者的区别在于:前者一般采用单台普通电机通过齿轮传动同步驱动二自由度九杆机构,而本文提出一种去掉齿轮传动机构,用两台伺服电机分别驱动两曲柄将动力输入连杆机构的重力作用,实现快速回程,同时可以降低电机的回程扭矩。且下传动的方案,使机构布局紧凑,便于安装和实现。
3 九杆机构的虚拟样机模型
在机械系统仿真分析软件MSC.ADAMS中建立其虚拟样机模型,如图 2 所示[5]~[7]。
图1与图2中,各杆件的结构尺寸如表1所示。
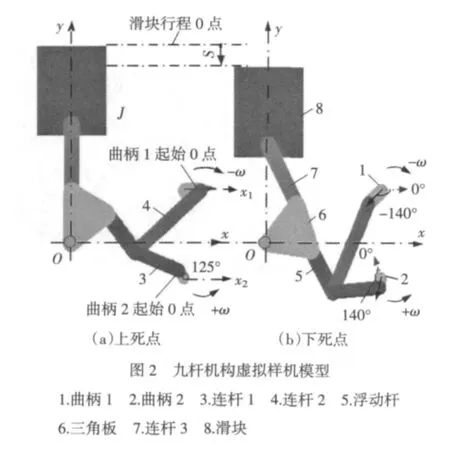
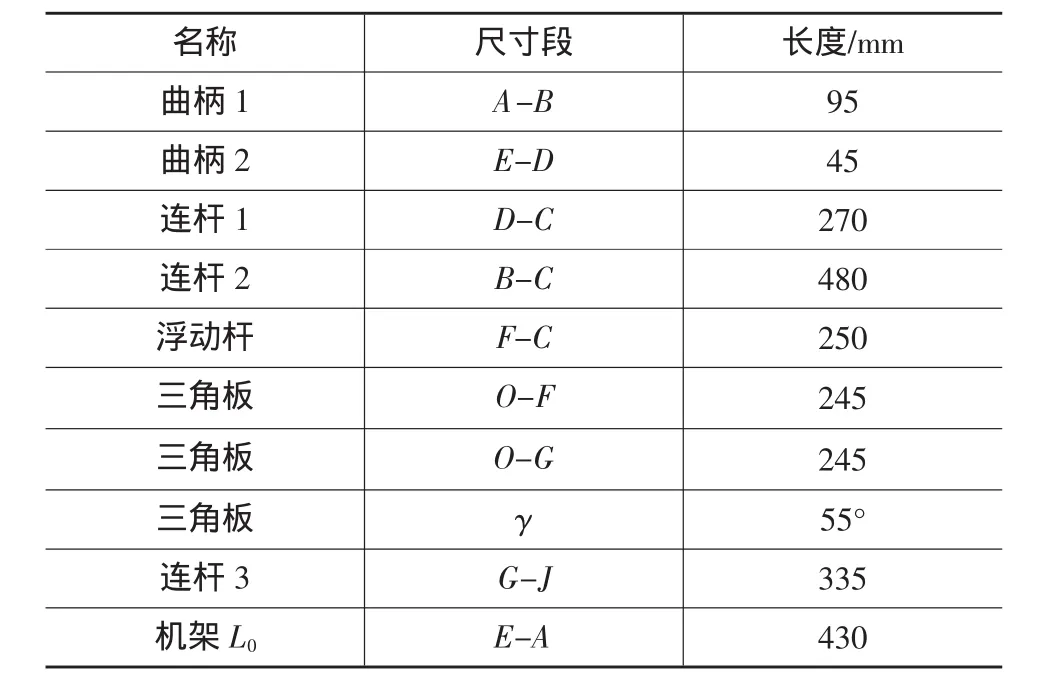
表1 各杆件的结构尺寸
3.1 样机模型初始化定义
(1)如图2a所示,在样机模型中,把曲柄1的初始位置设在水平轴x1上,定义为曲柄1转角的起始点0°。把曲柄2的初始位置设在与水平轴x2夹角为125°上,定义为曲柄2转角的起始点0°。
(2)曲柄1、2分别以各自的起始点0°为起始原点做相对转动,曲柄1作顺时针方向转动,其转角设为负值;曲柄2作逆时针方向转动,其转角设为正值。
(3)当曲柄1、2的相位角均处在各自的起始点0°时,图1中三角板的左侧边OG与连杆L6的GJ处在同一垂线OJ上,此时滑块位于上死点,见图2a。
(4)当曲柄 1、2 分别转动到-140°、+140°时,滑块处于下死点位置,如图2b所示。
(5)滑块处于上死点的位置定义为行程的零点,滑块向上运动为正,向下运动为负。
3.2 设定工艺参数
参照文献[6]及同等规格的瑞士GKP系列精冲压力机技术参数[7],设定九杆机构样机模型的工艺参数如表2所示。

表2 九杆机构样机模型工艺参数
3.3 滑块的标准行程、速度及扭矩曲线
在完成前面的建模及初始化参数设定之后,即可在MSC.ADAMS里面对样机模型进行仿真计算。
在不改变曲柄1、2初始相位差时(即曲柄1、2均处在各自的起始0°),同步驱动双曲柄,获得滑块在一个运动周期内的行程及速度曲线,称之为标准行程、标准速度曲线,如图3所示。

图3中,横坐标为两曲柄的转角,两曲柄转角相等方向相反。左边纵坐标为滑块行程,右边纵坐标为其对应的速度。
从图3可以看出,在一个工作周期内,滑块由下死点(非工作点)向上死点(工作点)快速上行,最大速度为165mm/s;在接近上死点10mm的范围内,滑块速度迅速降低,约45mm/s,即进入慢速工作行程;在到达上死点合模之后,停留一段将约70°的保压时间(占整个周期的19.4%),然后快速回程。
图4为空载状况下,曲柄1、2在一个工作周期内的扭矩曲线图。从图4可以看出,无论滑块上行还是下行,曲柄1的扭矩远远大于曲柄2的扭矩,且曲柄1在下死点附近的最大扭矩约为曲柄2的2倍。
4 曲柄初始相位差对滑块运动曲线的影响
两曲柄以同等转速同步驱动,转角相等方向相反(即曲柄1转速为-180°/s,曲柄2转速为+180°/s),改变曲柄1、2的初始相位差,研究其对滑块运动曲线的影响。
当曲柄1、2均处在各自的起始点0°时,如图2a所示,则定义两曲柄的初始相位差为0°。当曲柄2逆时针方向摆动形成一新初始相位,则称曲柄2初始相位超前。反之曲柄2顺时针方向摆动形成一新初始相位时,则称曲柄2初始相位滞后。本研究证明,曲柄2初始相位最大只能在超前60°和滞后60°的范围内调节。超前为正(+),滞后为负(-)。
4.1 曲柄2初始相位超前
选取曲柄2的三种相位差为研究对象:①无相位差,即 0°;②超前 30°;③超前 60°。可获得以下几组性能曲线。
4.1.1 滑块行程及速度曲线
从图5a中可以看出,曲柄2初始相位的超前可以使滑块行程变大,保压时间得到延长。当曲柄2初始相位超前60°时,滑块行程是0°状况下的两倍,保压时间延长到1.5倍。

从图5b中可以看出:①随着曲柄2初始相位的超前,滑块空载上行的速度越来越快。当曲柄2初始相位超前60°时,滑块空载上行的峰值速度是0°状况下的3倍;②在接近上死点约10mm的公称压力行程范围内,曲柄2初始相位的超前,使得滑块成形速度相对0°状况下的低且平缓,如图5b中点划线所示,这对提高制件质量非常有利;③滑块回程速度随着曲柄2初始相位的超前越来越快,当曲柄2初始相位超前60°时,滑块的最大回程速度是0°状况下的1.7倍。
4.1.2 空载状况下曲柄1、2的扭矩曲线
在图6a、b中,实线表示由上死点运行至下死点的下行阶段扭矩;虚线表示由下死点运行至上死点的上行阶段扭矩。
从图6a、b中可以看出,在空载状况下:①曲柄2初始相位的超前,会使曲柄1、2在整个周期内的扭矩分布呈增加趋势;②特别是在下死点附近,当曲柄2初始相位超前60°时,曲柄1的峰值扭矩相对无相位差(0°)状况下增加了3倍;曲柄2的峰值扭矩增加了5倍多。③而在上死点附近,曲柄1、2的扭矩增加不大。

4.1.3 全行程负载状况下曲柄1、2的扭矩分布
在滑块由下死点运行至上死点的全行程范围内加载1000kN的公称压力,获得其在整个上行阶段的曲柄1、2扭矩分布及载荷放大比曲线,见图7所示。其中载荷放大比定义为公称压力与浮动杆上所受载荷的比值,即:
载荷放大比=1000kN/F浮动杆

从图7中可以看出,在载荷的作用下:①在整体分布上,曲柄2初始相位的超前,会使曲柄1、2的扭矩急剧增加,且在下死点附近增加的幅度比上死点附近增加的大得多;②在局部分布上,接近上死点15mm的范围内,曲柄2初始相位的超前,对其自身扭矩影响不大,但对曲柄1的扭矩影响却很明显,见图7中的左上角。当曲柄2初始相位提前60°时,曲柄1在上死点15mm附近的扭矩是其在无相位差(0°)状况下的2.5倍;③曲柄2初始相位的提前,对载荷放大比曲线影响不大。在接近上死点60mm的行程范围内,放大比趋于一致,见图7右下角。
4.2 曲柄2初始相位滞后
与前者研究方法类似,选取曲柄2的三种相位差为研究对象:①无相位差,即0°;②滞后30°;③滞后60°。可获得以下几组性能曲线。
4.2.1 滑块行程及速度曲线
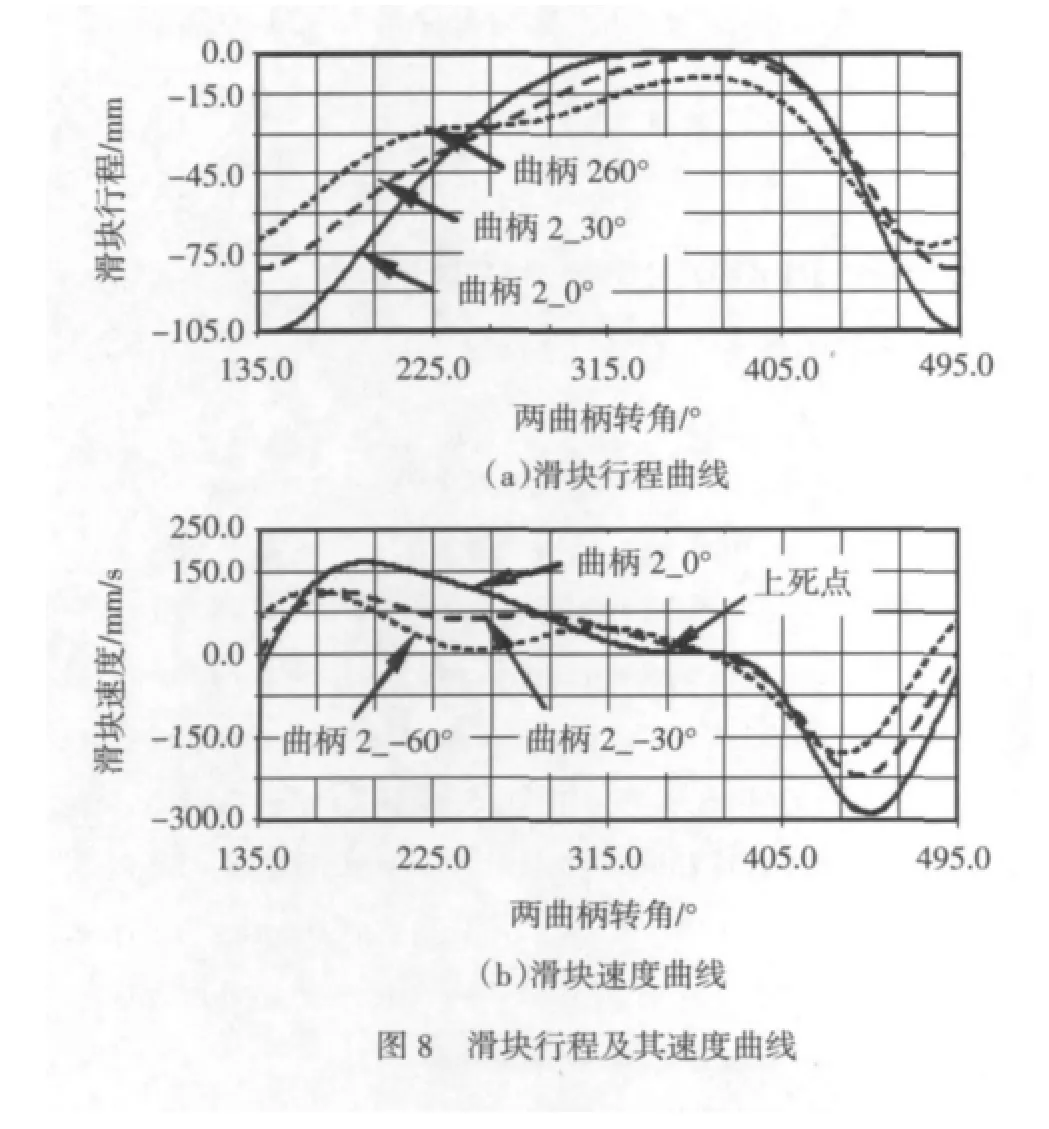
从图8a行程曲线中可看出:曲柄2初始相位滞后,使得滑块上死点降低,下死点升高,滑块行程变小。且滑块行程曲线会随着曲柄2初始相位的滞后而逐渐出现震荡双峰,当曲柄2初始相位滞后60°时,此时双峰最明显。
从图8b速度曲线中可以看出:曲柄2初始相位的滞后,使得滑块在非工作区域的速度降低,而在接近上死点附近的工作区域内,其成形速度却略有偏高。
4.2.2 空载状况下曲柄1、2的扭矩曲线
在图9a、b中,实线表示由上死点运行至下死点的下行阶段扭矩;虚线表示由下死点运行至上死点的上行阶段扭矩。
从图9中可看出:在空载状况下,曲柄2初始相位的滞后,对曲柄1在整个周期内的峰值扭矩影响不大,却能从很大程度上降低曲柄2的峰值扭矩。

4.2.3 全行程负载状况下曲柄1、2的扭矩分布
同4.1小节中的研究方法类似,也是在全行程范围内加载1000kN的公称压力,获得其在整个上行过程阶段的曲柄1、2扭矩分布及载荷放大比曲线,见图10。载荷放大比的定义与前文中的定义一致。
从图10中可以看出,在上行过程中,在载荷的作用下:①曲柄2初始相位的滞后,会使曲柄1、2的扭矩在整体分布上呈减小趋势,其扭矩分布与前者4.1图7中相位超前的相比,小一个数量级;②至于载荷放大比曲线,曲柄2初始相位的滞后,对接近上死点27mm范围内的载荷放大比影响不大,而对27mm范围之外的载荷放大比略有增大。
5 结论

本文主要对全伺服驱动的二自由度九杆机构进行了改变两曲柄初始相位差的同步控制研究,结论如下:
(1)在曲柄1、2同步转动的情况下,以两曲柄均处在各自的起始点0°为基准,曲柄2的初始相位,超前和滞后的角度只能介于±60°范围内变化。
若曲柄1的初始相位相对于自身起始点0°(即x1轴)摆动+φ或-φ,曲柄2的初始相位相对于自身起始点0°,同样也摆动-φ或+φ。此时曲柄2可超前和滞后的相位角同样为±60°。相应的性能曲线均不变。
(2)当曲柄2的初始相位超前时,随着曲柄2初始相位超前角度增大,滑块行程逐渐增大,保压时间相应延长。同时也会获得比较理想的速度曲线,即在接近上死点附近的工作区域内,滑块成形速度低而缓慢;而在非工作区域,滑块的上行与回程速度均很快。然而,在获得比较理想的行程曲线和速度曲线的同时,曲柄1、2的扭矩会随着曲柄2初始相位的超前而急剧增加。这样的工艺行程曲线适合于变形抗力较小且需要保压的薄板拉伸、折弯与压印等工艺。
(3)当曲柄2的初始相位滞后时,随着曲柄2初始相位滞后的角度增加,滑块行程减小,且会逐渐出现双峰震荡。滞后的初始相位,对空载状况下曲柄1、2的峰值扭矩影响不大,对负载状况下曲柄1、2的峰值扭矩却略有减小。然而,其速度曲线却不是很理想,即在接近上死点附近的工作区域内,滑块工作速度相对略有偏高,而在非工作区域,滑块空载上行与空载下行的速度反而偏低。这样的工艺行程曲线,适合于变形抗力较大的厚板冲裁、需要震荡拉延的成形工艺等。不过由于其在工作区域内的成形速度略有偏高,噪音可能会偏大,故在成形时可能需要进行降噪处理。
[1] 吕 言,周建国,阮 澍.最新伺服压力机的开发以及今后的动向[J].锻压装备与制造技术,2006,(1):11-14.
[2] 莫健华,郑加坤,古嗣伸裕,吕 言.伺服压力机的发展现状及其应用[J].锻压装备与制造技术,2007,(5):19-22.
[3] Yan Hongsen,Chen Weiren.A variable input speed approach for improving the output motion characteristics of Watt-type presses[J].International Journal of Machine Tools&Manufacture,2000,40(5):675-690.
[4] Yossifon S,Shivpuri R.Analysis and comparison of selected rotary linkage drive for mechanical presses[J].International Journal of Machinery Tools Manufacture,1993,(2):175-189.
[5] 何德誉.专用压力机[M].北京:机械工业出版社,1989:350-363.
[6] 李 辉,张 策,宋秩民.混合驱动精压机的优化设计和运动仿真[J].计算机辅助设计与图形学学报,2004,16(2):211-215.
[7] P.L.Tso,K.L.Liang.A nine-bar linkage for mechanical forming presses[J].International Journal of Machinery Tools Manufacture,2002,42:139-145.
Study of synchronization control in the 2-DOF planar nine-bar linkage system driven by servo-motor
HUANG Haibo,MO Jianhua,LV Yan,DU Erhu
(State Key Lab of Material Processing and Die&Mould Technology,Huazhong University of Science and Technology,Wuhan 430074,Hubei China)
A new servo-drive mode which uses servo-motor as the power input to drive the 2-DOF planar ninebar linkage system has been proposed in the text.The virtual prototype of such mechanism has been established and the simulation of synchronization control has been carried out by use of MSC.ADAMS software.Based on the results of this simulation,it can be concluded that several kinds of output motion curves could be easily achieved by only adjusting the initial phase position of the two cranks.In detail,when the initial phase position of crank 2 is ahead of crank 1,perfect output motion curves have been achieved despite of a minor increase in the two cranks'torque.Otherwise,the two cranks'torque has been reduced to a low level while the output motion curves are not so desirable.
2-DOF planar nine-bar linkage;Initial phase position difference;Servo press
TG385
A
1672-0121(2012)03-0030-05
2011-12-05
黄海波(1985-),男,硕士在读,主攻压力机的设计研究
