低水头电站导墙布置对进水口流态的影响

刘晓平，周千凯，周 俊，乾东岳

(长沙理工大学水利工程学院，长沙 410076)

1 问题的提出

水头损失对电站建成后机组的设计出力有较大影响，而低水头电站的问题则更加突出。因此，保证电站进水口水流流畅、进流匀称及流态平稳，并尽量减少水头损失是水利枢纽布置的主要内容。

布置枢纽建筑物时，电站及辅助建筑物和泄水闸之间一般会设置导墙。布置导墙的目的:一方面是把泄水区和引水区分开;另一方面是调顺电站上游的水流，使水流平顺均匀地进入发电机组。因此导墙的布置直接影响电站进水口流态。本文结合某水利枢纽电站的导墙布置，采用物理模型试验和数学模型相结合的方法，探讨了不同导墙布置形式对电站进水口流态及电站的影响。

该工程船闸和泄水闸布置于左岸，电站布置于右岸，电站导墙厚度为8 m，上、下游导墙长均为33 m，厂房宽度为110 m，共6台发电机组，单机引用流量为301 m3/s，电站进水口布置于厂房上游侧。电站布置见图1。

2 物理模型设计及结果分析

为了研究不同导墙布置对电站进水口流态的影响，试验结合某水利枢纽1∶100定床模型进行，采用VDMS表面流场测试系统，局部流速采用旋桨式微电脑流速仪，模型水位观测采用SCM60型水位测针。选择典型工况，即电站正常运行，其他泄水闸均关闭，导墙长度为b，电站横向宽度为l，定义b与l的比值为导墙的相对长度，以此作为导墙布置所考虑的因素，观察导墙附近的局部流态，以及观测不同方案下的电站上游水域的表面流场和水位变化规律，并分析其原因。

图1 电站布置图Fig.1 Layout of the power station

2.1 流态分析

选取典型工况，电站正常引用流量为1 806 m3/s，试验通过调整导墙的相对长度(b/l=0.25，0.4，0.6)的流场图见图2。

从图2可以看出，库区水流流速均匀且较平顺，当水流临近电站，水流逐渐转向至电站，受水流自身惯性作用，在导墙附近出现了漩涡。从漩涡形态上来看:在b/l=0.25导墙方案下的漩涡呈圆形，漩涡区最小，为28 m×5 m，流速在0.9～1.0m/s;b/l=0.4导墙方案下的漩涡趋于椭圆;b/l=0.6方案下的漩涡已变为长椭圆，漩涡区面积为72 m×15 m，漩涡流速范围在0.4～0.6m/s。在库区水深和流量恒定的情况下，水流在进入电站引水渠中受导墙的束窄而产生漩涡区，漩涡区面积与导墙的长度成正比。从漩涡区面积分析，布置导墙较短对流态有利，但考虑到导墙的布置还需满足其他工况中导墙对泄水闸泄流区与电站引水区的隔流作用，因此应选择合理的导墙长度。

根据图3，由于实际流体都有黏性，速度不等的流体层之间相互的剪应力可构成力矩而促使漩涡形成。漩涡形成后，由于漩涡远离导墙一侧流速较大，靠近导墙一侧水流受导墙阻碍流速减小，且流向相反，使漩涡的两侧存在压强差，在压强梯度的条件下，主流对漩涡产生侧推力W。漩涡在侧推力W和导墙边界的反作用力共同作用下平衡，而侧推力的大小直接会影响漩涡的形态。在W较小时，漩涡趋近于圆;当W较大时，漩涡会变形成椭圆。

以上对漩涡的理论分析解释了物理模型试验中的各方案下漩涡的不同形态。考虑到漩涡是能量的内部消耗，应尽量减少由漩涡造成的水头损失。对此，可以从电站的上、下游的位能大小来分析，下文将详述。

图2 电站上游导墙位置流态Fig.2 Flow patterns near the guide-wall in different schemes

图3 漩涡形成示意图Fig.3 Formation of vortex

2.2 电站上、下游水位分析

电站上、下游水位是衡量水流位能的重要参考依据，布置电站上、下游水位测点见图1，试验结果见表1。

表1 各方案水头试验结果Table 1 Results of water head tests

对进水口水位进行分析，按b/l=0.6布置导墙时的进水口水位最低，这是由于上游导墙过长使上游来流不能及时汇入至电站，导致在该方案下进水口水位较低。按b/l=0.25和b/l=0.4布置导墙时，进水口水位相差0.01 m，表明在上游水流汇入电站的入流能力接近。从电站下游水位分析，按b/l=0.6和b/l=0.4布置导墙时水位较低，表明水流从上游经过电站到下游后，水头损失较小，水流的出流能力较高。综合以上分析，按b/l=0.4布置导墙时，在上游能使水流较及时平顺地汇入电站，并经过电站出流水头损失较小。

3 数学模型建立与结果分析

为了进一步了解导墙布置对电站进水口流态的影响，需分析进水口的水流结构，但由于受物理模型试验观测手段的限制，无法完整地反应电站进水口前水域三维流场及其变化规律，因此采用数学模型和物理模型试验相结合的方法，进一步分析相应的水力特性及变化规律。

3.1 数学模型的建立

选择电站至上游的水域为计算区域，对边界进行适当简化，并建立概化模型，x轴方向为顺水流，模型采用雷诺平均数值模拟，用标准k-ε紊流模型。离散方法运用有限体积法对控制方程进行离散，对离散后的方程组采用显式求解方案，其中扩散项采用中心差分格式，对流项采用加权体积力格式。动量方程、紊动能及紊动能耗散率方程采用一阶迎风格式。

3.2 控制方程

连续方程:

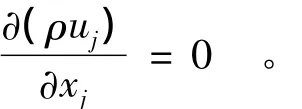
动量方程:

式中:ρ为流体密度;xi(i=1，2，3)为坐标轴;ui为时均速度;p*为包含紊动能的静压力，即p*=p+2ρk/3;μeff为有效黏性系数，等于分子黏性系数μ与Boussinesq涡团黏性系数μt之和，即μeff=μ+μt。

紊动能k和耗散率ε输运方程:

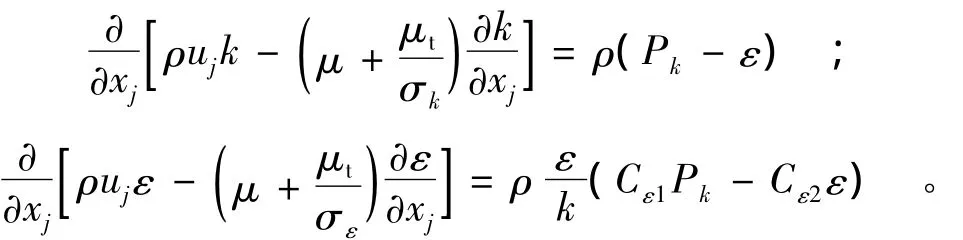
式中:μt为涡团黏性系数是紊动能生成项方程中各经验系数为

3.3 模型验证

为了验证数学模型的准确性，选取典型断面(模型入口断面和电站进水口前10 m的A－A断面，A－A断面位置如图1所示)的断面流速，与物理模型的观测值进行对比验证。

根据图4，物理模型实验观测断面流速散点分布于数模计算断面流速曲线附近，这表明断面流速分布均较吻合，数学模型计算的结果能够较好地反映导墙附近的流态。

3.4 流态分析

由5图可以看出，水流在进入电站时，受自身惯性，沿导墙产生了封闭的漩涡。对比图5(a)与图5(c)，按b/l=0.25布置导墙时，其漩涡流线贯穿了水深方向，这表明在流体内部有剧烈的相对运动，漩涡内部各层流线互相交织，表现出较强的三维特性;而按b/l=0.6布置导墙时，漩涡范围随导墙长度增加而增加，且漩涡流线各层分离，由于漩涡的封闭性，各层流线也仅在所在流体层重合，这表明由于导墙的延长使漩涡受到侧推力的作用而变为二维流态，此时流体内部的相对运动较弱。而按b/l=0.4布置导墙时，其流态介于三维与二维流态。

图4 典型断面流速分布数模与物模对比Fig.4 Comparison of typical section flow velocities in the mathematical model and the physical model

3.5 进水口前典型断面流速分布分析

考虑到漩涡会对进水口前流态产生影响，应从典型断面流速分布来分析在各方案下的计算结果，选择A－A和B－B断面(B－B断面位于电站进水口前30m)的流速分布进行分析，如图6。

典型断面 B－B位于进水口前30 m处，按b/l=0.25布置时，B－B断面为导墙临上游端，根据图6(a)可知:越靠近导墙的位置，流速越大，流速值在2.7m/s左右，表明水流受导墙的束窄，靠近导墙区域出现了流速极值;按b/l=0.4和b/l=0.6布置导墙，此时的B－B断面处于漩涡范围中，由于水流紊动的能量消耗，流速较小。断面流速曲线对x轴的积分为该断面的过流量，由图可知，按b/l=0.6布置导墙，其过流能力欠佳，不利于电站的引水。

由图6(b)可知:在远离导墙的的水流流态较平稳，越靠近导墙的水流流速分布呈递增趋势，而接近漩涡时，受导墙影响，流速梯度较大，在漩涡中心的流速最小，为0.11～0.22m/s，在导墙附近，流速有增大趋势。按b/l=0.25布置导墙时，流速极值出现在距导墙14.2 m位置;按 b/l=0.4布置导墙时，极值出现在距导墙20.8 m位置;按b/l=0.6布置导墙时，极值出现在距导墙39.7 m位置，流速极值的位置随导墙的加长向远离导墙位置移动，这表明漩涡的影响范围随导墙布置而变化。

根据以上分析，得出以下结论:①按b/l=0.6布置导墙时，其过流量最小，这是由于受导墙过长影响，上游水流不能及时汇入到电站，导致其过流能力最小;②按b/l=0.25布置导墙时，由于受束窄作用的水流距离进水口较近，断面流速分布曲线较陡，表明该方案下漩涡影响范围距进水口较近;按b/l=0.6布置导墙时，流速分布曲线较平缓，表明漩涡的影响范围已远离进水口;③综合对比分析，导墙的布置长度对进水口前断面流速存在临界点，即导墙存在一个特定长度，在此长度下对断面流速扰动较小，形成的漩涡产生的局部水头损失较小，过流能力最佳。在以上各导墙方案下，按b/l=0.4布置导墙时，满足以上要求，与物理模型结果一致。

图5 导墙附近三维流态Fig.5 Three dimensional flow patterns near the guide-wall in different schemes

图6 不同长度导墙下典型断面流速分布Fig.6 Velocity distributions in typical section with different guide-wall lengths

3.6 紊动能分析

鉴于出现在导墙附近的漩涡为紊流，根据紊动能的等值面图可以反映出进水口前水域的紊流范围及紊动强度，因此考虑从紊动能的角度分析其不同导墙下水流的变化规律。

图7 各方案紊动能等值面图Fig.7 Contour planes of turbulent kinetic energy in different schemes

从水流紊动范围上可以看出，考虑到水流紊动对电站进水口造成的影响，根据图7(a)，当按b/l=0.25布置导墙时，由于导墙长度较短，在电站进水口前水域紊动能在k=0.03 m2/s2的分布范围较小，产生的水头损失亦较小，因此有利于电站引水;但是由于该漩涡具有较强烈的三维流态，所以电站进水口的水流紊动较其他方案强烈，而紊动强烈的水流会对机组造成不利影响。根据图7(b)，当按b/l=0.6布置导墙，此时导墙长度最长，水流紊动区域的纵向范围较大，相应的水头损失较其他方案大，降低电站出力;但由于漩涡受导墙侧推力作用，减弱了水流的紊动作用，且在进水口的紊动范围与其他方案相比最小，利于机组运行。当按b/l=0.4布置导墙时，其紊动能k=0.03 m2/s2分布范围介于以上两者之间，表明其水头损失亦在上述两方案之中，而且流态已趋近于二维流态，对机组影响有限。根据上述分析，导墙的长度直接决定水流紊动范围，因此选择合理的长度不仅可以减少水头损失，还可以减少水流紊动，从而使水流平顺地进入电站。

导墙布置形式的不同对进水口前断面的紊动能分布影响亦较大。从图8可以看出，各方案下，紊动能的峰值均出现在距离导墙5～7 m的位置，直到50 m左右的位置，紊动能才趋于平缓，反映了导墙的紊动宽度在50 m左右。其中，当按b/l=0.25布置导墙时，导墙附近的漩涡紊动较其他方案强烈，紊动能的峰值在0.06 m2/s2;当按 b/l=0.4布置导墙时，其紊动能在0.05 m2/s2;当按 b/l=0.6布置导墙时，其紊动能峰值在0.04 m2/s2，这表明由于导墙的延长，使水流紊动强度发生变化。

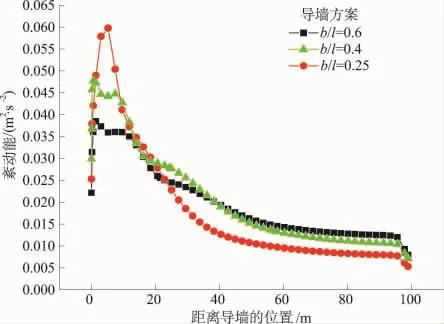
图8 A-A断面紊动能分布Fig.8 Distributions of turbulent kinetic energy in A-A section

综合考虑，只有选择合理的导墙长度，才能减少进水口前水流紊动范围和紊动强度，以达到利于电站发电的目的。

4 结论

基于以上分析，得出以下结论:

(1)在物理模型试验结果的基础上，通过理论分析，在平面二维形态上看，导墙的长度决定了作用于漩涡的侧推力W，随着导墙长度的增加，侧推力变大，漩涡由于四周受力不均，其形态会随着边界条件的变化而变化。

(2)根据数学模型计算结果，对于电站进水口前流态的影响，导墙存在一个特定长度，在此长度下对断面流速扰动较小，形成的漩涡产生的水头损失较小，且断面过流能力最佳。以上结论揭示了导墙附近流态的一些规律，对于合理选择导墙长度有一定指导意义，可以为其他类似工程所参考。

［1］陈云良，伍 超，叶 茂.水电站进水口水流流态的研究［J］.水动力学研究与进展(A 辑)，2005，(3):340－345.(CHEN Yun-liang，WU Chao，YE Mao.Research for Flow Pattern in Intake of Hydroelectric Station［J］.Journal of Hydrodynamics(Ser.A)，2005，(3):340－345.(in Chinese))

［2］林锦霖.水电站进水前池三维数值模拟［J］.广西水利水电，2009，(2):17－19.(LIN Jin-lin.3D Numerical Simulation for Receiving Basin of Hydropower Station［J］.Guangxi Water Resources＆ Hydro Power Engineering，2009，(2):17－19.(in Chinese))

［3］严忠民，蒋传丰，周春天.侧向进水前池水流特性的试验研究［J］.河海大学学报，1991，19(5):49－54.(YAN Zhong-min，JIANG Chuan-feng，ZHOU Chuntian.An Experimental Study on Flow Patterns in the Forebay with Side-intake［J］.Journal of Hohai University，1991，19(5):49－54.(in Chinese))

［4］杨正骏，林宗燊，谢佩珍.水工建筑物进水口自由表面漩涡试验研究［J］.水力发电学报，1987，(1):22－35.(YANG Zheng-jun，LIN Zong-xin，XIE Pei-zhen.Experimental Studies of Free-Surface Vortices at the Entrances of Hydraulic Structures［J］.Journal of Hydroelectric Engineering，1987，(1):22－35.(in Chinese))

［5］周济人，刘 超，汤方平.大型泵站前池水流流态的模拟［J］.水利水电技术，1996，(9):41－44.(ZHOU Jiren，LIU Chao，TANG Fang-ping.Simulation on the Flow Pattern in Diffusion Channel of Large Pump Station［J］.Water Resources and Hydropower Engineering，1996，(9):41－44.(in Chinese))

［6］彭有业.水电站进水口与尾水渠布置对机组出力的影响［J］.广西水利水电，2006，(3):50－65.(PENG You-ye.Influence of Intake and Tail Channel Layout of Hydropower Plant on Turbine Generator Output［J］.Guangxi Water Resources ＆ Hydro Power Engineering，2006，(3):50－65.(in Chinese))

［7］叶 茂，伍 超，杨朝晖.进水口前立轴旋涡的数值模拟及消涡措施分析［J］.四川大学学报(工程科学版)，2007，39(3):36－40.(YE Mao，WU Chao，YANG Zhao-hui.Numerical Simulation of Vertical Vortex at Intake and the Analysis of Anti-swirl Method［J］.Journal of Sichuan University(Engineering Science Edition)，2007，39(3):36－40.(in Chinese))

［8］邢英薇.不对称水流的数值模拟与试验研究［J］.人民珠江，2002，(5):10－12.(XING Ying-wei.Numerical Modeling and Experimental Research on Asymmetry Flow［J］.Pearl River，2002，(5):10－12.(in Chinese))

［9］严忠民.平原水闸泵站枢纽布置与整流措施研究［J］.河海大学学报，2000，(3):50－53.(YAN Zhong-min.Study on the Layout of Combined Sluice-Pump Station Projects and Modification of Flow Pattern［J］.Journal of Hohai University，2000，(3):50－53.(in Chinese))