高水头条件下氯离子击穿高岭土衬垫的离心模型试验研究

詹良通，曾 兴，李育超，钟孝乐，陈云敏

(浙江大学软弱土与环境土工教育部重点实验室，杭州 310058)

1 研究背景

压实黏土是我国填埋场中应用较多的一种防渗材料，广泛应用于填埋场衬垫以及封场覆盖。我国2007年颁布的《生活垃圾卫生填埋场防渗系统工程技术规范》(CJJ113－2007)［1］中推荐的4种衬垫形式中，压实黏土不仅作为一种重要的防渗材料与土工膜、GCL组合形成复合衬垫，而且本身就是一种单独的衬垫形式。我国《生活垃圾卫生填埋技术规范》(CJJ 17－2004)［2］中规定“天然黏土衬里或改性黏土衬里的渗透系数不应大于1.0×10－9m/s，且场底及四壁衬里厚度不应小于2m”。

衬垫作为填埋场的水平防渗防污结构，其性能的好坏直接关系到地下水污染控制效果。从目前的文献报道中发现我国部分填埋场底部的地下水及周边土壤污染超标。据中国环境监测总站2001年对各类345座垃圾处理场调查发现，345座垃圾填埋场中85%存在渗漏。北京阿苏卫填埋场一期工程底部设有黏土防渗层，1994年开始运行，2002年北京市市政管委会调查:阿苏卫填埋场地下水污染深度超过30 m。现场调查发现我国填埋场，特别是南方湿润气候区的填埋场的渗滤液水位普遍高达10多m，远高于规范规定的30cm;另外在现场施工中容易存在黏土衬垫的土料不符合要求、压实不够、施工不良等问题，衬垫渗透系数达不到规范要求的1.0×10－9m/s。

污染物在黏土衬垫中运移速度慢，设计击穿时间达数十年。普通的室内土柱试验，无法进行如此长历时的模拟。国外填埋场有关污染物运移的调查数据最长为20a［3］，国内调查数据最长为13a［4］，均小于衬垫的设计击穿时间。离心机具有缩时缩尺效应［5］，加速度为ng条件下，原型尺寸Lp对应模型尺寸Lm=Lp/n，原型时间tp对应模型时间tm=tp/n2，如100g重力加速度下，1d试验时间相当于原型27.4a。所以离心机模拟黏土衬垫中污染物运移具有很大优势。

Arulanandan等［6］研究了模拟污染物运移的相似问题，推导了污染物运移的8个相似比，说明了污染物离心模拟的条件，并用试验证明了污染物离心模拟的可行性。Hensley等［7］用离心机分别模拟了常浓度污染源和衰减浓度污染源两种情况下NaCl在粉土中的长期迁移特性，证明了离心模拟技术能为数学模型的验证提供有效的试验数据。Mckinley等［8］进行了无吸附性的污染物在饱和高岭土层中运移的离心模拟试验，污染源为浓度衰减的，试验后的浓度剖面与理论结果吻合较好。应用离心机模拟污染物运移，前人已经做了很多工作，但是以黏土衬垫为对象研究其防污性能的离心试验研究并不多。

本文针对目前填埋场中衬垫可能遭遇的现实工况，以黏土衬垫为对象，采用高岭土作为模型土样，应用离心机模拟氯离子在模型中的一维迁移，研究常浓度源下，高滤液水头条件和渗透系数对黏土衬垫的防污性能影响。

2 方案设计及实施方法

2.1 试验方案设计

本试验研究氯离子在2m厚黏土衬垫中的运移特性，探讨渗透系数和水头对污染物运移的影响。模拟污染物采用氯化钠，氯离子吸附性很小，一般可忽略其吸附性［6，8］。将纯净的NaCl颗粒和去离子水混合配置成0.1 mol/L的氯化钠水溶液模拟污染物溶液。

离心模型如图1所示，在制备好的衬垫模型上部加一定高度的NaCl溶液模拟衬垫上部水头。上机试验，经过一定的离心试验时间后，停机测试模型高度变化、顶部水头变化及底部收集水量，取样分析，检测氯离子在模型中的分布情况。

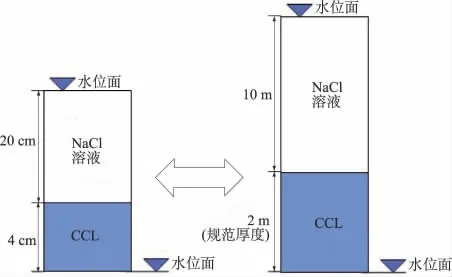
图1 模型示意图Fig.1 Schematic diagram of the model

试验所用衬垫模型的实际厚度为4.2cm，孔隙比e=2.617，水头高度为20cm，离心加速度为50g，离心时间为3h52min。

2.2 衬垫模型材料及制备

用于制作衬垫模型的土样为购买的商用高岭土粉末，为白色细颗粒粉末。基本土性试验结果表明本土样为高液限黏土，具体物理性质见表1。

表1 土样的物理性质指标Table 1 Physical parameters of soil sample

采用自制模型加压固结装置制备模型，得到压缩指数Cc=1.276(对应压力范围50～90 kPa)，回弹指数Ce=0.045。对不同固结压力下的土样取样做变水头渗透试验，得到白色高岭土和在不同孔隙比e对应的渗透系数。根据孔隙比e与渗透系数之间存在的经验关系拟合得:e=0.735ln(k)+13。该高岭土的固结系数为0.235mm2/s［9］。

考虑到黏性土的渗透性差，采用压实方法制作模型难以达到很高的饱和度。如在离心机内直接固结土样，则模型土样会出现从上到下逐渐密实的不均匀性。为了保证衬垫模型充分饱和且模型土样的均匀性，笔者先制备初始含水率很高的饱和泥浆，然后利用加压固结装置从泥浆状态开始逐级加压固结至目标模型。

先取定量的高岭土粉末与相应量的去离子水加入真空搅拌机内搅拌混合。在搅拌过程中同时抽真空，真空度为0.1MPa。将泥浆真空搅拌数小时，形成呈流态状的饱和泥浆后，再装入土样筒内，至设计高度。

衬垫模型的初始状态是高含水量的流态状泥浆，饱和度达99.9%。泥浆强度极低，无法直接加压，先令其在自然状态下排水，待有一定强度后再从低到高逐级加压固结。固结完成后衬垫模型的饱和度达100%，采用这种方式制备的衬垫模型为充分饱和。模型制备时施加的最大固结压力为50 kPa。

2.3 试验设备

试验中用于装模型土样的模型筒如图2所示。材料为有机玻璃，筒身为有机玻璃管，壁厚1cm，内径为9.8cm。模型筒底盖周围一圈内外安装有2个有一定高度的环，内侧为溢流环，外侧为积液环。溢流环顶部与置于模型筒底部的透水石顶面相平，通过小孔与筒底部相连通。模型筒高度为30cm。底部加滤纸、透水石后，净内高约为28cm。

图2 模型筒Fig.2 Modeling box

模型制备过程中使用自制反力架对模型进行加压固结。反力架上装有压力表盘，可以控制其施加的压力，在加压杆上装有百分表，量程为5cm，最小读数0.01mm，用来监测土样的固结沉降。

试验中使用的离心机为浙江大学ZJU-400g多用途离心机，最大能力400g-t，最大加速度为150g。开机至50 g和从50 g关机至停止，均耗时8 min。

图3 ZJU-400 g多功能离心机Fig.3 ZJU-400g multi-function centrifuge

2.4 离心模型试验方法

离心试验前，给模型筒中土样上部加上设计高度的NaCl溶液。用薄膜包裹模型筒上部，减少上部水头的蒸发量;用针在薄膜上钻一个小孔，防止形成真空。给下部溢流环加满去离子水，保持下部常水头。然后开机进行离心模型试验。离心机启动，离心加速度经过8 min时间从0 g增加到50 g，保持50 g稳定离心224 min，停机，经过8 min离心加速度从50 g变为0 g。试验中将停、开机的各8 min等效为8 min的稳定时间，故有效的离心时间为3 h 52 min。收集积液环中下部的渗透水量。测量上部水头高度、模型高度，称量模型质量、下部渗透水量。

将离心后的试验土样取出，沿厚度方向切成11片，记录各片土样质量，再烘干，称量土样质量，计算土样含水率。将烘干的土样研磨成粉末，称取1 g粉末加50 mL去离子水混合，振荡24min，离心后取1mL上清液，用去离子水稀释至100mL。再采用离子色谱仪分析稀释溶液中的氯离子浓度，从而反算出切片土样内的氯离子浓度，获得模型中的氯离子浓度剖面。

3 离心试验结果及分析

3.1 离心试验过程中模型固结沉降及渗漏量

由于离心模型在高渗透压力作用下发生固结，固结排水量对模型中污染物运移过程及渗漏量有影响，所以必须首先分析离心试验过程中模型固结沉降。

离心试验前模型高度4.2cm，孔隙比e为2.617，初始含水量99.53%，水头高度20cm。经过3.87 h的离心时间，测量结果表明上部溶液水头下降1.28cm，折合成入流水量为96.6 mL，而下部溶液收集装置积液环收集到的水量为55.1 mL。切片分析时，测量得模型土样的质量、高度和含水率，如表2所示。

表2 模型土样切片测试得到模型参数Table 2 Parameters of the sliced soil sample

切片时测试模型土样的含水量分布，如图4所示，从顶部到底部含水量逐渐变小，顶部含水量为97.5%，底部含水量为85.3%，平均含水量为93.37%。这反映了离心过程中随深度增加，土样有效应力增大，导致了含水率随深度增加而降低。

图4 含水量随深度分布图Fig.4 Moisture profile of the model

由于土样在试验前后含水率变化，根据图5可得离心试验中由于固结排出的水量Δmw=14.19 g，推算出模型应沉降0.188cm，即模型排水后高度应为4.012cm，与实测值接近。

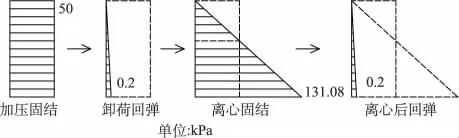
图5 各阶段模型内部应力分布Fig.5 Stress distribution in the model in different stages

模型从泥浆状态加压固结到上机离心再到离心结束这个过程中，应力状态变化经历4个阶段，如图5所示，图中虚线代表先期固结压力，实线代表各阶段实际应力。模型制备阶段，模型内部受均布应力，大小为固结压力50 kPa。固结完成后卸载，此时模型所受的应力仅为1 g状态下的自重有效应力0.2 kPa，模型发生回弹。上机试验时，离心加速，渗透力和土自重均被放大为原来的50倍，模型应力为三角形分布，底部最大应力为131.08 kPa，模型将发生固结。离心结束后，所受应力又变为1 g状态下的自重有效应力0.2 kPa，土样将发生回弹。

离心试验阶段，模型固结沉降分成2部分考虑，模型上部1.6cm部分应力小于模型土样的先期最大固结压力50 kPa，故该部分土样发生再压缩，这部分压缩量计算采用回弹指数，计算压缩量为0.056cm;1.6cm以下的模型土样应力大于50 kPa，这部分的土样由超固结状态转变为正常固结状态，其压缩量分两段计算:第1段采用回弹指数，计算压缩量为0.082cm，第2阶段采用压缩指数，计算压缩量为0.236cm。离心固结阶段，共计算沉降了0.374cm，离心固结后土样高为3.826cm。离心结束后模型回弹，回弹量计算采用回弹指数，计算回弹量为0.146cm，离心结束后的模型高度为3.972cm。计算得到的离心前后总沉降为0.228cm。

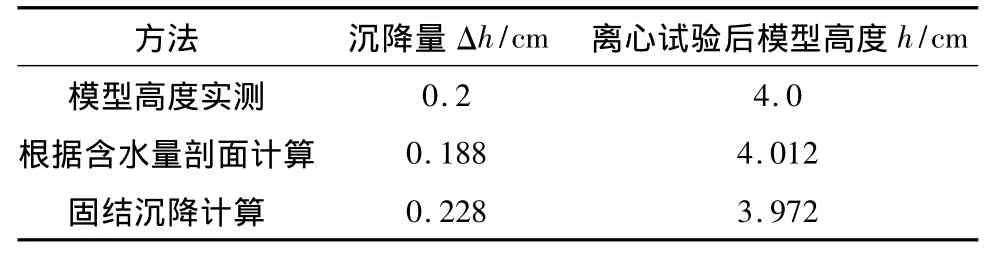
表3 不同方法获得的离心试验前后沉降比较Table 3 Comparison of model settlements before and after the test obtained by different methods

以上分析说明离心过程模型发生了固结，实测沉降与根据含水量剖面计算较为接近，固结沉降计算的存在一定误差，可能与参数选取有关。

开机阶段离心机经历加速过程，在停机阶段处于减速过程，在分析土中应力时，忽略开机阶段的离心加速度变化。图6为离心固结完成时的土中应力分布。离心固结初始阶段，孔隙水压力与总应力相等，土中有效应力为0.2 kPa，超孔压为正三角形分布，大小为固结完成时的有效应力减去当前有效应力，底部最大值为130.88 kPa。

图6 离心状态下孔压和有效应力分布Fig.6 Pore pressure and effective stress distribution of soil sample in centrifugal state

根据双面排水、初始孔压为正三角形分布的一维固结解析解，可以得到离心固结阶段不同时间的超孔压消散。图7给出了各时刻的超孔压剖面分布，P0为初始超孔压，即130.88 kPa，时间单位为min。

如图7所示，固结初期最大超孔压出现在模型下部，随着时间增加孔压逐渐消散。平均固结度达到90%的时间 t90=27.4 min。

图7 不同时间沿深度的超孔压分布Fig.7 Pore pressure profiles at different times

为了得到模型在离心过程中的通过上下边界渗流的水量，将固结产生的超孔压和上部水头产生静水孔压叠加，得到沿深度的水头分布，进一步得到不同时间沿深度水力坡降，如图8所示。

图8 不同时间沿模型深度的水力坡降分布Fig.8 Hydraulic gradient profiles at different times

图8中水力坡降i＜0的点，发生向上渗流;水力坡降i＞0的点，发生向下渗流。如图8所示，t＜6.8 min时，模型上部水力坡降 i＜0，表明存在向上的渗流，随着时间增加，发生向上渗流的区域越来越小。t≥6.8 min时，沿深度各点的水力坡降均≥0，模型中渗流一致向下。

在模型固结过程中，顶部边界的水力坡降从负的(向上)变为0，再增大至稳定水力坡降，这个过程中流速是变化的，甚至还存在向上渗流的情况。为了考虑不稳定的渗流对污染物运移的影响，这里引入“等效时间”的概念，即将不稳定的渗流时间根据流量相等的原则等效为稳定渗流的时间。如图9所示，t=21 min左边入流量曲线与时间轴之间的面积，等于右边入流量曲线与稳定入流量线之间的面积。所以等效的运移时间为232－21=211 min，即3.517 h。

图9 上边界入渗率随时间的变化Fig.9 Rate of inflow through the upper boundary vs.time

应用达西定理，根据渗透系数和边界处不同时刻的水力梯度，即可求出各时刻的模型底面的渗漏率。计算采用根据上部入渗水量拟合得到的渗透系数3.2×10－9m/s。图10中给出了离心试验过程中模型底部的由固结引起的渗漏率、总的渗漏率随时间的变化。固结引起的渗漏量在初始阶段很大，随着时间增加逐渐变小，这反映了孔压消散过程。总渗漏量中另一部分为模型上下水头差引起的渗流量，当固结结束后，渗漏量为稳定值，大小为30.2 m/a，转化为原型渗漏量为0.604 m/a。谢海建［10］计算的渗透系数为1.0×10－9m/s的2 m压实黏土衬垫在10 m上覆水头下，渗漏率为0.189 m/a，考虑到本文衬垫渗透系数为3.2×10－9m/s，两者结果吻合。

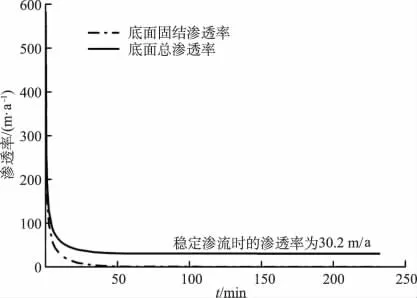
图10 底部渗漏率随时间的变化Fig.10 Rate of outflow through the bottom vs.time

3.2 孔隙水中氯离子浓度分布实测结果及理论反分析

离心后切片分析模型孔隙水中氯离子浓度随深度的分布，实测结果如图11所示，离散点为实测的浓度值。

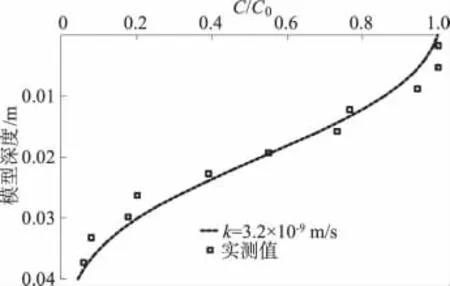
图11 氯离子的拟合浓度曲线Fig.11 Fitted chloridion concentration curve

对于污染物在饱和多孔介质的一维竖向运移问题，用对流-弥散方程描述拟合

边界条件:

方程的解［11］为

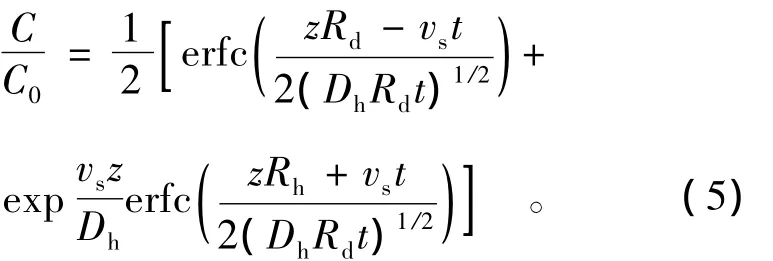
顶部边界条件(3)，表示上部为指定常浓度，下边边界条件(4)表示为半无限空间体，可近似用于有限厚度土层的分析［12－15］。根据上面的解，可得衬垫模型的拟合浓度曲线(图11)，连续曲线为理论拟合值。

由于上覆水头的变化很小，拟合中取平均水头按常水头考虑。由于试验中采用低吸附性的NaCl作为目标污染物，且试验历时较短，理论分析中不考虑阻滞作用［8］，取Rd=1.0;Dh为水动力弥散系数，为有效分子扩散系数，根据经为弥散度，为拟合参数，vs为渗透速度，根据模型渗透系数和水力梯度计算得到，渗透系数取根据上边界水量分析为3.2×10－9m/s。离心加速度50 g，离心试验时间按等效后的3.517 h考虑，对应的原型时间366 d。具体计算参数如表4所示。

表4 衬垫模型的拟合运移参数Table 4 Fitted movement parameters for liner model

4 高岭土衬垫击穿时间预测

根据上面试验拟合得到的运移参数Dd和α，对上部水头10 m，渗透系数为3.2×10－9m/s的2 m厚黏土衬垫对击穿时间进行预测，结果如图12所示。1.53 a时，衬垫底部出流浓度达1%初始浓度;1.97 a底部出流为初始浓度的10%。如取击穿浓度为初始浓度的10%时，仅需1.97 a衬垫即被击穿。若衬垫渗透系数降低为规范规定的1.0×10－9m/s，上覆 10 m 水头时，击穿需要2 052.6 d，即5.62 a。所以在高渗滤液水头作用下填埋场底部渗滤液极易击穿衬垫，污染地下水。

图12 氯离子的击穿时间模拟Fig.12 Predicted times of chloridion breaking through the liner model

本试验是以氯离子为目标污染物，由于Cl－吸附性很小，对于重金属等强吸附性离子，实际击穿时间应更长［18－19］。根据污染物在黏土中常见的阻滞因子Rd的取值，下面模拟了10 m水头下，3种吸附性不同的污染物在不同渗透系数的衬垫中运移的击穿时间。

对于高吸附性的污染物，击穿时间随着吸附性增加而变长。因此对于重金属等在黏土中有很强的吸附性的污染物，在预测衬垫击穿时间时应考虑衬垫材料对相应污染物的吸附性。

图13 不同吸附性离子击穿衬垫的时间比较Fig.13 Comparison of Chloridion breakthrough timewith different retardation factors

5 结论

用离心机模拟高水头条件下污染物的运移时，离心加速导致模型产生高的渗透压力，如果产生的渗透压力大于模型的先期固结压力时，模型会在离心机内发生固结。固结时模型中渗流方向及速度随深度和时间变化，导致理论模拟分析困难。由于黏土中超孔压消散慢，固结时间长，对污染物运移影响大，因此在进行类似试验时，应该设法消除模型固结排水对污染物运移的影响。

本文通过等效时间的方法，对离心试验结果进行拟合，根据拟合的参数对原型的击穿时间进行预测，预测结果表明在10 m水头作用下渗透系数3.2×10－9m/s的2 m厚黏土衬垫被氯离子击穿时间为1.97a，渗漏量为0.604 m/a，当渗透系数降低为规范规定的1.0×10－9m/s时，击穿时间为5.62 a。预测结果也表明污染物的阻滞因子Rd越大，击穿时间越长。采用离心机模拟污染物在低渗透性模型中的运移时，由于污染物运移速度显著增加，试验历时缩短，吸附作用没能充分发挥，可能导致预测的击穿时间偏大。

［1］CJJ113－2007，生活垃圾卫生填埋场防渗系统工程技术规范［S］.北京:中国建筑工业出版社，2007.(CJJ113－2007，Technical Code for Liner System of Municipal Solid Waste Landfill［S］.Beijing:China Architecture ＆ Building Press，2007.(in Chinese))

［2］CJJ 17－2004，生活垃圾卫生填埋技术规范［S］.北京:中国建筑工业出版社，2004.(CJJ 17－2004，Technical Code for Municipal Solid Waste Sanitary Landfill［S］.Beijing:China Architecture ＆ Building Press，2004.(in Chinese))

［3］ROWE R K.Long-Term Performance of Contaminant Barrier Systems［J］.Geotechnique，2005，55(9):631－678.

［4］谢 焰，谢海建，陈云敏，等.填埋场底土污染物浓度实测值和理论解的比较［J］.自然灾害学报，2009，18(5):62－69.(XIE Yan，XIE Hai-jian，CHEN Yunmin，et al.Comparisons of Measurements of Contaminant Concentration in Landfill Bottom Soils with Theoretical Solutions［J］.Journal of Natural Disasters，2009，18(5):62－69.(in Chinese))

［5］TAYLOR R N.Geotechnical Centrifuge Technology［M］.London:Blackie Academic and Professional，1995:296.

［6］ARYLANANDAN K，THOMPSON P Y，KUTTER B L，et al.Centrifuge Modeling of Transport Processes for Pollutants in Soils［J］.Journal of Geotechnical Engineering，ASCE，1988，114(2):185－205.

［7］HENSLEY P J，SCHOFIELD A N.Accelerated Physical Modelling of Hazardous-Waste Transport［J］.Geotechnique，1991，41(3):447－465.

［8］MCKINLEY JD，PRICE A，LYNCH R J，et al.Centrifuge Modelling of the Transport of a Pulse of Two Contaminants［J］.Geotechnique，1998，48(3):421－425.

［9］ELMES D R.Creep and Viscosity in Two Kaolin Clays［D］.UK:University of Cambridge，1985.

［10］谢海建，詹良通，陈云敏，等.我国四类衬垫系统防污性能的比较分析［J］.土木工程学报，2011，44(7):133－140.(XIE Hai-jian，ZHAN Liang-tong，CHEN Yunmin，et al.Comparison of the Performance of Four Types of Liner Systems in China［J］.China Civil Engineering Journal，2011，44(7):133－140.(in Chinese))

［11］OGATA A，BANKS R B.A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media［G］.Professional Paper(Geological Survey(U.S.No.411－A.Washington:U.S.Government Printing Office，1961.

［12］SHACKELFORD C D.Transit-Time Design of Earthen Barriers［J］.Engineering Geology，1990，29(1):79－94.

［13］NAKAJIMA H，HIROOKA A，TAKEMUR A J，et al.Centrifuge Modeling of One-Dimensional Subsurface Contamination［J］.Journal of the American Water Resources Association，1998，34(6):1415－1425.

［14］CELORIE J，VINSON T，WOODS S，et al.Modeling Solute Transport by Centrifugation［J］.Journal of Environmental Engineering，1989，115(3):513－526.

［15］VAN GENUCHTEN M TH，PARKER J C.Boundary Conditions for Displacement Experiments through Short Laboratory Soil Columns［J］.Soil Science Society of A-merica Journal，1984，48(4):703－708.

［16］SHARMA H D，REDDY K R.Geoenvironmental Engineering:Site Remediation，Waste Containment，and E-merging Waste Management Technologies［M］.New Jersy:John Wiley ＆ Sons，Inc.，2004.

［17］谢海建.成层介质污染物运移机理及衬垫系统防污性能研究［D］.杭州:浙江大学，2008.(XIE Hai-jian.A Study on Contaminant Transport in Layered Media and the Performance of Landfill Liner Systems［D］.Hangzhou:Zhejiang University，2008.(in Chinese))

［18］LO I M C，ZHANG Jian-hong，HU Li-ming.Centrifuge Modeling of Cadmium Migration in Saturated and Unsaturated Soils［J］.Soil and Sediment Contamination.AHA，2005，14(5):417－431.

［19］SHACKELFORD C D.Critical Concepts for Column Testing［J］.Journal of Geotechnical Engineering，1994，120(10):1804－1828.