折线河岸边坡稳定性的研究

王曙光，李 亮，赵炼恒，刘 浩，3

(1.贵州省交通规划勘察设计研究院股份有限公司，贵阳 550001;2.中南大学 土木工程学院，长沙 410075;3.中铁工程设计咨询集团有限公司，北京 100055

1 研究背景

河岸边坡失稳是一个很复杂的课题，河流来水、来沙条件、河岸土壤条件、河岸边坡坡顶荷载、坡体内部水压力等是影响河岸边坡失稳的重要因素。在汛期，由于河流水流很急，其携带泥沙能力增强，河床易产生冲刷下切或岸滩发生侧向侵蚀而淘刷，形成陡立岸滩，甚至形成倒坡岸滩，此时，河岸边坡易发生失稳。河岸边坡土压力计算类似于挡土墙土压力计算，在坡顶荷载和河床冲刷下切等因素共同作用下，河岸边坡内部土压力达到主动极限平衡状态，坡顶出现张拉应力，致使坡顶出现张拉裂缝［1］。同时，临河边坡水位升降也是影响河岸边坡稳定性的一个重要因素［1－4］。

目前，河岸边坡稳定性分析是很多学者的研究重点。大部分研究主要从崩塌临界高度、水位升降、流水淘刷、破坏机理等方面进行，文献［1］研究了折线边坡的临界崩塌高度，文献［2－10］就水位升降和流水淘蚀对边坡稳定性影响进行了研究，文献［11－13］分析了河岸崩塌机理，等等。文献［1］提出了折线边坡的计算模型，文献［3］研究了在多因素作用下单一岩质边坡的稳定性分析。但在以往的研究当中，尚未综合考虑到折线土质边坡在多因素作用下其抗滑稳定系数的变化。针对该问题，本文基于折线土质边坡，采用极限平衡法，综合考虑了坡顶行车荷载、静水压力、流水淘蚀、地震等荷载因素的影响，推导了折线河岸边坡在多因素影响下的抗滑稳定系数，并重点分析了裂隙水位、河流水位、坡趾淘刷等因素对折线河岸边坡稳定性的影响。

2 边坡计算假设及计算模型

图1 原状河岸边坡计算模型Fig.1 Calculation model of the original river bank slope

参照文献［1］与文献［3］的研究成果，假定典型的河岸边坡横剖面如图1所示，为了便于计算，作如下假定:①滑动面或破坏面为一平面，且滑体为同一土层;②滑动面在破坏时滑动面上的应力处于极限平衡状态;③由于车辆荷载等影响下有张拉裂缝出现在坡顶，张裂缝直立;④不考虑水的浸泡对于土的黏聚力c和内摩擦角φ的影响。

几何要素有:坡高H、临河水位的高度Hr、第一阶边坡坡高H1、第一阶边坡坡角θ1、第二阶边坡坡角θ、边坡失稳倾角θ3、张裂缝深度H3、张裂缝积水深度Z和张裂缝距坡顶缘的水平距离b。当考虑边坡坡趾被淘刷时，此时河岸边坡横剖面如图2所示，DMN区域为水流淘蚀部分，淘刷高度为H－H2，淘刷切入角度为π－θ0。

图2 流水淘刷作用下的河岸边坡计算模型Fig.2 Calculation model of river bank slope subjected to stream erosion

作用的荷载有:由于一侧为临河，需要考虑作用在临空面上的静水压力，采用静水压力法计算边坡中的水压力［14－15］，见图中 R1至 R5;当考虑河岸边坡上部行车效应时，假设坡顶均布载荷q;当考虑偶然荷载如地震效应或爆破震动时，采用拟静力的方法考虑动荷载效应［3，16，17］。

3 河岸边坡受力及稳定性分析

3.1 原状边坡稳定性分析

当河岸边坡坡趾未被冲刷时，考虑上述因素的影响，河岸边坡受力状态如图1所示。

对于原状边坡，当河岸坡脚未淘刷时，根据几何条件，此时崩塌体的有效重量为

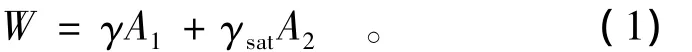
式中:A1为渗透面以上的滑体面积;A2为渗透面以下的滑体面积;γ为土体的天然重度;γsat为土体的饱和重度。

假设整个滑体面积为A，则

(1)当临河水位高于第二阶边坡，且高于裂隙水位，即Hr≥(H－H1)时，且 Hr≥(H－H3+Z)时，面积A1计算采用以下公式:

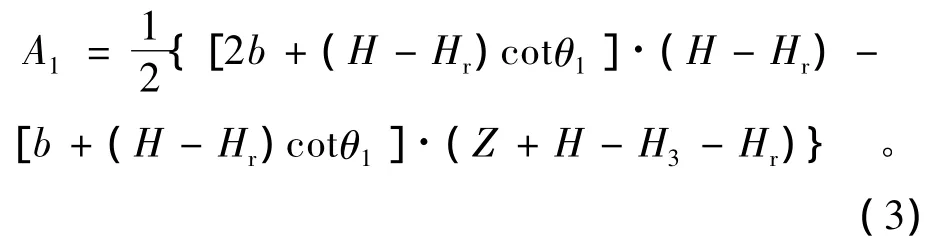
(2)当临河水位高于第二阶边坡，但低于裂隙水位，即(H－H1)≤Hr≤(H－H3+Z)时，面积 A1计算采用以下公式:

(3)当临河水位低于第二阶边坡，即0≤Hr≤(H－H1)时，面积A2计算采用以下公式:

又A1+A2=A，可以分别求出A1与 A2。

对于地震荷载，目前常采用拟静力分析法(quasi-static analysis)［3，16，17］。假设滑坡为刚体，地震作用力分解为水平和竖直2个方向的等效力，此时水平和竖向地震效应荷载为khWrock和kvWrock。且二者作用于刚体质心处，假设kh和kv关系有如下关系:

式中:ζ为kv相对于kh的比例系数;ζ取正值表示作用力方向向下;ζ取负值表示作用力方向向上。其中kh一般取值为0.0～0.3，而ζ一般取值为－1.0～1.0［3、16、17］。

静水压力R1～R4计算采用静水压力法计算。

岸坡静水压力R1和R2:

(1)当临河水位高于第二阶边坡，即Hr≥(HH1)时，静水压力计算采用以下公式:

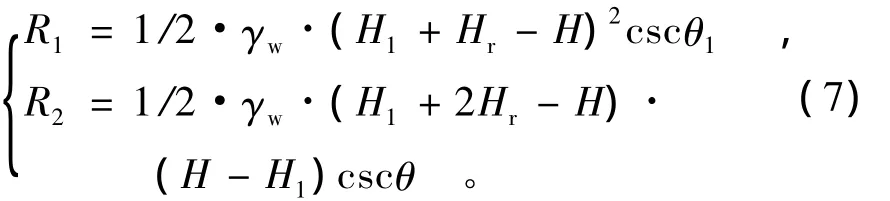
(2)当临河水位低于第二阶边坡，即Hr＜(HH1)时，静水压力计算采用以下公式:

张裂隙水压力R3为

滑面CD上作用的静水压力R4为

由图1所示的几何关系，可得CD长度l为

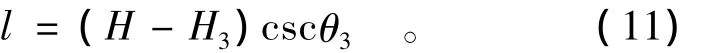
应用极限平衡法，由抗滑稳定系数定义可知:

因此，在复杂受力条件下，求得原状河岸边坡的稳定系数K:

式中:c为岸坡土体的黏聚力;φ为土体的内摩擦角;R1为岸坡AE上作用的静水压力;R2为岸坡DE上作用的静水压力;R3为BC上作用张裂隙水压力;R4为CD上作用的静水压力;W为滑体的有效重量;kh和kv分别为地震荷载在水平和竖直2个方向的等效力系数;q为作用在岸坡上部的均布荷载;β为渗透力与水平方向的夹角;l为滑面CD的长度。

根据临河水位与裂隙水位、边坡高度之间的关系将以上各条件下的(1)至(12)式代入式(13)，即可以求出相应条件下原状边坡的稳定系数。

3.2 坡趾淘蚀边坡稳定性分析

假设坡趾ΔDMN被淘刷，河岸的受力分析如图(2)所示。

参照文献［1］，此时滑体面积A为

(1)当临河水位高于第二阶边坡，且高于裂隙水位，即Hr＞(H－H1)时，且 Hr＞(H－H3+Z)时，面积计算采用以下公式:

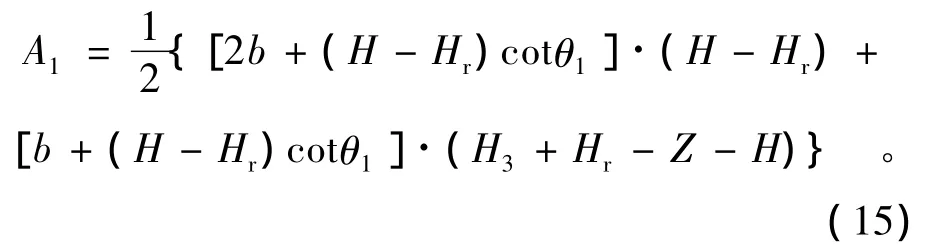
(2)当临河水位高于第二阶边坡，但低于裂隙水位，即(H－H1)≤Hr≤(H－H3+Z)时，面积计算采用以下公式:

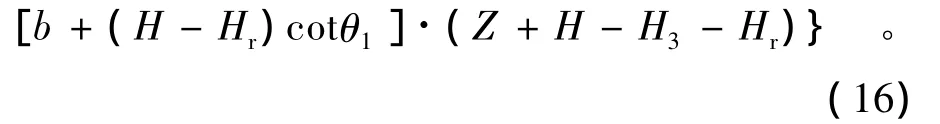
(3)当临河水位低于第二阶边坡，但高于淘刷高度，即(H－H2)≤Hr≤(H－H1)时，面积计算采用以下公式:

(4)当临河水位低于淘刷高度，即0≤Hr≤(H－H2)时，面积计算采用以下公式:

由式(14)～(18)可以求得对于不同临河水位高度条件下的面积A1和A2。

静水压力R1，R2，R5的计算如下:

(1)当临河水位高于第二阶边坡，即Hr＞(HH1)时，静水压力计算采用以下公式:

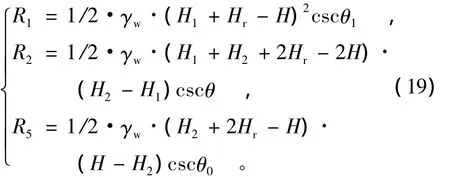
(2)当临河水位低于第一阶边坡，但高于淘刷高度，即(H－H2)≤Hr≤(H－H1)时，静水压力计算采用以下公式:

(3)当临河水位低于淘刷高度，即0≤Hr≤(H－H2)时，静水压力计算采用以下公式:

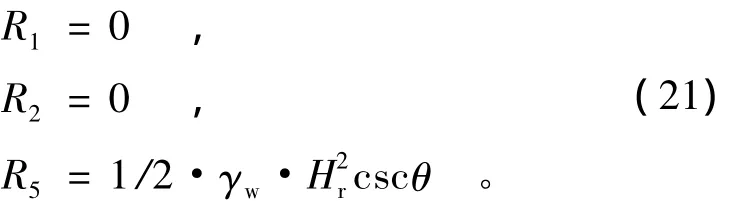
静水压力R3的计算仍采用式(9)。

R4的计算采用式(10)。

滑面l的计算同式(11)。

当坡址被淘刷时，在多因素作用下，边坡稳定系数如下:

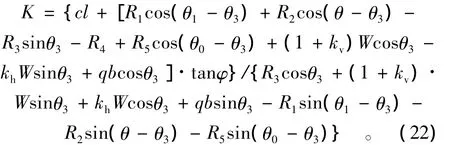
式中:R5为MN上作用的静水压力，其余各参数含义不变。

将相应条件下的各式代入式(22)式，即可以求出复杂条件下坡趾淘刷边坡的稳定系数。

4 河岸边坡稳定性算例分析

影响河岸边坡的失稳的因素相当复杂，本文重点研究了临河水位升降、裂隙积水深度、静水压力等对于临河边坡的稳定性影响，下面将设置一些特殊的参数分析河岸边坡稳定性。

4.1 张裂缝产生与水位升降对原状河岸边坡稳定性的影响

4.1.1 张裂缝产生对原状河岸边坡稳定性的影响

在河岸边坡坡顶行车与流水冲刷等因素影响下，此时河岸边坡内部土压力计算类似于挡土墙土压力计算，河岸边坡内部达到主动极限平衡状态，坡顶出现张拉应力，致使坡顶出现张拉裂缝，张拉裂缝的形成是导致河岸边坡失稳的重要因素。

当河岸坡趾尚未被淘刷时，其计算简图见图1，并假设几何参数为:H=7 m;H1=3 m;b=4 m;θ=45°;θ1=60°;θ3=27.2°;γ=18kN/m3;γw=10kN/m3;c=25 kPa;φ=25°;q=100kN/m;kh=0.2;ζ=0.5;H3=2 m。取临坡河流水位 Hr分别为2，4，5，6 m。当张裂缝深度Z=0～2 m变化时，此时河岸边坡抗滑稳定性安全系数变化如图3所示。

由图3可知:张裂缝的产生对于河岸边坡稳定性影响较大。随着张裂缝积水的增加，边坡稳定性系数逐渐减低，边坡愈趋于不稳定，另一方面，较高水位对于维持边坡稳定性有利。

4.1.2 水位升降对原状河岸边坡稳定性的影响

为了更加清楚地说明水位升降对于河岸边坡稳定性的影响，假设条件见4.1.1。取张裂缝积水深度Z分别为0，1，2 m，当临坡河流水位 Hr=0～7 m(Hr/H=0～1.0)之间变化，此时河岸边坡抗滑稳定性安全系数变化如图4所示。

由图3、图4可知:水位升降与裂隙积水对原状边坡稳定性有着重要影响。在边坡几何参数不变的情况下，临河水位固定在同一高度Hr，边坡稳定系数随着裂隙水位的升高而降低;另一方面，当裂隙水位固定在同一高度Z，随着临河水位的升高，边坡稳定系数先变小再增大。因此，在工程实际中，应密切关注临河水位的升降，同时做好坡体内部的防排水措施。

图3 张裂隙积水对原状边坡稳定性的影响Fig.3 Effect of water-filled tension crack on the stability of original slope

4.2 河床淘蚀作用对河岸稳定性的影响

由于河岸坡趾长期受水流浸泡，以及流水所携带泥沙对于河流坡趾的冲刷，河床易冲刷下切，形成倒立岸坡，甚至形成倒坡岸坡，这对河岸边坡稳定性相当不利，以下将详细分析河岸坡趾淘刷对于河岸稳定性的影响。

4.2.1 水位升降与淘刷深度的影响

假设坡趾淘刷高度不变，即H2=6.75 m，由于来水来砂等因素影响，坡趾淘刷切入深度逐渐增加。

取H=7 m;H1=3 m;H3=2 m;b=4 m;θ=45°;θ1=60°;γ=18kN/m3;γw=10kN/m3;c=25 kPa;φ=25°;q=100kN/m;kh=0.2;ζ=0.5。张裂缝积水深度Z=1 m，淘刷切入角度θ0分别取90°，120°，135°，150°，当临坡河流水位 Hr=0～7 m(Hr/H=0～1.0)变化时，此时河岸边坡抗滑稳定性安全系数变化如图5所示。

图5 水位升降与淘刷切入深度对边坡抗滑稳定性的影响Fig.5 Effect of water level fluctuation and cutting depth of stream erosion on the slope stability

由图5可知:水位升降与河床淘刷深度对边坡稳定性影响很大。当坡趾淘刷高度不变时，坡址因流水淘刷由陡立变成倒立时，边坡稳定系数变小，边坡愈趋于不稳定;同时，随着水位的升涨，边坡稳定系数先逐渐变小后慢慢增大。这说明，河床的淘刷对于边坡的稳定性非常不利，因而在工程实际中，应加强临河边坡坡趾的抗冲刷能力，同时需密切关注河流水位的升降。

4.2.2 水位升降与淘刷高度的影响

为了更好地说明河床淘刷对边坡稳定性的影响，假设坡趾淘刷角度保持不变(θ0=135°)，而淘刷高度逐渐增加(H－H2=0～1 m)，其它条件取值见4.2.1。张裂缝积水深度Z=1 m，淘刷高度h=HH2=0～1 m，当临坡河流水位Hr=0～7 m(Hr/H=0～1.0)变化时，河岸边坡抗滑稳定性安全系数变化如图6所示。

图6 水位升降与坡趾淘刷高度对边坡抗滑稳定性的影响Fig.6 Effect of water level fluctuation and stream erosion height at the slope toe on the slope stability

由图6可知:河床淘刷高度与临坡水位升降对边坡稳定性影响很大。随着淘刷高度的增加，边坡稳定系数逐渐减小;而临坡水位的升降对边坡稳定系数同样起着重大影响，随着临坡水位的升高，边坡稳定系数先减小后增大。

4.2.3 裂隙水位与淘刷深度的影响

临坡河流水位Hr=4.5 m，淘刷切入角度θ0分别取90°，120°，135°，150°，其它条件取值见4.2.1。当张裂缝积水深度Z=0～2 m变化时，河岸边坡抗滑稳定性安全系数变化如7所示。

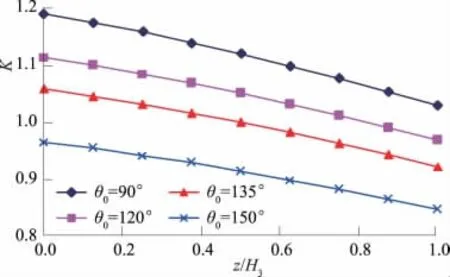
图7 裂隙水位升降与坡趾淘刷切入深度对河岸边坡抗滑稳定性的影响Fig.7 Effect of fissure water level and cutting depth of stream erosion at the slope toe on the slope stability

由图7可知:裂隙水位与坡趾淘刷深度对边坡稳定性影响很大。随着裂隙水位的增加，边坡稳定系数逐渐减小;随着坡趾淘刷切入深度的增加，边坡稳定系数逐渐减小。

4.2.4 裂隙水位与淘刷高度的影响

为更好地说明坡趾淘蚀高度对于边坡稳定性的影响，取θ0=135°。临坡河流水位 Hr=4.5 m，淘刷高度h=H－H2=0～1 m，其它条件取值见4.2.1。当张裂缝积水深度Z=0～2 m变化时，河岸边坡抗滑稳定性安全系数变化如图8所示。

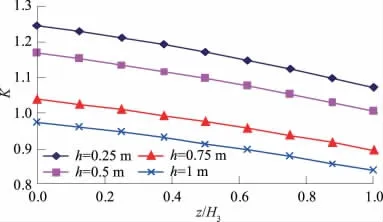
图8 裂隙水位升降与坡趾淘刷高度对河岸边坡抗滑稳定性的影响Fig.8 Effect of fissure water level and stream erosion height at the slope toe on the slope stability

由图7和图8可知:裂隙水位与坡趾淘刷对于河岸边坡稳定性相当不利。若坡体内部排水不通顺，随着裂隙水位的升高，边坡抗滑稳定系数逐渐减少，边坡愈趋于不稳定;坡趾淘刷同样是边坡失稳的重要原因之一，边坡淘刷愈严重，河岸边坡愈趋于不稳定。

5 结论

本文采用极限平衡法，推导了在坡趾淘刷、静水压力、车辆荷载、偶然作用等多因素影响下折线河岸边坡的抗滑稳定系数，得到以下几点认识:

(1)张拉裂缝的产生促进了河岸边坡失稳，裂隙水位是河岸边坡稳定的不利因素，随着张拉裂隙水位的升高，河岸边坡稳定性愈趋于不利。

(2)水位升降对河岸边坡稳定性有着重要影响，临坡水位由高至低的变化过程中，河岸边坡稳定系数先变小再增大。

(3)流水对边坡坡趾的淘刷对于河岸边坡的稳定相当不利，随着坡趾淘刷的高度与切入深度的增加，河岸边坡稳定系数不断减小。

因此，在工程实际中，必须做好坡体内部排水工作，降低裂隙水位，同时应密切关注临坡水位，对于河岸边坡坡趾应做好防冲刷工作，以上工作有利于维持河岸边坡的稳定性。由于土体抗剪强度受水的浸泡影响较大，土体参数遇水软化效应比较复杂，本文尚未考虑，这是以后值得研究的问题。

［1］王延贵，匡尚富.河岸临界崩塌高度的研究［J］.水利学报，2007，38(10):1158－1165.(WANG Yan-gui，KUANG Shang-fu.Critical Height of Bank Collapse［J］.Journal of Hydraulic Engineering，2007，38(10):1158－1165.(in Chinese))

［2］王延贵，匡尚富.河岸淘刷及其对河岸崩塌的影响［J］.中国水利水电科学研究院学报，2005，3(4):251－257.(WANG Yan-gui，KUANG Shang-fu.Study on Bank Erosion and Its Influence on Bank Collapse［J］.Journal of China Institute of Water Resources and Hydropower Research，2005，3(4):251－257.(in Chinese))

［3］赵炼恒，罗 强，李 亮，等.水位升降和流水淘蚀对临河路基边坡稳定性的影响［J］.公路交通科技，2010，27(6):1－8.(ZHAOLian-heng，LUOQiang，LI Liang，et al.Study on Stability of Subgrade Slope along River Subjected to Water Level Fluctuations and Stream Erosion［J］.Journal of Highway and Transportation Research and Development，2010，27(6):1－8.(in Chinese))

［4］赵炼恒，罗 强，李 亮，等.地下水位变化对边坡稳定性影响的上限分析［J］.公路交通科技，2010，27(7):1－7.(ZHAO Lian-heng，LUO Qiang，LI Liang，et al.Analysis of Upper Bound of Slope Stability Considering Ground Water Level Fluctuations［J］.Journal of Highway and Transportation Research and Development，2010，27(7):1－7.(in Chinese))

［5］GRIFFITHSD V，LANEPA.Slope Stability Analysis by Finite Elements［J］.Geotechnique，1999，49(3):387－403.

［6］LANE P A，GRIFFITHSD V.Assessment of Stability of Slopes under Drawdown Conditions［J］.Journal of Geotechnical and Geoenvironmental Engineering，2000，126(5):443－450.

［7］VIRATJANDR C，MICHALOWSKI R L.Limit Analysis of Slope Instability Caused by Partial Submergence and Rapid Drawdown［J］.Canadian Geotechnical Journal，2006，43(8):802－814.

［8］JIA G W，ZHAN L T，CHEN Y M，et al.Performance of a Large-scale Slope Model Subjected to Rising and Lowering Water Levels［J］.Engineering Geology，2009，106:92－103.

［9］马崇武，刘忠玉，苗天德，等.江河水位升降对堤岸边坡稳定性的影响［J］.兰州大学学报，2000，(3):56－60.(MA Chong-wu，LIU Zhong-yu，MIAO Tian-de，et al.The Influence of Water Level Changing on the Stability of River Embankment［J］.Journal of Lanzhou University(Natural Sciences).2000，(3):56－60.(in Chinese))

［10］张均锋，孟祥跃，朱而千.水位变化引起分层边坡滑坡的实验研究［J］.岩石力学与工程学报，2004，23(16):2676－2680.(ZHANG Jun-feng，MENG Xiangyue，ZHU Er-qian.Testing Study on Landslide of Layered Slope Induced by Fluctuation of Water Level［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(16)，2676－2680.(in Chinese))

［11］黄本胜，白玉川，万艳春.河岸崩塌机理的理论模式及其计算［J］.水利学报，2002，33(9):49－60.(HUANG Ben-sheng，BAI Yu-chuan，WAN Yan-chun.Model for Dilapidation Mechanism of Riverbank［J］.Journal of Hydraulic Engineering，2002，33(9):49－60.(in Chinese))

［12］张秀勇.黄河下游堤防破坏机理与安全评价方法的研究［D］.南京:河海大学，2005.(ZHANG Xiu-yong.Study on Failure Mechanism and Methodology of Safety Assessment of the Lower Yellow River Dike［D］.Nanjing:Hohai University，2005.(in Chinese))

［13］王延贵.冲积河流岸滩崩塌机理的理论分析及试验研究［D］.北京:中国水利水电科学研究院，2003.(WANG Yan-gui.Study on Mechanism of Bank Failure in Alluvial River［D］.Beijing:China Institute of Water Resources and Hydropower Research，2003.(in Chinese))

［14］交通部第二公路勘察设计院.公路路基设计手册(第二版)［M］.北京:人民交通出版社，1997.(The Second Highway Consultants Co.Ltd.of the Ministry of Transport.Handbook for Highway Subgrade Design(Second E-dition)［M］.Beijing:China Communications Press，1997.(in Chinese))

［15］李广信.高等土力学［M］.北京:清华大学出版社，2004.(LI Guang-xin.Advanced Soil Mechanics［M］.Beijing:Tsinghua University Press.2004.(in Chinese))

［16］郑颖人.边坡与滑坡工程治理［M］.北京:人民交通出版社，2007.(ZHENG Ying-ren.Slope and Landslide Treatment Engineering［M］.Beijing:China Communications Press，2007.(in Chinese))

［17］NOURI H，FAKHER A，JONES C J.Evaluating the Effects of the Magnitude and Amplification of Pseudo-static Acceleration on Reinforced Soil Slopes and Walls Using the Limit Equilibrium Horizontal Slices Method［J］.Geotextiles and Geomembranes.2008，26(3):263－278.

［18］LOW B K.Reliability Analysis of Rock Slopes Involving Correlated Nonnormals［J］.International Journal of Rock Mechanics and Mining Sciences，2007，44:922－935.