采空区加荷应力场及其多场耦合研究
2012-11-12题正义李宗翔
张 春,题正义,李宗翔
(辽宁工程技术大学 a.安全科学与工程学院;b.矿业学院,辽宁 阜新 123000)
采空区为煤矿灾害的多发区,随着对采空区认识的深入,对其的研究也不断加深,使得采空区的研究变得越来越复杂。目前,对采空区的研究主要应用场耦合理论,如天津城市建设学院的周令昌,辽宁工程技术大学的周西华、李宗翔,西安交通大学的邓军等对采空区温度场进行了研究;华北科技学院的兰泽权、西安科技大学的王红刚等对采空区浓度场进行了研究。有些专家将采空区视为一个复杂的多场系统进行研究,也得到了很多具有实践价值的研究成果,如辽宁工程技术大学李宗翔教授研究了采空区渗流场与氧浓度场之间的耦合,得到了采空区“三带”(采空区内冷却带、自然氧化带、窒息带简称为“三带”)划分为非对称性的结论。焦作工学院的张瑞林等对采空区温度场、风流场及热风压场进行了计算机耦合模拟研究,为采空区煤炭自燃的研究提供了一种新的方法等[1]。虽然采空区的多场耦合研究已经开展得比较深入,但是在多场研究中一直没有考虑采空区加荷应力场的影响,因此,本文主要研究采空区加荷应力场对采空区各场的影响。
1 采空区加荷应力场与各场耦合的理论分析
随着时间的加长,采空区内破碎岩石所承受的应力逐渐加大,最后将趋于原岩应力。由于这种应力是逐渐变大的,因此将采空区内破碎岩石所承受的应力分布状态称为加荷应力场。采空区的加荷应力场主要是通过改变采空区破碎岩石的孔隙率来对其它各场进行影响的。采空区内应力分布的特点决定了采空区内各位置破碎岩石的孔隙率。在采空区内不同的位置,一般应力的大小也不同,从而决定了孔隙率也不相同。大体上是应力大的位置孔隙率小些,应力小的位置孔隙率大些。而孔隙率对前面所提到的各场均有影响,因此,在对采空区进行各场耦合研究时,要考虑到加荷应力场的影响。
在图1[2]中:c'为原岩应力区,此处的应力未受煤层开采的影响,应力值为原岩应力γH;a为支承压力区,即应力增高区,此处的应力值为KγH,高于原岩应力;b为应力降低区,此处的应力值低于原岩应力;c为应力恢复区,此区的应力逐渐由低于原岩应力值恢复为原岩应力值。
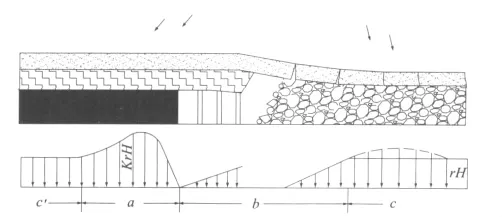
图1 采煤工作面走向顶板应力分布图Fig.1 Stress distribution on the roof of the coal face
根据采煤工作面的状态不同,一般对采空区加荷应力场的研究分为4个阶段:第1个阶段为采煤工作面从开切眼位置到基本顶的初次垮落之前。这段时期煤层的直接顶已经垮落,但上方基本顶的压力对垮落的采空区岩石影响较小。此时采空区内各点孔隙率的大小只需考虑直接顶垮落特点的影响即可。第2个阶段为采煤工作面正常推进阶段。这个时期采空区内各点的孔隙率受到顶板压力的影响,一般认为这种影响是有规律的、呈周期性的变化。在研究此阶段时,只对一个周期进行研究即可。第3个阶段为采煤工作面推进至停采线位置时。第4个阶段为采煤工作面正常推进时,由于一些生产原因工作面停止推进的时期。第4个阶段与第3个阶段较接近,但由于开采未结束,工作面不能进行封闭处理,因此,要对采空区自燃的状况进行研究。由于顶板移动的滞后性,使得此时采空区内的压力分布与正常推进时不同,采空区内破碎岩石的孔隙率分布与正常推进时也不同;这样就会影响采空区内各场,同时顶板压力的变化与采煤工作面的停留时间长短也有关系。本文主要对第4个阶段进行研究。
2 采空区加荷应力场数学模型的建立
2.1 工作面正常推进时期采空区边界加荷应力场与渗透系数的关系
2.1.1 采空区边界加荷应力场的数学模型
当采煤工作面正常推进时,沿着煤层推进方向的上方顶板应力分布如图1所示[2]。从图中可以看出:随着工作面的推进b区可逐渐过渡为c区,同时b区的应力也会逐渐的增加,最后变成c区应力的大小,即原岩应力的大小。采空区内的破碎岩石的碎胀系数随着顶板应力的加大而减小,这也说明了采空区内,尤其是b区内的破碎岩石的渗透系数是变化的。下面对b区内顶板应力分布进行分析。
图2为b区靠近采空区一侧的应力分布示意图,从图中可以看出在此区域的应力满足线性分布。假设此区域的宽度为l,两边界的应力大小分别为0和γH,则距应力为0的边界点x处的应力Px大小为

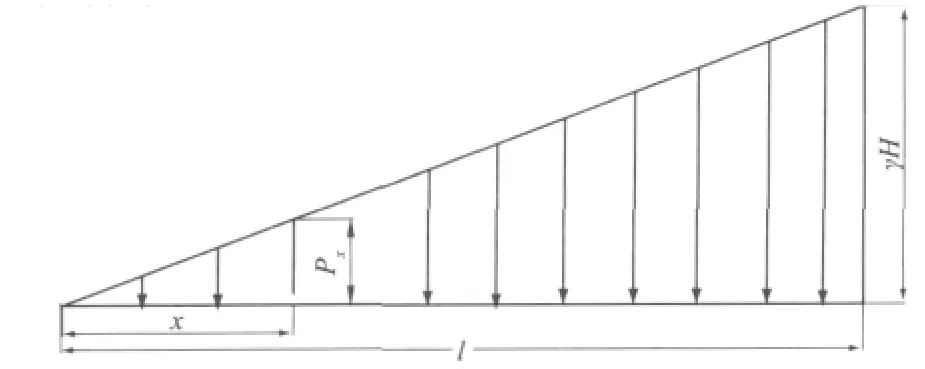
图2 采空区走向边界应力分析图Fig.2 Stress distribution in region b near the goaf side in strike direction
公式(1)为采空区边界内任意一点处的应力大小计算公式。这里仅提到了走向的应力分布问题,对于近水平煤层留煤柱开采时的倾向边界应力大小的计算如图3所示。

图3 采空区倾向边界应力分析图Fig.3 Stress distribution of goaf in dip direction
图3中假设倾向应力降低区的宽度为z;两端边界处应力大小分别为0和Px,则距离煤柱边界y处的应力Pxy大小为

通过图2与图3可以看出采空区倾向边界应力值的大小受采空区走向边界应力的影响,这里对2方向的应力大小进行同时分析的目的在于确定采空区顶点处渗透系数的大小。
2.1.2 采空区边界应力场与破碎岩石压实性关系
采空区破碎岩石在应力增加时碎胀系数将不断减小,最后达到最小值,岩石碎胀系数的大小直接影响到岩石渗透系数的大小。下面分析采空区边界应力值与碎胀系数的关系。
在岩石破碎的初期,破碎岩块间的孔隙较大,碎胀系数大,此时顶板应力稍增加就会使得破碎岩石有很大的收缩量;之后,随着压力的增加岩石的碎胀系数不断减小,破碎岩块之间的作用力逐渐增强,破碎岩块承载能力加大。因此,随着破碎岩块被压密,变形量随着应力的增加不断的减小,最后应力达到最大,不再增加,破碎岩块也停止变形。通过前面的分析,可以得出破碎岩石的碎胀系数与应力的关系接近于负指数函数关系。
假设碎胀系数与应力的关系如式(3)所示:

通过式(3)可以得出采空区边界内任意点的碎胀系数值。
2.1.3 破碎岩石碎胀系数与渗透系数的关系
对于采空区内破碎岩石而言,岩石内的孔隙要比岩块与岩块之间的孔隙小很多。若计算破碎岩石的孔隙率,岩石内部的孔隙完全可以忽略不计,则岩块的孔隙率可以用采空区破碎岩石的碎胀系数表示[3]:

式中:n为破碎岩石的孔隙率;Kp为岩块的碎胀系数。
采空区冒落岩块的非均质性在数值计算方面首先体现在渗透性系数的变化上,关于多孔介质的渗透性系数有许多可以参考的计算公式。这里用式(5)建立多孔介质的渗透性系数k与孔隙率n之间的关系:

式中:k为渗透性系数;Ck为与k同单位的待定系数。
由式(4)空隙率与采空区冒落岩石的碎胀系数Kp的关系,定义用碎胀系数Kp表示的采空区任意位置的渗透性系数为
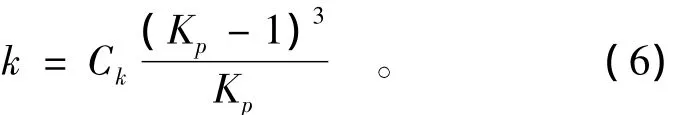
多数研究人员将采空区看成一个二维的多孔介质渗流场。对流场高度是变化的二维平面问题,用KP表达的采空区渗透系数为

式中:K为采空区渗透系数,单位为m3/(Pa·s);H为采空区流场高度;M为开采煤层厚度。
由此可以看出,在采空区内,各个位置的渗透系数是随着破碎岩石的碎胀系数的变化而变化的。因此,可以说采空区是一个非均质的多孔介质流场。
通过前面的分析,得到了采空区应力场与破碎岩石渗透系数之间的关系,而渗透系数是采空区内求取其它各场状态所必须的参数,所以说采空区内的应力场对其它各场存在着影响。但是前面的分析没有考虑到时间的因素,只是应力场对各场静态的影响,只要采煤工作面处于正常推进,这种影响是保持不变的,随着工作面不断前移。若考虑到时间的因素,这种影响就是动态的,下面就分析一下应力场对各场的动态影响。
2.2 工作面停止推进时期的采空区应力场数学模型
顶板的移动要滞后于工作面的开采,当工作面停止开采时,顶板在一定的时间内还要继续的移动、下沉,会使得采空区内的应力恢复区不断地向工作面方向移动,采空区内应力场的分布状态与工作面正常推进时会有很大的不同。下面就来分析当工作面停止推进时采空区的应力场。
在工作面停止向前推进的初期,顶板的移动状态基本没有变化,采空区内的应力恢复区还会以原有的速度向前推进。而随着采煤工作面停滞时间的加长,应力恢复区向前移动的速度不断减小,最后顶板移动停止,采空区内的应力状态不再发生改变。从应力恢复区向采煤工作面推进的过程可以分析出,应力恢复区向前移动的速度服从负指数函数关系。
经过理论分析和推导后,得出应力恢复区向前移动的距离与时间的函数关系如式(8)所示:

式中:L0为自工作面停止向前推进至顶板停止移动期间内应力恢复区向工作面方向移动的最大距离;t0为自工作面停止向前推进至顶板停止移动所需要的时间。
利用绘图的方式,将工作面正常推进时期与停止推进时期的采空区边界应力状态进行对比分析,效果会更加直观,如图4所示。

图4 工作面正常推进与停滞时期采空区内边界应力分布对比图Fig.4 Comparison of boundary stresses in the goaf during normal working period and stagnation period
通过上图可以分析出,随着工作面停滞时间的加长,应力恢复区不断地向工作面方向移动,采空区内边界处的应力逐渐加大。采空区承受应力变大,使得破碎岩石渗透系数随之变小,从而影响到采空区内风流的渗流场以及其他各场。
3 采空区应力场与各场耦合研究的数值模拟
数值模拟方法是依据计算机的编程技术对现场实际条件进行模拟计算,并对所得结论进行研究和分析。它的优点是可重复性强,成本低,危险性小,不影响正常生产,结果较准确。本文中所使用模拟软件为作者应用C++语言开发而成。
依据前面分析结果,以铁法矿务局大平矿某高瓦斯易自燃工作面为例进行模拟研究。工作面长度为200 m,煤层倾角5°,煤厚3.4 m,自燃发火期为20~30 d,计算取采空区走向长度为200 m,采空区最大冒落高度为33 m;供风量为1 200 m3/min,工作面两端总风压差40 Pa。取碎胀系数变化Kp=1.15~1.45,渗透性系数k=0.005~0.107 m3/(Pa·s),待定系数Ck=0.171 6 m2/(Pa·s)。
3.1 应力场与渗流场耦合的数值模拟
应用数值模拟方法对采空区渗流场与应力场的耦合进行模拟,主要通过采空区内渗透系数的变化将其进行耦合研究,模拟结果如图5、图6所示。
由图5的模拟结果可以对比出采空区破碎岩石碎胀系数的变化。随着工作面停滞时间的加长,碎胀系数的梯度变大,同一位置的碎胀系数值变小。同时,在工作面上下两端碎胀系数等值线转弯处,由传统的直角连接变成了弧线连接,这样更贴近实际情况。图5模拟结果与实际现场观测基本相符。

图5 碎胀系数分布模拟Fig.5 Simulation of bulking factor distribution
从模拟图6中可以看出,随着工作面停滞时间的加长、采空区碎胀系数的变化,采空区内漏风较大的区域变小,并在工作面停滞初期,这种变化较大,随着停滞时间增长,这种变化逐渐变小。在采空区内相同位置处漏风量与风速均降低,但在工作面方向采空区边界处,漏风量与风流速度均没有太大变化。其原因为在工作面方向的采空区边界,岩石的碎胀系数随工作面停留时间的变化很小,所以漏风量与风流速度几乎不变,而在采空区内部同一位置处岩石的碎胀系数随着工作面停滞时间的加长而减小,使得通风阻力加大,风流不易流过,因此漏风量与风速变化较大。模拟结果与理论推导结果相符合,与矿井的实际情况也较吻合。

图6 采空区渗流场模拟Fig.6 Simulation of seepage field
3.2 应力场对采空区“三带”划分的影响模拟
采空区“三带”划分是研究采空区煤炭自燃问题中的重点内容,本文也通过模拟的方法来研究分析采空区内应力场对“三带”划分的影响。传统的“三带”划分区域是以采空区中心走向线为对称结构,而辽宁工程技术大学李宗翔教授通过对采空区氧浓度场的分析,得出采空区内“三带”的区域为非对称结构[4-5],本人也比较赞同此观点。因此,本文在模拟研究应力场对采空区“三带”的影响时,主要是研究应力场对非对称结构采空区“三带”的影响。根据前面所提到的条件,对采空区应力场与“三带”耦合研究进行模拟,结果如图7所示。
从模拟图7中可以得出,随着采煤工作面停留时间的加长,冷却带区域变小,自燃带区域向前移动并也变小,窒息带向前移动,但是冷却带范围随时间的变化较小,自燃带区域随时间的变化较大,并逐渐由非对称结构向对称结构转变。其原因为在靠近工作面一侧的采空区边界内,随着碎胀系数的变小,风速较大的区域变小,即冷却带范围变小,但此位置碎胀系数变化较小,所以冷却带范围变化也较小。随着时间的加长,原为冷却带的区域会变为自燃带,因此自燃带有向前移动的趋势,但范围不大;同时由于自燃带碎胀系数的变化较大,自燃带的部分区域会变成窒息带,此区域相对冷却带变成自燃带的区域要大些,所以自燃带范围缩小并程度较大,窒息带要向前移动。随着自燃带范围的缩小,风流在其内部的流程和停留时间均减小,遗煤与采空区中氧气接触的时间也变短,耗氧量下降,这样就会使得采空区倾斜方向的氧浓度差别减小,因此自燃区域会由非对称结构向对称结构转变,但永远不能变成对称结构。

图7 采空区“三带”模拟Fig.7 Simulation of the three zones of the goaf
3.3 应力场对采空区煤炭自燃位置影响的模拟
采空区内遗煤自燃后,燃烧位置的正确判断也是研究采空区煤炭自燃的一个重要内容。采空区内遗煤自燃的位置一般主要根据遗煤氧化的时间及自燃带的特点来进行判断。这里应用模拟的方法来分析研究一下考虑应力后煤炭自燃位置与不考虑应力煤炭自燃位置的差别。模拟结果如图8所示。

图8 采空区自燃位置Fig.8 Simulation of the location of spontaneous combustion taking the effect of stress field into account
由图8可以看出,只要工作面停滞的时间足够长,采空区内的遗煤就能够自燃。并且考虑应力的自燃位置要比不考虑应力时的自燃位置靠近工作面,同时自燃发火期有所增加。其原因为考虑应力的影响时,采空区内自燃带更加靠近工作面,遗煤自燃时也就越靠近工作面,同时由于受应力影响的自燃带着火点要比未考虑应力影响的自燃带着火点与氧气接触的时间短,所以会使得自燃发火期稍稍有所增长。这些模拟结果与理论分析和实践结果都是相符的。
4 结论
通过对采空区应力变化规律、分布特点及其对采空区破碎岩石碎胀系数影响的研究分析后,得到采空区应力与破碎岩石碎胀系数的关系及由于工作面停留而引起的应力变化对采空区内各处碎胀系数变化的影响。根据所分析和研究的应力与碎胀系数的关系,对采空区内的渗流场状态进行了模拟研究,得出了应力场通过改变采空区内各处渗透系数而对采空区内煤炭自燃位置、“三带”划分、流场等的影响。本文的研究结果与实际的观测结果比较接近,与理论分析结果也相符,因此,本文的结论对今后的实践工作具有一定的指导作用。
[1]张瑞林,杨运良,马哲伦,等.自燃采空区风流场、温度场及热力风压场的计算机模拟[J].焦作工学院学报,1998,17(4):253-257.(ZHANG Rui-lin,YANG Yunliang,MA Zhe-lun,et al.Computer Simulation in Spontaneous Combustion Gob’s Air Flowing Field,Temperature Field and Heat Pressure Field[J].Journal of Jiaozuo Institute of Technology,1998,17(4):253-257.(in Chinese))
[2]阎海鹏,张公开,李永明,等.矿压测控技术[M].徐州:中国矿业大学出版社,2007.(YAN Hai-peng,ZHANG Gong-kai,LI Yong-ming,et al.The Measurement and Control Technology of Mine Pressure[M].Xuzhou:China Mining University Press,2007.(in Chinese))
[3]李宗翔.高瓦斯易自燃采空区瓦斯与自燃耦合研究[D].阜新:辽宁工程技术大学,2007:25-28.(LI Zong-xiang.Study of Coupling of Gas and Spontaneous Combustion in Highly Gassy and Spontaneous Combustion Goafs[D].Fuxin:Liaoning Technical University,2007:25-28.(in Chinese))
[4]张 春,题正义,李宗翔.采空区多场耦合的理论研究[J].煤炭技术与工程,2009,18(6):328-331.(ZHANG Chun,TI Zheng-yi,LI Zong-xiang.Research on the Theory of Multi-fields Coupling in Goaf[J].Journal of Coal technical and Engineering.2009,18(6):328-331.(in Chinese))
[5]李宗翔.采空区自然发火“三带”划分的数值模拟[J].辽宁工程技术大学学报,2002,21(5):545-548.(LI Zong-xiang.Study on Numerical Simulation about the Division of Spontaneous Ignition“Three Bands”in Operation Goaf[J].Journal of Liaoning Technical University,2002,21(5):545-548.(in Chinese))
