基于矩阵分裂的预条件SOR迭代法收敛性

雷刚

(宝鸡文理学院 数学系，陕西 宝鸡 721013)

基于矩阵分裂的预条件SOR迭代法收敛性

雷刚

(宝鸡文理学院 数学系，陕西 宝鸡 721013)

对预条件方法解线性方程组，利用黄廷祝等在[“modified SOR-type iterative method for z-matrices”]中提到的预条件能加速SOR迭代法的收敛性，结合矩阵分裂理论及比较定理，给出一种基于矩阵分裂的含参数预条件SOR迭代方法，说明这种方法不仅能加速SOR迭代法的收敛性，而且优于一般的预条件方法，找出参数的最优选取方法，最后通过数值例子加以说明.

预条件；收敛性；SOR迭代法； 谱半径；矩阵分裂

随着计算机的广泛应用，对大型线性方程组的求解大都采用迭代法，但是迭代法的收敛性以及迭代法的收敛速度通常难于把握，近年来都是对线性方程组进行预处理，加速迭代法的收敛性，如何使用预处理以及如何加速收敛速度成为人们关注[1-3]的问题.

1 预备知识

运用迭代法求解大型线性方程组

Ax=b，

(1)

其中A=(aij)n×n∈Rn×n，x，b∈Rn常常都是通过预条件的方法[1-3]加速迭代法的收敛性，也就是给方程组的两边同时左乘一个非奇异矩阵P∈Rn×n，使原方程变为

PAx=Pb.

(2)

为讨论方便，一般假设A=I-L-U为非奇异矩阵(当A为奇异矩阵时，可通过矩阵变换为低阶的非奇异矩阵)，其中I为单位矩阵，-L为严格下三角矩阵，-U为严格上三角矩阵.)

那么，解方程组(1)的SOR(超松驰)迭代法的迭代矩阵为

T=(I-ωL)-1[(1-ω)I+ωU].

(3)

若令M=(I-ωL)，N=[(1-ω)I+ωU]，则SOR迭代矩阵T=M-1N.

常见的预条件因子如文献[1]中提到的P=(I+C)，其中，I为单位矩阵，C为如下形式的方阵

(4)

其中a21，a31，…，an1分别是系数矩阵A=(aij)n×n对应位置上的元素.那么，在预处理因子P=(I+C)作用后，方程组PAx=Pb的系数矩阵记为AC，则

(5)

其中，CL=0，CU=D1+L1+U1；(I-D1)，-(L-C+L1)和-(U+U1)分别是矩阵AC的对角线部分、严格下三角部分和严格上三角部分.从而一般的预处理后的SOR迭代法的迭代矩阵为

TC=[(I-D1)-ω(L-C+L1)]-1[(1-ω)(I-D1)+ω(U+U1)].

(6)

记为TC=MC-1NC.引入参数α，利用矩阵分裂理论，将矩阵AC分裂为

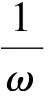
(7)

则改进的SOR迭代法的迭代矩阵为

Tcα=[αI-ω(L-C+L1)]-1[(α-ω)I+ωD1+ω(U+U1)]，

(8)

记为TCα=MCα-1NCα.

2 结论

定义1[4]记所有n×n实矩阵A=(aij)所组成的集合为Rn,n，Rn,n的子集为

Zn,n={A=(aij)|A∈Rn×n,aij≤0，(∀i,j,i≠j)}，

当A∈Zn,n，aiigt;0(∀i)成立时，称矩阵A为L-矩阵.

定义2[5]如果矩阵A能表示为A=sI-B，I为n阶的单位矩阵，B≥0,当s≥ρ(B)时，称A为M-矩阵，特别当sgt;ρ(B)时，称A为非奇异的M-矩阵；当s=ρ(B)时，称A为奇异M-矩阵.其中ρ(B)为B的谱半径.

定义3[6]设方阵A=(aij)的阶n≥2，如果对集合W={1,2,…,n}的任意2个非空不相交的子集S和T，S+T=W，都有i和j满足i∈S,j∈T，使aij≠0，则称A是不可约的，否则称为可约的.

引理1[4](Perron-Frobenius定理)如果A为n阶非负方阵，那么就有

1)A有非负特征值等于其谱半径ρ(A)；

2)A有与ρ(A)相对应的非负特征向量；

3)A的任一元素增加时，ρ(A)不减.

引理2[6]设A为非负矩阵，则

1)若ax≤Ax对某一个非负向量x且x≠0成立，那么就有α≤ρ(A)；

2)若Ax≤βx对某一个正向量x成立，那么就有ρ(A)≤β，进一步，如果A不可约且有0≠ax≤Ax≤βx,ax≠Ax，Ax≠βx对某一个非负向量x成立，则αlt;ρ(A)lt;β.

引理3[3]设A为L-矩阵，满足0lt;ai,i+1ai+1,i,i=1,2,…,n-1，且0lt;ai1a1ilt;1,i=2,3,…,n，那么当0lt;ωlt;1时，由式(3)给出的SOR迭代矩阵T是非负不可约的.

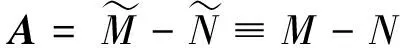
定理1 设T和TCα分别由式(3)和(8)给出的SOR迭代法的迭代矩阵，当线性方程组的系数矩阵A是对角元素为1的L-矩阵，满足0lt;ai,i+1ai+1,i，i=1,2,…,n-1，0lt;ai1a1ilt;1，i=2,3,…,n,且0lt;ω≤α≤1时，就有

1)当ρ(T)gt;1时，ρ(TCα)≥ρ(T)；

2)当ρ(T)=1时，ρ(TCα)=ρ(T)；

3)当ρ(T)lt;1时，ρ(TCα)≤ρ(T).

证明由引理3知，T是一个不可约的非负矩阵，再由引理1知，存在一个正向量x={x1,x2,…,xn}T，满足Tx=λx，其中λ=ρ(T)，即有

[(1-ω)I+ωU]x=(I-ωL)λx.

另外利用CL=0，可得ωCUx=[(λ-1)CI+ωCI]λx.

由A是对角元素为1的L-矩阵，0lt;ω≤α≤1且0lt;αi1a1ilt;1，i=2,3,…,n，结合矩阵L-C+L1是非负的下三角矩阵可知

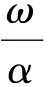
NCα=[(α-ω)I+ωD1+ω(U+U1)]≥0.

考虑

TCαx-λx=MCα-1NCαx-λx=MCα-1(NCα-λMCα)x=

[αI-ω(L-C+L1)]-1{αI-ωI+ωD1+ωU+ωU1-λ[αI-ω(L-C+L1)]}x=

[αI-ω(L-C+L1)]-1{(1-λ)αI+(λ-1)I+(λ-1)C+ωC-λωC+(λ-1)ωL1}x=

[αI-ω(L-C+L1)]-1{(1-λ)αI+(λ-1)I+(λ-1)(1-ω)C+(λ-1)ωL1}x=

[αI-ω(L-C+L1)]-1(λ-1){(1-α)I+(1-ω)C+ωL1}x.

可知TCαx-λx=[αI-ω(L-C+L1)]-1(λ-1){(1-α)I+(1-ω)C+ωL1}x.

令y=[αI-ω(L-C+L1)]-1{(1-α)I+(1-ω)C+ωL1}x，易知ygt;0，结合文献[8]，有

1)如果λgt;1，则TCαx-λx≥0，但TCαx-λx≠0，因此TCαx≥λx，由引理2可得ρ(TCa)≥λ=ρ(T)；

2)如果λ=1，则TCαx-λx=0，因此TCαx=λx，由引理2可得ρ(TCα)=λ=ρ(T)；

3)如果λlt;1，则TCαx-λx≤0，但TCαx-λx≠0，因此TCαx≤λx，由引理2可得ρ(TCα)≤λ=ρ(T).

定理2 设TC和TCα分别由式(6)和(8)给出的SOR迭代法的迭代矩阵，当A为非奇异不可约M-矩阵，满足0lt;αi,i+1αi+1,i,i=1,2,…,n-1，0lt;αi1α1ilt;1，i=2,3,…，n,且0lt;ω≤α≤min{1-αi1α1i}时，就有ρ(TCα)≤ρ(TC)lt;1.

证明由式(7)知

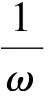
又由于0lt;ω≤α≤min{1-ai1a1i}，L-C+L1是非负的下三角矩阵，结合定理1的证明有

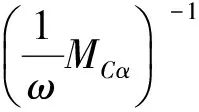
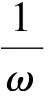
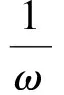
另一方面，由式(5)对AC做如下分裂：

AC=(I-D1)-(L-C+L1)-(U+U1)=

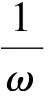
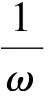
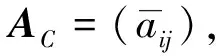
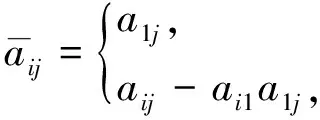
结合条件0lt;ai1a1ilt;1，有I-D1=1-ai1a1igt;0，i=2,3,…,n，0lt;ω≤α≤min{1-ai1a1i}且L-C+L1是非负的下三角矩阵，U+U1是非负的上三角矩阵，从而

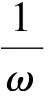
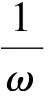
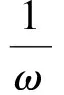
另外，有MCα≠MC，事实上，若MCα=MC，

[αI-ω(L-C+L1)]=[(I-D1)-ω(L-C+L1)]，

即

(1-α)I=D1.

由于0lt;α≤min{1-ai1a1i}，且D1为CU的对角元素组成的方阵，其第1个元素为零，所以这是不可能的，结合条件0lt;α≤min{1-ai1a1i}知，MCα≤MC，从而有MCα-1≥MC-1.

综上，由引理4结合文献[8]可知ρ(TCα)≤ρ(TC)lt;1.

定理3 设T和TCα分别由式(3)和(8)给出的SOR迭代法的迭代矩阵，当A为非奇异不可约M-矩阵，满足0lt;ai,i+1ai+1,i，i=1,2,…,n-1，0lt;ai1a1ilt;1，i=2,3,…,n,且0lt;ω≤αi≤min{1-ai1a1i}时，那么对α1lt;α2，就有

1)当ρ(T)lt;1时，ρ(TCα1)≤ρ(TCα2)；

2)当ρ(T)≥1时，ρ(TCα1)≥ρ(TCα2).

证明由于α1lt;α2，则非负矩阵α1I-(L-C+L1)≤α2I-(L-C+L1)，从而相应的逆矩阵就有[α1I-(L-C+L1)]-1≥[α2I-(L-C+L1)]-1，即MCα1-1≥MCα2-1.

又由定理2知，TCα1是非负矩阵，结合引理1可知其谱半径是它的一个特征值，且有与之相对应的非负特征向量x=(x1,x2,…,xn)T，使得TCα1x=ρ(TCα1)x.所以

ρ(TCα1)x-TCα2x=TCα1x-TCα2x=

MCα1-1(NCα1-λMCα1)x-MCα2-1(NCα2-λMCα2)x≤

MCα1-1[(NCα1-λMCα1)]-(NCα2-λMCα2)x=

MCα1-1(1-λ)(α1-α2)Ix，

即

ρ(TCα1x)-TCα2x≤MCα1-1(1-λ)(α1-α2)Ix.

所以，当ρ(T)=λlt;1，α1lt;α2时，上述不等式右端小于0，从而ρ(TCα1)≤ρ(TCα2)；另一方面，当ρ(T)=λ≥1，α1lt;α2时，同上可知

ρ(TCα1x)-TCα2x=TCα1x-TCα2x=

MCα2-1(λMCα2-NCα2)x-MCα1-1(λMCα1-NCα1)x≥

MCα2-1[(λMCα2-NCα2)-(λMCα1-NCα1)]x=

MCα2-1(λ-1)(α2-α1)Ix.

所以，当ρ(T)=λ≥1时，上述不等式右端大于或等于0，所以ρ(TCα1)≥ρ(TCα2).

推论设TCα是由式(8)给出的SOR迭代法的迭代矩阵，A为非奇异不可约M-矩阵，满足0lt;ai,i+1ai+1,i，i=1,2,…,n-1，0lt;ai1a1ilt;1，i=2,3,…，n，0lt;ω≤α≤min{1-ai1a1i}，那么当ω=α时，由式(8)给出的SOR迭代法的谱半径达到最小.

举例如果矩阵的表达式如下:

则计算可知，以A为线性方程组的系数矩阵，对不同的ω和α时，谱半径的比较如下表1.

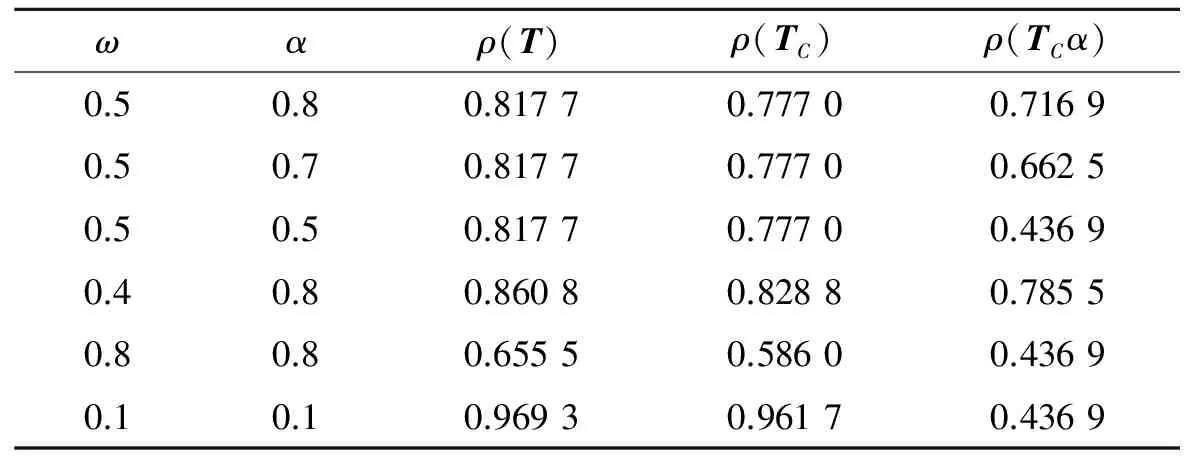
表1 不同参数的迭代法谱半径

从表1可以看出，对给定的ω，文中给出的新迭代法随着α的减小其谱半径也在减小，并且当ω=α时谱半径达到最小；对不同的ω，ω越大，SOR迭代法的谱半径就越小，但是不论ω，α如何变化，都可以得到当ω=α时新的迭代法的谱半径达到最小.

3 结论

理论分析和数值例子显示在新的分裂形式下，谱半径随着参数α的变化可以减小，当ω=α时，该方法的谱半径达到最小，加速收敛的效果优于一般的预条件方法，为大型线性方程组的迭代求解提供新的理论依据.今后可以考虑在加速收敛性的同时适当降低对系数矩阵的要求.

[1] HUANG Tingzhu, CHENG Guanghui, CHENG XiaoYu.Modified SOR-type iterative method for Z-matrices[J].Applied Mathematics and Computation， 2006，175:258-268.

[2] HIROSHi NIKI, KYOUJI HARADA, MUNENORI MORIMOTO，et al.The survey of preconditioners used for accelerating the rate of convergence in the Gauss-Seidel method [J].Journal of Computational and Applied Mathematics， 2004,165: 587-600.

[3] JAE H Y.A note on the modified SOR method for Z-matrices[J].Applied Mathematics and Computation, 2007，194:572-576.

[4] DAVID M Y.Iterative solution of large linear systems[M].New York :Academic Press, 1971.

[5] RICHARD S V.Matrix iterative analysis[M].Spring-Verlag: Heidelberg, 2000.

[6] 张谋成,黎稳.非负矩阵论[M].广州:广东高等教育出版社,1995.

ZHANG Moucheng,LI Wen.Non-negative matrix theory[M].Guangzhou:Guangdong Higher Education Press,1955.

[7] WANG Zhuande, HUANG Tingzhu.Comparison result between Jacobi and other iterative methods[J].Journal of Computational and Applied Mathematics, 2004，169:45-51.

[8] WANG Xuezhong, HUANG Tingzhu，FU Yingding.Comparison results on preconditioned SOR-type iterative method for Z-matrices linear systems[J].Journal of Computational and Applied Mathematics, 2007，206:726-732.

(责任编辑：王兰英)

ConvergencediscussionofSORiterativemethodinpreconditionbasedonmatrixsplitting

LEIGang

( Department of Mathematics, Baoji University of Arts and Sciences, Baoji Shaanxi, 721013,China)

It studies the preconditioned iterative method for the solving the linear system.Ting-Zhu Huang gives the preconditioned to accelerate convergence of SOR iterative method atquot;modified SOR-type iterative method for z-matricesquot;.by using matrix iterative analysis and comparison theorems to make an improved SOR iterative method to solve the large linear system in preconditioned based on matrix splitting, then prove the improved method not only to accelerate the SOR iterative method, but also to excel the general preconditioned SOR method.Last the numerical example is given.

precondition; convergence; SOR iteration method; spectral radius; matrix splitting

O241.6

A

1000-1565(2012)01-0012-05

2011-04-27

国家自然科学基金资助项目(10071048);宝鸡文理学院重点基金资助项目(ZK1031)

雷刚(1977-),男，陕西合阳人，宝鸡文理学院讲师，主要从事数值计算方向研究.

E-mail: lg3048@163.com

MSC2010: 65F10