一种求解非线性二层规划的粒子群算法
2012-11-10朱智慧长江大学一年级教学工作部信息与数学学院湖北荆州434023
朱智慧,陈 忠 (长江大学一年级教学工作部,信息与数学学院,湖北 荆州 434023)
吕一兵 (长江大学信息与数学学院,湖北 荆州 434023)
一种求解非线性二层规划的粒子群算法
朱智慧,陈 忠 (长江大学一年级教学工作部,信息与数学学院,湖北 荆州 434023)
吕一兵 (长江大学信息与数学学院,湖北 荆州 434023)
基于下层问题的K-T最优性条件和罚函数法,结合粒子群算法提出了一种求解非线性二层规划问题的粒子群算法。数值计算结果表明,该算法可以有效地求解非线性二层规划问题。
非线性二层规划;K-T条件;罚函数法;粒子群算法
二层规划是一种具有递阶结构的系统优化问题,其数学模型可以表示为:
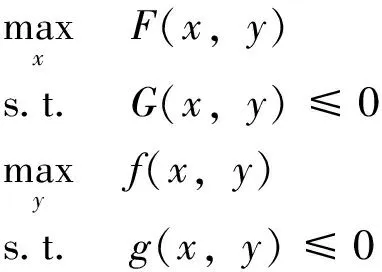
其中,上层决策变量x∈Rn1,下层决策变量y∈Rn2,F(x,y)与f(x,y)分别表示上层目标函数与下层目标函数。线性二层规划的求解是NP难问题,对于非线性规划问题的求解就更加困难,目前的方法主要是集中在求解具有某种特殊结构的非线性二层规划[1],如分支定界法[2]、下降方法[3]以及信赖域方法[4]等。
考虑如下形式的二层二次规划问题:
式中,F(x,y),f(x,y)分别为上层和下层的目标函数,x∈Rn1,y∈Rn2分别为上、下层决策变量;向量c1,c2∈Rn1,d1,d2∈Rn2,b∈Rm;对称矩阵R,Q∈R(n1+n2)×(n1+n2),A∈Rm×n1,B∈Rm×n2。笔者提出了一种求解该类问题的粒子群算法。
1 基本概念

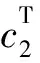
(2)
定义1称集合S={(x,y)|x≥0,y≥0,Ax+By≤b}为二层二次规划问题的约束域;集合P={x|∃y使得(x,y)∈S}是上层决策变量x的可行域。
为了保证问题(1)存在最优解,假设S是非空紧的,Q0为负定矩阵。因此对每个给定的上层决策变量x∈P,下层规划问题存在唯一的解y(x)。
定义2称集合IR={(x,y)|(x,y)∈S,y=y(x)}为二层二次规划问题(1)的可行域。
2 非线性二层规划的粒子群算法
2.1基本粒子群算法
粒子群优化(PSO)算法是一种群智能描述方法,目前已成为演化算法中的研究热点,并广泛应用于其他领域,如神经网络训练、模糊系统控制等应用领域。
PSO算法首先初始化一群随机粒子,每一个粒子都有一个适应度和速度,在每次迭代中,粒子根据本身目前所找到的最优解(个体极值pbest)和整个种群目前找到的最优解(全局极值gbest)更新自己:
vi(t+1)=ω·vi(t)+c1·rand()·(pbesti-xi)+c2·rand()·(gbest-xi)
(3)
xi(t+1)=xi(t)+vi(t+1)
(4)
式中,vi(t)表示第i个粒子在第t次迭代时的速度;xi(t)表示第i个粒子在第k次迭代时的位置;rand()是(0,1)之间的随机数;学习因子c1和c2取2.0;惯性权重ω取值在0.4到0.9之间。文献[5]证明,随着迭代的进行,如果ω从最大惯性权重ωmax线性减小到最小惯性权重ωmin,将显著改善算法的收敛性能。即ω取为:

式中,iter指当前的迭代次数;itermax为算法设定的最大迭代次数。
2.2约束的处理
考虑一般的非线性规划问题:

对于上述问题(5),传统方法的处理方式是将约束优化问题化为无约束优化问题,即将约束条件作为罚项加入目标函数,构造相应的罚问题。然而求解罚问题主要面临如下问题:当惩罚因子过小时得到的解不是原问题的最优解;如果惩罚因子过大会造成数值计算的困难。为此,笔者基于竞争选择策略,设计了特殊的适应度函数来处理约束,即:
(6)
2.3算法
下面,笔者利用改进的粒子群算法求解非线性二层规划问题,其主要思想为:对上层规划问题使用粒子群算法,而利用单纯形法求解下层规划问题。算法的具体步骤如下:
Step 1 随机产生初始粒子群P0,每个粒子的位置表示为zj=(xj,yj)(j=1,2,…,nl),其中,xj表示上层决策变量;yj表示下层决策变量;vj=(vxj,vyj)(j=1,2,nl)表示粒子的速度。
Step 2 设置外层循环次数t=0。
Step 3 更新下层粒子:
①设置初始迭代次数tl=0。
②保持上层决策变量xj不变,更新粒子的位置与速度:
③tl=tl+1。
④如果tl≥Tl转Step 4;否则转①。
Step 4 更新上层粒子:
①设置初始迭代次数tu=0。
②保持下层决策变量yj不变,更新粒子的位置与速度:
③tl=tl+1。
④如果tl≥Tl转Step 5;否则转①。
Step 5t=t+1。
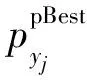
3 数值试验
为了验证所构造粒子群算法的可行性和有效性,考虑如下非线性二层规划问题:

在例1与例2中,取粒子群的规模分别为10与20,最大迭代次数都为50,结果见表1。结果表明,笔者所构造的粒子群算法是有效的。此外,该算法在迭代过程中通过步长控制避免了使用罚函数处理约束带来的困难,并且迭代的过程中没有复杂的计算,实际的程序运行效率较高。

表1 粒子群算法与文献[5-6]结果比较
4 结 语
粒子群优化算法具有收敛速度快、操作简便、需要调整参数少,且对函数性质要求弱的优点。针对上述优点,笔者提出了基于下层问题K-T最优性条件的粒子群算法,以求解非线性二层规划问题,并且在处理约束时,基于竞争选择的概念,设计了特殊的适应度函数,使得迭代点在选择压力下逐渐向可行域靠近,最终靠近最优解。最后,数值试验表明,该算法是可行和有效的。
[1]Deng X. Complexity issues in bilevel linear programming[M].London: Kluwer Academic Publishers, 1998:149-164.
[2]Bard J F. Practical Bilevel Optimization Algorithms and Application[M].London:Kluwer Academic Publishers, 1998.
[3]Vicente L, Savard G, Judice J. Decent approaches for quadratic bilevel programming[J].Journal of Optimization Theory and Applications, 1994,81(2):379-399.
[4]刘国山,韩继业,汪寿阳. 双层优化问题的信赖域算法[J].科学通报, 1998,43(4):383-387.
[5] 盛昭翰. 主从递阶决策论——Stackelberg 问题[M]. 北京:科学出版社,1998.
[6] Mahyar A Amouzegar. A global optimization method for nonlinear bilevel programming problems[J]. IEEE Transactions on Systems, Manamp;Cybernetics-Part B: Cybernetics,1999,29(6): 771-777.
[编辑] 洪云飞
10.3969/j.issn.1673-1409(N).2012.04.001
O224
A
1673-1409(2012)04-N001-03
2012-02-26
国家自然科学基金项目(10926168)。
朱智慧(1982-),男,2002年大学毕业,讲师,硕士生,现主要从事最优化理论与算法方面的教学与研究工作。
