幺正操作算符纠缠的可加性与可乘性

夏慧枝，杨 名，曹卓良

（1.安徽大学 物理与材料科学学院，安徽 合肥 230039；2.合肥师范学院 电子信息工程学院,安徽 合肥 230061）

幺正操作算符纠缠的可加性与可乘性

夏慧枝1，杨 名1，曹卓良2

（1.安徽大学 物理与材料科学学院，安徽 合肥 230039；2.合肥师范学院 电子信息工程学院,安徽 合肥 230061）

联合幺正操作是产生量子纠缠的重要途径。在利用线性熵度量幺正操作算符的算符纠缠，讨论作用到同一量子体系上的多个幺正操作的算符纠缠的可加性和可乘性，并以一般幺正操作和X型幺正操作为例进行具体分析。

联合幺正操作；算符纠缠；可加性；可乘性

量子纠缠在量子信息处理中占据着重要的地位，在很多量子信息过程中，量子纠缠发挥着重要的作用。量子隐形传态过程需要借助于量子纠缠通道传输未知粒子态信息[1]。而量子纠缠交换[2]和量子纠缠纯化[3]过程主要也是利用纠缠粒子对之间的量子纠缠。此外，量子密码学[4]等诸多过程中也都需要量子纠缠。产生量子纠缠的方法有很多。其中，最为常见的一种方法就是利用联合幺正操作产生量子纠缠。目前，有学者发现，当光子在特定条件下进入非中心对称的非线性晶体时(例如BBO晶体)，将以一定的概率自发地分裂为两个较低能量的光子，从而产生具有纠缠特性的量子纠缠光子对[5]。此处，晶体对入射光子的作用可视为幺正操作。通常，我们将满足以下条件的操作称之为幺正操作。

若操作算符U满足：UU+＝U+U＝I (1)则此操作为幺正操作[6]。由此可以看出，幺正操作具有可逆性。

从宏观角度看，当一束光进入光波分束器、棱镜等光学器件，或是一束光由空气入射到水里面时，我们可用幺正算符来描述光束所发生的变化。从微观角度来说，当粒子进入到电磁场或是其他环境当中时，我么也可用幺正算符来描述环境对粒子的作用。通常，我们所关注的系统（如粒子等）会受到多个环境或是场的作用。那么，在多个幺正操作同时对系统实施作用的情况下，系统的纠缠特性与仅仅受到单个幺正操作作用时有何差别和联系呢？对这个问题的探讨有助于我们弄清身处多个环境的实际物理系统的纠缠动力学行为。故对幺正操作叠加性的研究具有重要的理论价值。这里，我们将探讨幺正操作算符纠缠的叠加性，包括其可加性和可乘性。

度量幺正操作算符纠缠能力的算符纠缠有多种，例如冯诺依曼熵、线性熵等等。此处，我们以线性熵度量幺正操作算符的算符纠缠。任意量子态ρ的算符纠缠为 E(ρ)=1-Tr(ρ2)：[7]。 结合算符的施密特分解：任意作用于系统的算符O（幺正或非幺正）可以经过算符施密特分解[8]写为：，{An}和{Bn}分别是系统1和系统2的正交算符基。在此基础上，幺正算符U的算符纠缠可由下式决定[9]：

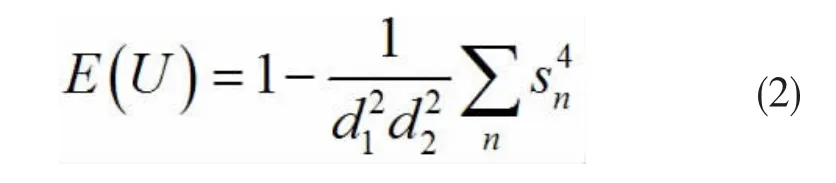
若幺正操作算符U满足：

则称幺正操作算符满足算符纠缠的可加性。若幺正操作算符U满足：

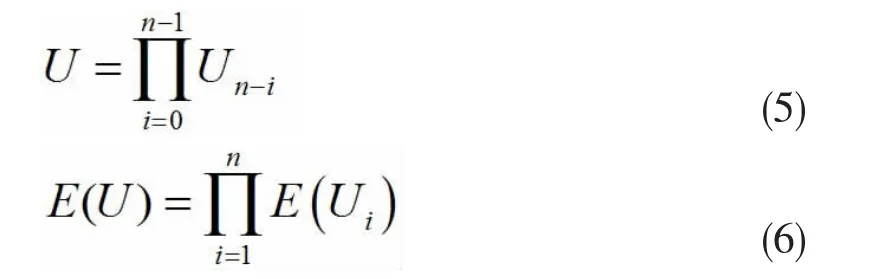
则称幺正操作算符满足算符纠缠的可乘性。

我们将介绍一般控制幺正操作算符和X型幺正操作算符的算符纠缠以及其叠加后的纠缠特性。

1 一般控制幺正操作算符纠缠的叠加特性

对于两粒子的一般控制幺正操作，我们可设其幺正算符为(这里为简单起见，已设相位为零)：

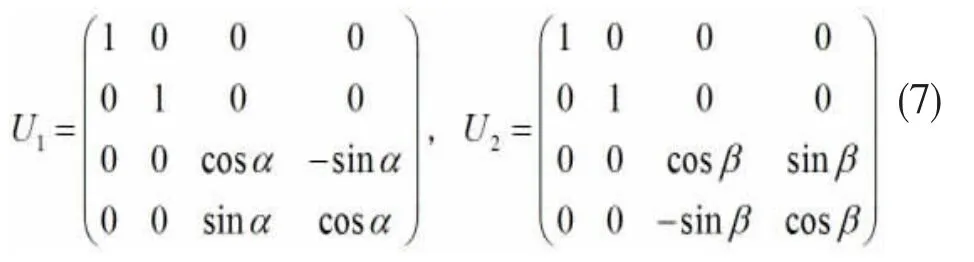
设两粒子所处的初始状态为ρ，经过以上所述的双重幺正操作后，粒子所处的状态为：

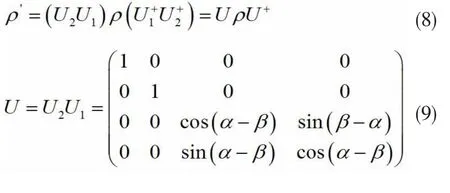
若以线性熵度量幺正算符的算符纠缠，则上述幺正操作算符的算符纠缠分别为：

为便于观察幺正操作叠加前后算符纠缠的关系，我们设：

则可得双重幺正操作算符的算符纠缠为：

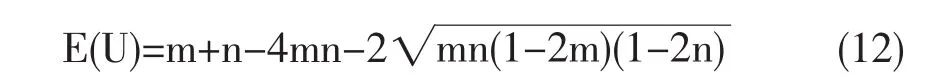
以幺正算符的算符纠缠为坐标，可画出叠加前后算符纠缠关系图，如下所示：

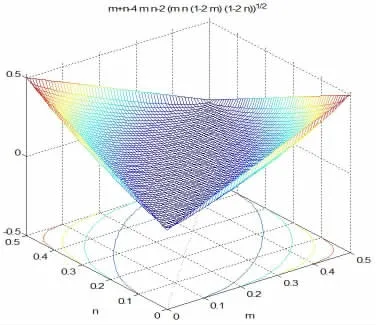
图1 多重幺正操作叠加前后算符纠缠关系图

从上图可以看出，当两个分幺正操作算符的算符纠缠相等时，即m=n，双重幺正操作的叠加为单位阵，则E(U)=E(I)=0。亦证明了幺正操作具有可逆性。另外，一般控制幺正操作算符叠加后，其算符纠缠不具备可加性和可乘性。但是，存在一系列特殊幺正操作算符符合可加性。例如在上图中，以为Z轴，m和n分别代表X和Y轴，曲面分别与XZ和YZ平面交线上的所有幺正操作算符都满足可加性，即E(U)=m+n。在这两条交线上，有一个幺正操作算符为单位阵，其算符纠缠为最小值0，叠加后无影响。

2 X型幺正操作算符纠缠的叠加特性

一般X型（四维）幺正操作算符的矩阵表示为：

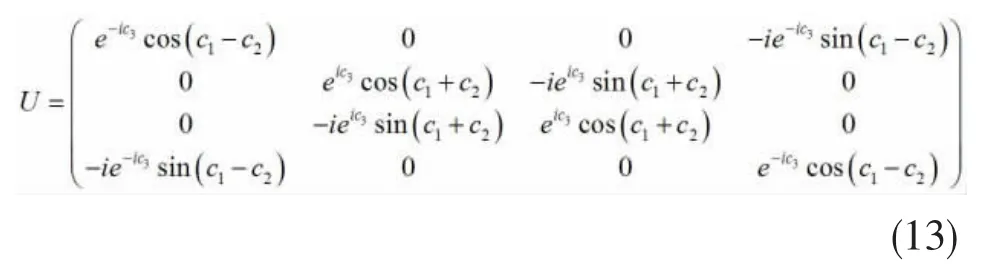
该幺正算符的算符纠缠为：

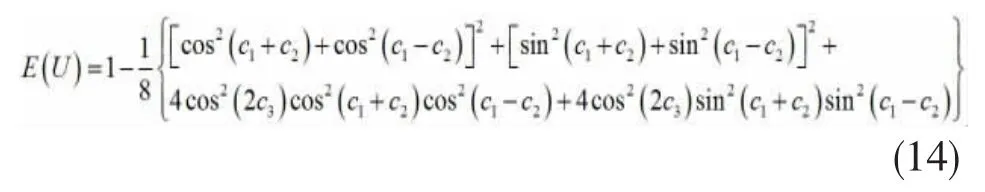
U1和U2为两个一般X型幺正算符矩阵：

两个一般X型幺正操作算符叠加为：

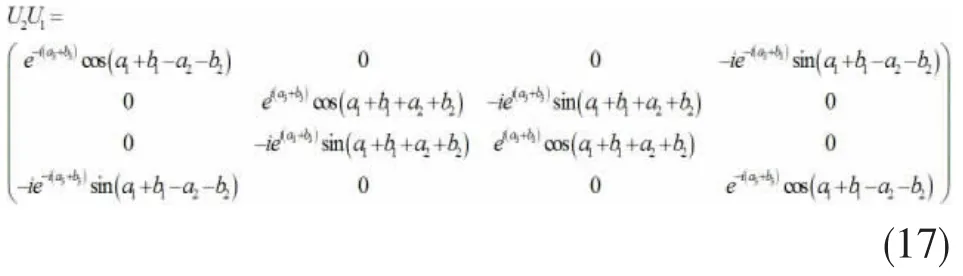
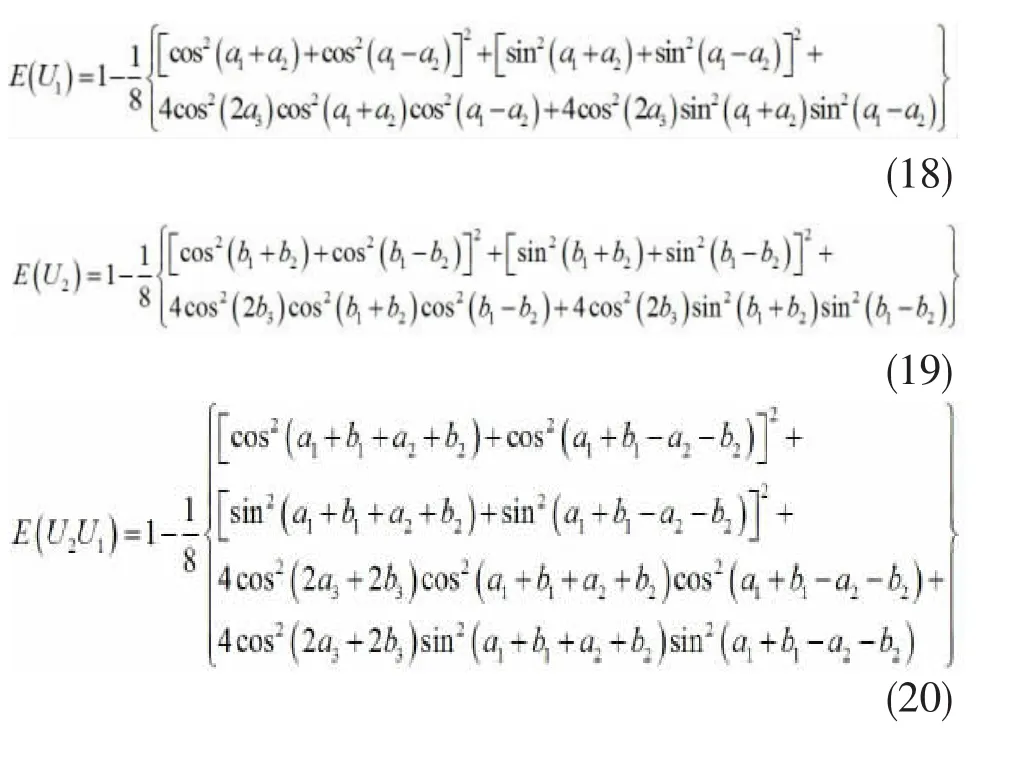
我们分别计算叠加前后幺正操作算符的算符纠缠：将上述两个X型幺正操作算符叠加的理论推广到n个X型幺正操作算符叠加的情况：

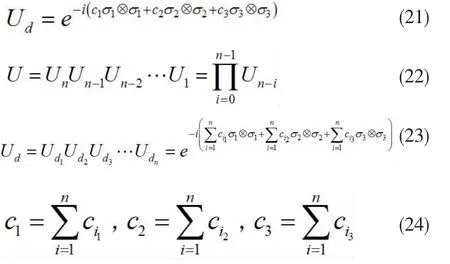
则n个X型幺正操作算符叠加后，其算符纠缠为：

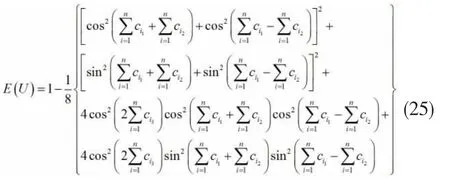
由此，可以看出X型幺正操作算符的算符纠缠也不具备可加性，一些特例除外（例如幺正操作算符为单位阵的情况）。

本文以一般幺正操作和X型幺正操作为例讨论了作用到同一系统上的多个幺正操作的算符纠缠的可加性和可乘性。结果表明，一般联合幺正操作算符的算符纠缠不具备可加性和可乘性，一些特例除外（例如幺正操作算符为单位阵的情况）。

[1]C.H.B ennett,G.Brassard,C.Crepeau,R.Jozsa,A.etc.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J].Phys.Rev.Lett.,1993，70：1895.

[2]M.Zukowski,A.Zeilinger,M.A.Horne,and A.K.Ekert.‘‘Event-ready-detectors’’ Bellexperimentvia entanglement swapping[J].Phys.Rev.Lett.,1993,71:4287.

[3]C.H.Bennett,G.Brassard,S.Popescu,B.Schumacher,J.A.etc.Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels[J].Phys.Rev.Lett.,1996,76:7221.

[4]N.Gisin,G.Ribordy,W.Tittel,and H.Zbinden.Quantum cryptography[J].Rev.Mod.Phys,2002,74:145.

[5]冯瑜，郑小兵，乔延利，等.自发参量下转换机理及应用研究综述[J].量子光学学报，2006,12（2）：0085.

[6]喀兴林.高等量子力学[M].北京：高等教育出版社，2001.

[7]M.Horodecki and M.Horodecki.Information-theoretic aspects of inseparability of mixed states[J].Phys.Rev.,1996:A 54:1838.

[8]M.A.Nielsen,C.M.Dawson,J.L.Dodd,A.Gilchrist,D.etc.Quantum dynamics as a physical resource[J].Phys.Rev.,2003,A 67:052301.

[9]X.-G Wang,B.C.Sanders,and D.W.Berry.Entangling power and operator entanglement in qudit systems[J].Phys.Rev.,2003,A 67:042323.

Additivity and Multiplicativity of Unitary Operations’Operator Entanglement

Xia Huizhi1,Yang Ming1,Cao Zhuoliang2
(1.School of Physics and Material Science,Anhui University,Hefei Anhui 230039;2.School of Electronic information Engineering,Hefei Normal University,Hefei Anhui 230061)

Joint unitary operation is one of important methods to produce entanglement.This paper discusses the properties of multi-unitary operations’operator entanglement in the common quantum system,including the additivity and multiplicativity.Without loss of generality,it analyzes the special case of the general controlled unitary operations and X-type unitary operations.

Joint Unitary Operation;Operator Entanglement;Additivity;Multiplicativity

O413

A

1674-1103(2012)03-0033－03

2012-04-13

国家自然科学基金(10704001、61073048、11005029)；教育部科学技术研究重点项目(210092)；安徽省人事厅学术和技术带头人后备人选择优资助项目。

夏慧枝(1988－),女，安徽庐江人，安徽大学物理与材料科学学院硕士研究生，研究方向为激光物理；杨名(1979－),男，安徽潜山人，安徽大学物理与材料科学学院教授，博士，博士生导师，研究方向为激光物理 。

[责任编辑：桂传友]