湍流模型在单／双缝引射矢量喷管中的验证分析研究

张 强，杨 永

（西北工业大学 翼型、叶栅空气动力学国防科技重点实验室，陕西 西安 710072）

0 引 言

湍流是自然界中普遍存在的一种流动形态。在宏观上，湍流表现为流体微团的不规则运动，湍流运动产生的质量和能量的输运远大于分子热运动所产生的输运，湍流运动引起的质量和能量的平均扩散是不能忽略的。因此湍流研究一直是流体力学研究中的一个重要方向。

国内外针对平板、翼型、机翼等外流标准算例，开展的数值模拟研究已经很多，但针对喷管内流的湍流模型研究主要以Spalart－Allmaras（SA）一方程模型或者改进的k－ε两方程模型为主，其它湍流模型的验证研究还比较少见。现今两方程湍流模型的研究按研究角度主要分为三类：构造k－ε和k－ω的混合模型；构造更为精确的剪应力构成模型；构造新的更准确的耗散方程。其代表模型分别是：SSTk－ω两方程模型，EASMk－ω模型和基于新的耗散方程的k－ζ模型。

国外对射流推力矢量喷管已进行了系统的试验研究［1］，形成了较为完整的数据库，为CFD数值模拟研究提供了良好的条件。因此本文的研究目的就是针对激波控制射流推力矢量喷管的内外流场、喷管性能参数等，分别采用SSTk－ω，EASMk－ω和k－ζ模型，进行系统的验证分析，并与SA模型的计算结果和试验数据进行对比，考察不同湍流模型对喷管内外流场的流场结构、喷管性能参数以及主喷管内壁面的压力分布等的预测能力。之所以选择激波控制射流推力矢量喷管作为验证算例，主要是因为其流场中由于二次射流的干扰，会在主喷流中诱导产生斜激波，存在较强的激波／附面层干扰，这样的流动对目前湍流模型的研究也是一种极大的挑战，因此其数值模拟结果也更具说服力。

1 计算模型及网格

研究激波控制推力矢量喷管时，所采用的模型是NASA LaRC试验用的喷管，设计主流压比为NPRD＝8.78，其几何形状及尺寸见参考文献［2］，单缝引射对应外形1，双缝引射对应外形5。

单缝引射的推力矢量喷管，计算网格如图1所示，图中生成的计算网格共包括5块，包围主喷管的箱体上下各有一块网格，主喷管和次流喷管各生成一块网格，主喷管的出口及箱体上下两块网格的下游，点对点生成一块网格，以计算喷管的尾迹流场。双缝引射喷管外部网格拓扑结构与单缝引射喷管相同，只是在主喷管扩张段上多了另外一个小喷口的网格，如图2所示，并且两个喷口总的开口面积和单缝时的开口面积相同。计算中参考长度取为从主喷管出口到其喉道的长度c，由于喷管总长度为2c，因此后面的喷管无量纲化的长度为2，这样处理以方便与试验值的比较。

图1 单缝引射喷管的计算网格及喷口局部图Fig.1 Computational mesh and close－up of one injection port

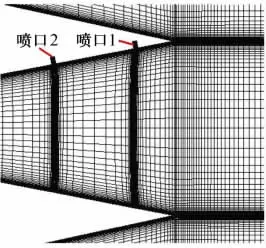
图2 双缝引射喷管的喷口局部图Fig.2 Close－up of two injection ports

2 数值计算方法

针对射流推力矢量喷管的数值模拟，采用的是课题组自有的研究型软件。假定射流推力矢量喷管内外流动是定常的，通过求解不同湍流模型封闭的RANS方程，模拟射流推力矢量喷管的内外流场。RANS流动控制方程的无粘项采用Roe－FDS格式，粘性项采用中心差分，湍流模型的空间项离散也采用二阶迎风格式，流动主控方程和湍流模型的控制方程均采用近似因子隐式时间推进，以提高数值计算效率和稳定性，关于算法的详细介绍可以参考文献［3－5］。

计算条件取为：单缝引射时外流Ma＝0.05，双缝引射时Ma＝0.1，雷诺数Re＝1.65×105，分别采用SA、SSTk－ω、EASMk－ω和k－ζ四种湍流模型求解了主流压比NPR＝4.6，7.0，8.78，10.0和SPR＝0.7、1.0时的射流推力矢量喷管的内外流场。静压固定为标准海平面大气压，总温固定为300K。

3 单缝引射喷管的数值模拟

利用文献［2］的试验结果首先考察了外流马赫数对数值模拟结果的影响，在两个外流马赫数Ma＝0.05及Ma＝0.1下，采用SA湍流模型，模拟了NPR＝4.6、10.0，SPR＝0.7时单缝引射的喷管内外流场。计算的主喷管内壁面压力分布与在静止大气中进行的试验值的比较如图3（a、b）所示，总的来看，在两个马赫数下的数值模拟结果与试验值比较吻合。在两个较小的外流马赫数下，只在NPR＝4.6时，喷管出口截面处的压强略有微小差别，并且我们的数值验证也表明，在这两个马赫数下，喷管性能参数的差别也可以忽略不计，考虑到自由来流马赫数比较小时（例如Ma＝0.05或0.01），流动控制方程不易收敛，为了提高数值计算的稳定性和效率，自由来流马赫数也可以取0.1，对数值模拟结果的影响不大，可以认为它们是相同的。

Ma＝0.05，NPR＝4.6，SPR＝0.7，SA和SSTk－ω模型给出的喷管流场及二次射流局部流场如图4所示，由于二次射流的干扰，在次流喷口之前诱导出现斜激波，在次流喷口上游和下游区域均会出现较大的分离区，两种湍流模型都给出了与试验很接近的激波结构（图5），从EASMk－ω和k－ζ模型的计算结果也可以得出相同的结论。四种模型计算给出的主喷管上壁面，次流引起的斜激波位置都比试验值稍微靠后，约在x／c＝1.62处，而试验测量则是在x／c＝1.543处。

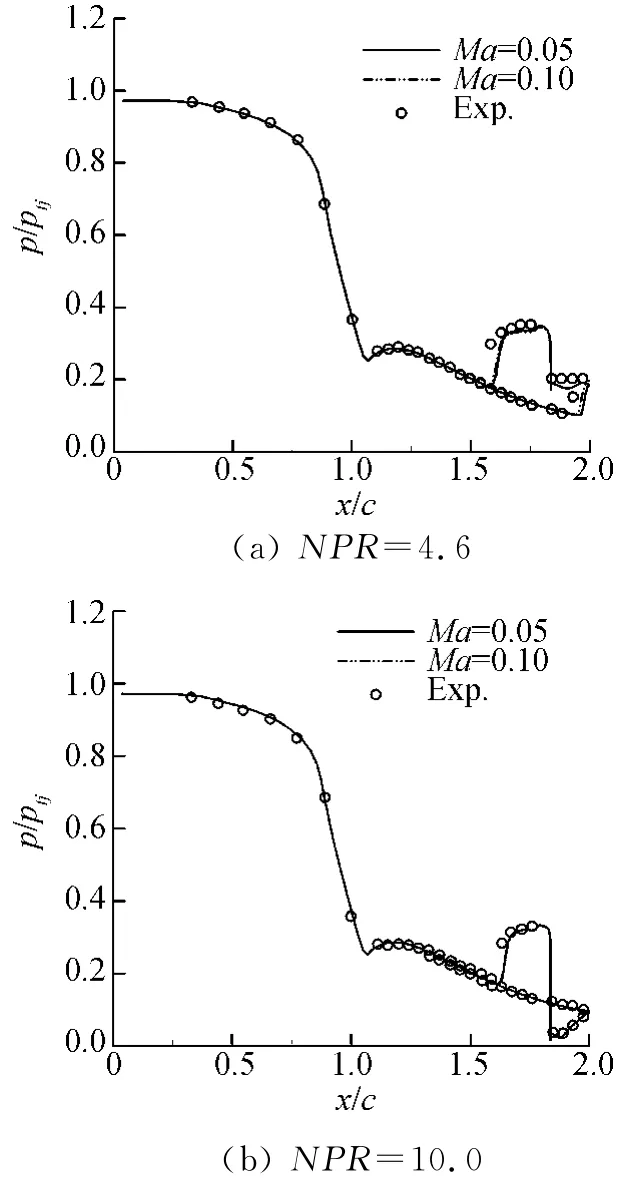
图3 SPR＝0.7，Ma＝0.05和0.1时，SA模型计算的主喷管内壁面压力分布与试验值的比较Fig.3 Experimental and computational pressure distribution at Ma＝0.05，0.1with SPR＝0.7，SA model

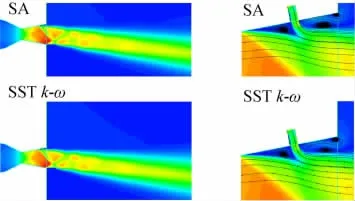
图4 SA和SST k－ω模型计算马赫云图和次喷口局部流场（NPR＝4.6，SPR＝0.7，Ma＝0.05）Fig.4 Mach counters and flow pattern near the injection port for NPR＝4.6，SPR＝0.7，Ma＝0.05with SA and SST model

图5 NPR＝4.6，SPR＝0.7时试验阴影照片Fig.5 Experimental shadowgraph for one injection port，NPR＝4.6，SPR＝0.7

Ma＝0.05，SPR＝0.7，NPR分别为4.6、7.0、8.78、10.0时，主喷管内壁面的压力分布与试验值的对比如图6（a～d）所示。在主喷管下壁面，当NPR＝4.6时，有一段斜激波在喷管内部，SA模型计算的激波位置最靠近出口，其它三种模型给出的激波位置差别不大，但都优于SA模型的计算结果，更接近实验值，从喉道到主喷管出口方向依次是k－ζ，SSTk－ω，EASMk－ω模型，在其他NPR下，下壁面不存在斜激波，四种湍流模型计算给出的压力分布相同，与试验值吻合良好。

在主喷管上壁面，由于二次射流的影响，在次流喷口的上游和下游位置都会出现较大的分离区，二次喷流诱导产生的斜激波位于上游分离区之前，更接近喉道处，在此激波之前主喷管的上壁面，不同NPR下各湍流模型给出的压力分布相同，与试验值完全吻合。在斜激波和次流喷口之间区域，不同NPR下，四种湍流模型给出的激波位置都比试验值略靠后，但压力分布差别不大，仅略低于试验值。在次流喷口以后的区域，受外部回流分离区的影响，不同湍流模型给出的压力分布略有不同，NPR越大，回流分离区越小，各湍流模型的预测越准确。在图6（c）中，当NPR＝8.78时，在主喷管上壁面次流喷口以后的区域，EASMk－ω的结果与试验值差别较大，甚至还不如SA模型，这可能与我们没有考虑流动的非定常效应有关。可见，在有较大分离的区域，四种湍流模型的预测能力还是有差别的。从总的压力分布来看，相比较而言，SSTk－ω模型最 准确，其次是k－ζ和EASMk－ω，SA模型的误差最大。

在SPR＝0.7时，分别采用SA、SSTk－ω、EASMk－ω、k－ζ四种湍流模型计算的射流推力矢量喷管性能参数随NPR的变化如图7所示，不同湍流模型计算给出的喷管性能参数差别不大，随NPR的增加，流量系数几乎保持一个常数，推力系数是先增加后减小，矢量偏角和矢量效率都是一直减小的，与试验得出的规律一致［2］。矢量偏角和矢量效率随NPR的增加减小的原因是：由于二次射流与主喷管流动相互干扰，诱导生成斜激波，随着NPR的增加，受主喷流的影响，斜激波末端逐渐外移，远离主喷管出口，并且强度变弱，导致产生的矢量偏角变小和推力矢量效率降低。

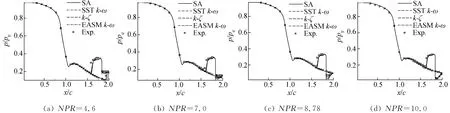
图6 不同NPR下各湍流模型计算的主喷管压力分布（SPR＝0.7）Fig.6 Pressure distribution of the primary nozzle wall for different NPR（SPR＝0.7）

图7 4种湍流模型计算的喷管性能参数（SPR＝0.7）Fig.7 Computational nozzle performance with four turbulence models（SPR＝0.7）

图8是SSTk－ω模型在NPR＝4.6，SPR＝0.7和1.0时计算给出的主喷管上壁面的压力分布，可以看出，在相同NPR下，SPR越大，次流喷口前的激波强度越强，位置越靠近喉道，即随SPR的增加，激波前移，强度增加。不同湍流模型的计算结果均表明，从次喷口进入主喷口的流量与NPR无关，只随SPR的增加而增加。在不同NPR下，SPR＝0.7时，四种湍流模型计算的次喷流流量约是主喷流的4.2%，试验是4%，SPR＝1.0时，次喷流流量约是主喷流的5.7%，试验是6%。

图8 不同SPRSST k－ω模型计算的上壁面压力分布（NPR＝4.6）Fig.8 Pressure distribution of the primary nozzle upper wall with SST k－ω model，NPR＝4.6，SPR＝0.7，1.0

此外，四种湍流模型在SPR＝0.7时，数值计算给出的推力矢量偏角随NPR的变化与试验值的比较如图9所示，各湍流模型的计算结果与试验值吻合良好。在NPR大于4之后，随着NPR的增加，推力矢量偏角变小，与试验得出的结论一致。

4 双缝引射喷管的数值模拟

图9 推力矢量偏角随NPR变化与试验值的比较（SPR＝0.7）Fig.9 SPR＝0.7，Computational thrust vector angle and experiments varying with NPR

双缝引射的喷管，在计算过程中取外流马赫数为0.1，正如我们在前文中所指出的，当马赫数不大于0.1时，外流马赫数对喷管性能的影响很小，可以忽略不计。由于试验中两个次流注入缝是从同一气源引气，因此在数值计算过程中两个次流喷口的入口给定总温、总压边界条件设置相同（即SPR相同），其它边界条件的设定与单缝引射时完全一样。

NPR＝4.6，SPR＝0.7，不同湍流模型给出的喷管及尾迹流场如图10所示，双缝引射会在主喷管中诱导产生两道斜激波，第一道斜激波位于喷口2（图2）之前，第二道斜激波在两个喷口之间，两个喷口左右两侧都会出现分离区，但喷口1两侧的分离区明显大于喷口2，各湍流模型都捕捉到了试验所观测到的激波结构（图11）。四种模型计算给出的主喷管内第一道斜激波的位置都比试验值靠后，约x／c＝1.4处，而试验测量则是在x／c＝1.24处，第二道激波位置与试验相比，k－ζ模型计算给出的激波位置偏靠前，SSTk－ω和EASMk－ω模型与试验值颇为吻合，SA模型给出的激波位置偏靠后，下壁面出口附近的斜激波试验测量在x／c＝1.89处，三种两方程湍流模型的计算结果比较接近，都约在x／c＝1.9处，SA最靠后，约在x／c＝1.94处。

双缝引射的推力矢量喷管，SPR＝0.7时，在一系列NPR下，不同湍流模型计算的主喷管内壁面压力分布与试验值的比较如图12（a～d）所示，总的来看均与试验值吻合良好。双缝引射时第一道斜激波的压力曲线比试验值更陡，激波位置比试验值偏靠后。第二道斜激波处的压力分布比试验值要低，但对激波位置的捕捉要好于第一道斜激波。总体来说，kζ模型计算给出的激波位置最为靠前，SSTk－ω模型次之，之后是EASMk－ω模型，SA模型最为靠后。

图10 不同模型计算的马赫云图（NPR＝4.6，SPR＝0.7）Fig.10 Mach counters for two injection ports nozzle at NPR＝4.6，SPR＝0.7，with different turbulence models

图11 NPR＝4.6，SPR＝0.7时试验阴影照片Fig.11 Experimental shadowgraph for two injection ports，NPR＝4.6，SPR＝0.7

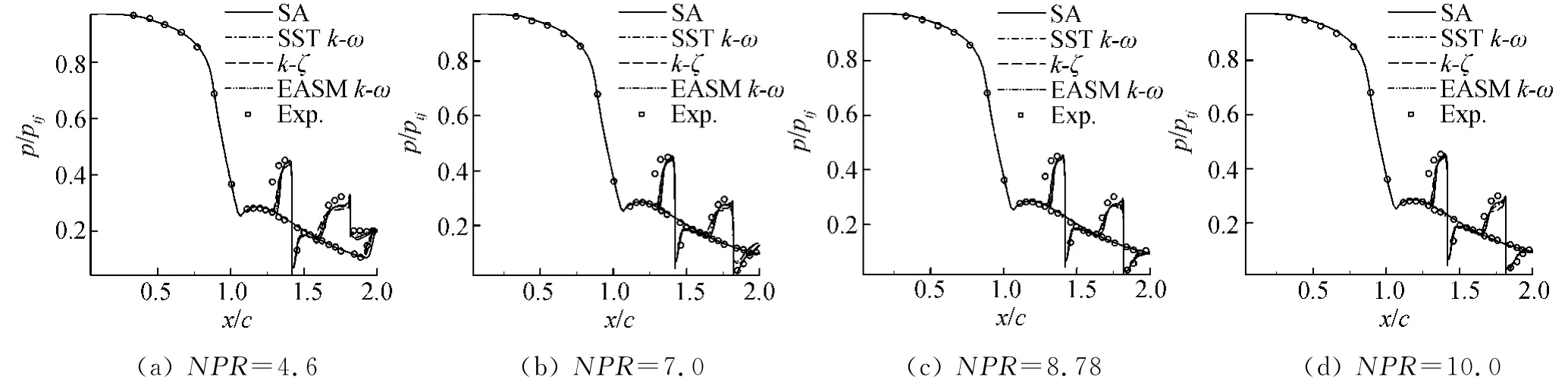
图12 双缝引射喷管上下壁面压力分布与试验值对比Fig.12 Pressure distribution of the primary nozzle wall with two injection ports at different NPR

双缝引射时，不同湍流模型计算的流量系数，推力系数随NPR、SPR的变化规律与单缝引射相同，在此不再赘述。

图13是SPR＝0.7，不同湍流模型计算的双缝引射的推力矢量偏角随NPR的增加与试验值的比较，从图中可以看出，各湍流模型都是在NPR＝4.6时给出了最大的推力矢量偏角，然后随NPR增加，矢量偏角减小。在NPR＝7.0时，SSTk－ω和k－ζ模型计算的推力矢量偏角稍偏大，主要是由于这两种湍流模型过高估计了喷口1后回流分离区的压力，如图12（b）所示，可能是由于此状态下，回流分离区的非定常效应较强，采用定常方法计算，这两种模型无法给出准确的结果。图14是NPR＝4.6，不同SPR下，SSTk－ω模型给出的喷管上壁面压力分布，从图中可以看出，与单缝引射类似，随SPR的增加，两道斜激波的强度增加，位置前移。

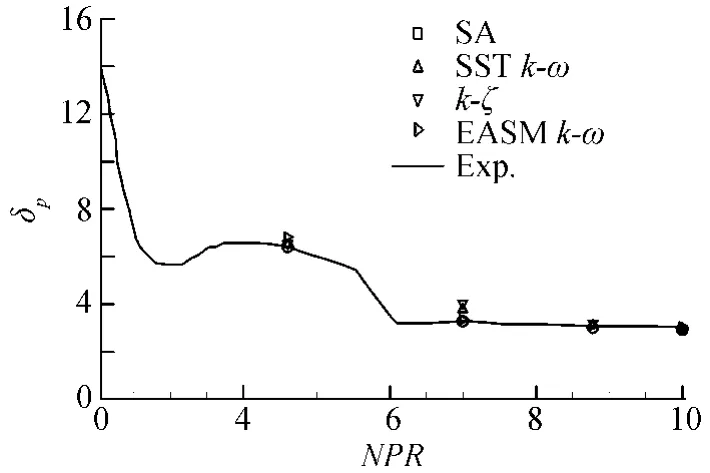
图13 推力矢量偏角随NPR的变化（SPR＝0.7）Fig.13 SPR＝0.7，Computational thrust vector angel and experiments varying with NPR

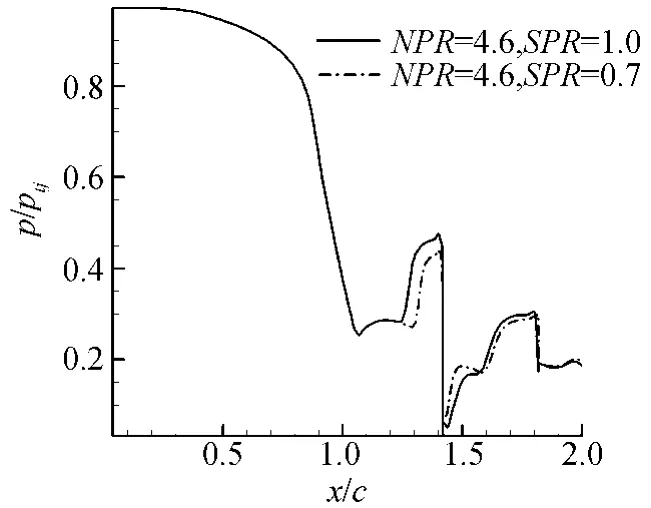
图14 不同SPR下SST k－ω模型计算的上壁面压力分布Fig.14 Pressure distribution of the primary nozzle upper wall with two injection ports，SST k－ω model

5 单／双缝引射矢量喷管性能比较

当SPR＝0.7时，SA湍流模型计算的单／双缝引射喷管性能参数对比如图15所示。双缝引射时，尽管两个次流注入缝总的开口面积与单缝引射喷管相同，SPR也相同，仍然会导致喷管的流量系数降低约1%，在相同的NPR下，推力系数比单缝引射增加了大约1%，利用其它湍流模型的计算结果也可以得出同样的结论。

尽管两个次流注入缝的入口及主喷管入口边界条件设置完全相同（NPR、SPR相同），但由于次流注入缝在主喷管的位置不同，进入主喷管的流量是不同的，靠近主喷管喉道的喷口（喷口2）要比靠近主喷管出口的喷口（喷口1）的流量稍小一些，进入主喷管的总流量也比单缝引射喷管少，减小了约0.7%。

NPR＝4.6，SPR＝0.7时，不同湍流模型给出了在6.4°～6.8°范围内的矢量偏角（试验是6.5°），小于单次流喷口时不同湍流模型给出的介于7.3°～7.6°之间的推力矢量偏角（试验是7.0°），但由于双缝引射时进入主喷管的流量较小，每1%次流注入产生的推力矢量偏角即矢量效率反而是双缝引射大于单缝引射的喷管。在其它NPR下，双缝引射产生的推力矢量效率却比单缝引射小，如图15（d）所示。

图15 SA模型计算的单／双缝引射喷管性能参数比较（SPR＝0.7）Fig.15 Computational nozzle performance with SA turbulence model（SPR＝0.7）

6 结 论

分别采用四种不同湍流模型，通过对激波控制单／双缝引射推力矢量喷管的数值模拟研究分析，可以得出以下结论：

（1）四种湍流模型都能比较准确的预测出单／双缝射流推力矢量喷管的性能参数，并且计算结果差别不大，与试验得出的规律一致。

（2）各湍流模型计算给出的单／双缝主喷管内壁面压力分布均与试验值吻合良好。在激波位置捕捉方面，SSTk－ω、k－ζ和 EASMk－ω模型较好，SA 模型稍差。针对双缝引射喷管，在回流分离区内，SSTkω、k－ζ模型的计算结果并不理想，会过高地估计压力分布。

（3）无论是单缝还是双缝引射，各湍流模型的计算结果均表明，相同NPR，如果SPR增加，进入主喷管的次流流量增加，次流诱导的斜激波前移，主喷管流量系数损失增加，推力系数损失也增加。

（4）双缝引射的推力矢量效率并不一定优于单缝引射。如文中喷管构型，NPR＝4.6时，双缝引射的矢量效率较高，NPR大于4.6时，单缝引射的推力矢量效率较高。

［1］DEERE K A.Summary of fluidic thrust vectoring research conducted at NASA langley research center［R］.AIAA－2003－3800，2003.

［2］KENRIC A W，DEERE K A.Experimental and computational investigation of multiple injection ports in a convergent－divergent nozzle for fluidic thrust vectoring［R］.AIAA－2003－3802，2003.

［3］ZHANG Q，YANG Y。On Exploring predicting precision of an EASMk－ωtwo－equation turbulence model［J］.JournalofNorthwesternPolytechnical University，2005，23（1）：89－92

［4］ZHANG Q，YANG Y.Applying robinson's new twoequationturbulencek－ζmodel to numerically simulating turbulent flow［J］.JournalofNorthwesternPolytechnicalUniversity，2009，27（4）：466－470.

［5］ZHANG Q，YANG Y.Numerical analysis of low reynolds number flow over airfoil［J］.ActaAerodynamic Sinica，2006，24（4）：482－486.