一种新型质量矩飞行器总体布局方案研究

高长生, 姜春旺, 魏鹏鑫, 荆武兴

(哈尔滨工业大学 航天工程系, 黑龙江 哈尔滨 150001)

一种新型质量矩飞行器总体布局方案研究

高长生, 姜春旺, 魏鹏鑫, 荆武兴

(哈尔滨工业大学 航天工程系, 黑龙江 哈尔滨 150001)

针对大气层内非自旋质量矩控制飞行器,提出了一种采用圆环形滑道代替传统的直角正交滑道的布局配置方案。首先,利用牛顿第二定律及动量矩定理建立了基于此布局方案下的飞行器动力学模型,并且得到了弹体动力学的简化模型,通过数值仿真验证了该简化模型的正确性。与直角正交滑道相比,这种圆环形滑道布局的两个滑块可以为系统提供冗余防故障措施,可以大幅度地提高质量矩的控制能力。最后应用最优化理论得出了一种获得期望质心偏移的三滑块位置优化算法,解决了圆环形滑道滑块运动可能产生的碰撞问题。

质量矩飞行器; 圆环形滑道; 控制能力; 最优算法

引言

质量矩控制技术是近年来航天控制领域研究的热点问题[1-3],具有气动布局简单、无舵面烧蚀等优点,因此在大气层内高超声速飞行控制领域具有广阔的应用前景。

在弹头机动方面,俄罗斯已经实现了工程应用,美国也开展了多年研究[4-5]。国外虽然已进入工程实践阶段,但有价值的资料很难获得。国内的质量矩研究主要在导弹总体布局方案、动力学分析和控制律设计等方面。在质量矩控制中,如何设计一个良好的飞行器总体布局是提高系统控制性能的关键[6]。现阶段的总体布局设计主要包括伺服执行机构的设计和活动质量块的配置问题[7]。传统的质量块滑道为直角正交滑道,采用直线电机驱动,可以配置单滑块[8]、双滑块[9-10]以及三滑块[11]。但是,考虑到直角正交滑道布局的质量矩飞行器控制能力有限,为了降低飞行器的成本和重量,提高变质心控制能力,本文提出了一种新型的质量矩飞行器配置方案。

1 系统描述

如图1所示,在飞行器的内部设有圆环形滑道,执行机构采用旋转电机代替直线电机带动质量块运动,这种执行机构无需考虑直线电机运动时运动位置的限制问题。两个质量块可以在旋转电机的驱动下运动到圆环轨道的任意位置。质量块的移动导致了系统质心的改变,在气动外力的作用下获得不同大小的配平迎角,产生期望的升力大小,增强飞行器的弹道机动突防能力。质心偏移产生的力矩也可以用来准确地控制飞行器的姿态机动。

图1 质量矩飞行器结构示意图

两滑块的空间位置变化会使系统质心产生一个大小方向都会变化的系统质心位移。当两滑块的夹角配置为180°时,相当于系统径向质心偏移量为零;当两滑块的夹角很小时,就会提供一个很大的径向质心偏移,这个偏移量是与两滑块夹角有关的一个函数。

在伺服力矩的作用下,飞行器弹体与质量块发生相对旋转运动,通过动量矩交换原理控制弹体绕其纵轴的运动,从而使升力位于所需的过载平面。与以往俯仰和偏航通道采用直线滑道的控制方式不同,质量块的这种角运动可以补偿弹体在飞行时由于热防护结构壳和其他惯性力矩干扰引起的不可避免的滚转运动,达到对控制滚转通道的控制要求。

用两个质量块执行机构就可以提供系统质心的完全变化的能力,进而可以调整飞行器升力的大小。使用两个质量块的另外一个优点在于:两个滑块的存在可以为系统提供冗余防故障措施。当其中一个质量块执行机构失效时,仅仅通过移动另外一个滑块使得两滑块的夹角为180°,就能使系统的配平角为零。这种性能可以很好地保证系统的可靠性。

2 质量矩飞行器动力学模型

本文所建立的变质心飞行器的布局构型如图2所示(视角在飞行器尾部的弹体纵轴截面)。

图2 质量块布局配置剖面图

飞行器由弹体B(质心为b)、滑块p和滑块q组成。图中的滑块(p,q)分别位于垂直于弹体纵轴的圆环形导轨内。任一时刻系统的质心用s表示,建模过程中认为质量块为质点，不考虑其转动特性。各个坐标系的定义如下:

质量块固连坐标系P(Pxpypzp):原点在质量块质心P;Pxp轴平行于飞行器纵轴;Pzp轴在弹体截面原点C与P的连线上,指向弹体外部为正;Pyp由右手定则确定。

质量块固连坐标系Q(Qxqyqzq):原点在质量块质心Q;Qxq轴平行于飞行器纵轴;Qzq轴在弹体截面原点C与Q的连线上,指向弹体外部为正;Qyq由右手定则确定。

另外,体坐标系B(bxbybzb)和惯性坐标系I(OEXIYIZI)的定义见文献[12]。

对公式中的符号定义如下:

弹体B、滑块p、滑块q和系统S的质量之间的关系为:mS=mB+mp+mq;定义滑块p、滑块q的质量比分别为:

μp=mp/mS,μq=mq/mS

(1)

(2)

(3)

(4)

(5)

式中,φ1,φ2分别为滑块p、滑块q与C点连线和弹体bzb轴的夹角。

两个滑块相对于弹体质心b的速度(vbp,vbq)、相对于惯性系的绝对速度(vp,vq)和绝对加速度(ap,aq)分别为:

vbp=ω1×rbp,vbq=ω2×rbq

(6)

vp=vb+ωP/I×rbp,vq=vb+ωQ/I×rbq

(7)

ap=ab+ωP/I×(ωP/I×rbp)+αP/I×rbp

(8)

aq=ab+ωQ/I×(ωQ/I×rbq)+αQ/I×rbq

(9)

式中,rbp,rbq分别为由弹体质心指向滑块p、滑块q的位置矢量,在体坐标系的分量为:

式中,l为滑块p和滑块q的轴向坐标;δ为圆环形滑道的半径。则系统质心s在弹体内的位置矢量为:

rbs=μprbp+μqrbq

(10)

空气动力R1及其力矩MR、地球引力GS和弹体对质心b的转动惯量矩阵IB/b的定义见文献[12]。

基于以上的动力学方程,可以推导出系统的动量Ps为:

Pb=mbvb,Pp=mpvp,Pq=mqvq

(11)

Ps=(mb+mp+mq)vb+ωB×(mprbp+mqrbq)+

ω1×mprbp+ω2×mqrbq

(12)

同理,系统绕质心s的绝对动量矩为:

HS/s=HB/s+HP/s+HQ/s

(13)

其中:

(14)

根据牛顿第二定律和动量矩定理,分别对式(12)和式(13)在惯性系下进行求导,可得弹体平动动力学方程和转动动力学方程为:

(15)

ωB×(IB/bωB)+Mg

(16)

式中,Fp,Fq分别为滑块p和滑块q对弹体施加的惯性力;ΔI为滑块运动引起的转动惯量的变化;Mg为滑块对弹体施加的惯性力矩,其表达式分别为:

Fp=(ωB+ω1)×[(ωB+ω1)×rbp]+

(17)

Fq=(ωB+ω2)×[(ωB+ω2)×rbq]+

(18)

ΔI=-mp[rbp-rbs]×[rbp]×-

mq[rbq-rbs]×[rbq]×

(19)

Mg=-(rbp-rbs)×mp{(ωB+ω1)×

rbp+ωB×ω1×rbp}-(rbq-rbs)×

mq{(ωB+ω2)×[(ωB+ω2)×

(20)

式中,[·]×为该向量的叉乘矩阵。

3 弹体姿态动力学分析与模型简化

将惯性力矩的表达式(20)展开并进行分类,得:

Mg=Mg1+Mg2+Mg3

(21)

弹体姿态旋转和两滑块运动动态特性引起的惯性力矩Mg1的表达式可化简为:

Mg1=-(rbp-rbs)×mp[ωB×(ω1×rbp)+

ω1×(ωB×rbp)+(ωB×ω1)×rbp]-

(rbq-rbs)×mq[ωB×(ω2×rbq)+

ω2×(ωB×rbq)+(ωB×ω2)×rbq]

(22)

仅由滑块运动引起的惯性力矩Mg2的表达式为:

Mg2=-(rbp-rbs)×mp[ω1×(ω1×rbp)+

(23)

由弹体姿态和滑块位置引起的惯性力矩Mg3的表达式化简为:

Mg3=-(rbp-rbs)×mp[ωB×(ωB×rbp)]-

(rbq-rbs)×mq[ωB×(ωB×rbq)]

(24)

设两个滑块的运动规律为在很短的响应时间内运动到指令位置,静止后,可以忽略角φ1,φ2的一阶导数和二阶导数等动态项的影响,即Mg1≈0,Mg2≈0。则方程式(15)和式(16)可以简化为:

msωB×vb

(25)

(IB/bωB)+Mg3

(26)

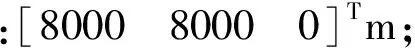
图3 完整模型与简化模型仿真对比

从仿真结果可知:完整模型与简化模型的仿真结果基本一致,迎角和侧滑角的相位和幅值存在着极小的偏差。在控制器设计时,可以用简化模型代替完整模型,符合精度要求。

4 新型布局方式的控制性能分析

对于传统的正交直线布局的滑道,俯仰通道和偏航通道的滑块的直线移动产生了等效质心的移动,如图4(a)所示。而对于本文所提出的圆环形滑道布局的飞行器,在同样条件下,两质量块所产生的等效质心的移动范围要远大于正交直线布局的滑道,如图4(b)所示。

为了更加直观地比较直线正交滑道布局方式与圆环形滑道布局方式的控制能力,下面在相同的参数下进行仿真比较。仿真基本参数与上节相同,设质量块沿直线滑道的最大运动距离δmax=0.1 m,圆环滑道的半径δ=0.1 m。通过仿真比较两种布局方式所能产生的最大迎角和最大法向过载,结果如图5所示。

图4 两种布局方式下的滑块等效质心示意图

图5 两种布局方式的控制能力对比

从仿真结果可以看出,圆环形滑道布局的飞行器控制能力要大于传统的直角正交滑道布局。

从图4(b)可知,由两个滑块就可以产生任何等效位置的质心,但在这样的布局方式下,为了避免两个滑块相撞,其中的一个滑块可能要发生较大的角位移。为了解决这个问题,可以采用三滑块的驱动系统,如图6所示。在三滑块系统中,可以通过操作每个滑块的很小的移动来产生指令质心。下面描述了一种三滑块移动获得期望质心的最优算法。

图6 三滑块的等效质心示意图

设滑块的等效质心坐标为(ye,ze),则该质心位置的运动方程为:

(27)

一个期望的性能指标就是滑块用最小的运动偏移使得系统获得要求的质心偏移。这个性能指标可以表达为:

J=(Δφ1)2+(Δφ2)2+(Δφ3)2

(28)

式中,Δφ1,Δφ2和Δφ3分别为φ1,φ2和φ3的变化量。移动质量块获得一个期望质心的问题实际上是一个在非线性约束条件下的优化问题。这类问题在封闭的形式下很难解决。因此,一个解决途径是将其线性化,然后得到线性化方程的优化方法。由线性化方程式(27),得到质心位置的运动方程如下:

(29)

其中:

(30)

5 结束语

本文提出了一种采用圆环形滑道代替直角正交滑道的布局配置方案,并且建立了基于此布局方案下的飞行器动力学模型,得到了弹体动力学的简化模型。与直角正交滑道相比,这种圆环形滑道布局的两个滑块不但为系统提供了冗余防故障措施,而且可以提高质量矩的控制能力。最后,应用最优控制理论得出了一种获得期望质心偏移的三滑块位置优化算法,解决了圆环形滑道滑块运动的碰撞问题。

[1] Kumar K D,Zou A M.Attitude control of miniature satellites using moving masses [C]//SpaceOps 2010 Conference Delivering on the Dream Hosted by NASA Mars.Huntsville,Alabama,2010:1-6.

[2] 孙卫华,李高风.移动质心再入飞行器姿态的无源性控制[J].宇航学报,2008,29(4):1314-1319.

[3] Mukherjee R M,Balaram J.Attitude dynamics and control of moving mass multibody aeromaneuver vehicle [C]//Atmospheric Flight Mechanics Conference and Exhibit Hosted by AIAA.Honolulu,Hawaii,2008:1-12.

[4] Menon P K,Sweriduk G D,Ohlmeyer E J,et al.Integrated guidance and control of moving-mass actuated kinetic warheads [J].Journal of Guidance,Control,and Dynamics,2004,27(1):118-126.

[5] Byrne R H,Robinett R D,Sturgis B R.Moving mass trim control system design [C]//Guidance,Navigation and Control Conference Hosted by AIAA.San Diego,CA,1996:1-10.

[6] 李瑞康,荆武兴,高长生,等.基于布局优化的飞行器变质心控制性能研究[J].上海航天,2010,(1):9-14.

[7] 姜宇,姚郁,贺风华.一种质量矩飞行器配置方案及其控制问题分析[J].系统工程与电子技术,2008,30(2):320-323.

[8] Robinett R D,Sturgis B R,Kerr S A.Moving mass trim control for aerospace vehicles[J].Journal of Guidance,Control,and Dynamics,1996,19(5):1064-1070.

[9] 廖国宾,于本水,杨宇光.质量矩控制技术的机理分析及方程简化研究[J].系统工程与电子技术,2004,26(11):1635-1639.

[10] 林鹏,周凤岐,周军.基于变质心控制方式的再入弹头控制模式研究[J].航天控制,2007,25(2):16-20.

[11] 张晓宇,贺有智,王子才.质量矩拦截弹的模糊滑模姿态控制系统设计[J].宇航学报,2006,27(6):1419-1423.

[12] 魏鹏鑫,高长生,荆武兴.质量矩控制飞行器的压心不确定性问题研究[J].航天控制,2012,30 (2):39-45.

(编辑：崔立峰)

Researchonanewmethodofgloballayoutformovingmassactuatedvehicle

GAO Chang-sheng, JIANG Chun-wang, WEI Peng-xin, JING Wu-xing

(Department of Aerospace Engineering, Harbin Institute of Technology, Harbin 150001, China)

A scheme of using an annular ring slideway instead of traditional layout of rectangular orthogonal slideway is proposed in this paper for the non-spinning moving mass actuated vehicle within the atmosphere. First of all, the dynamic model is established based on this layout configuration by using Newton’s second law and the moment of momentum theorem. Then the simplified model is derivate and proved correct by numerical simulation. Compared with the rectangular orthogonal slideway, the presence of two moving masses within this annular ring can provide a measure of redundancy and fault-protection, and also can greatly improve the control capacity of moving point masses. Finally, an optimized algorithm that minimizes the movement of the masses to obtain a desirable center of mass is proposed based on optimal control theory. This algorithm solves the slider movement possible collisions of moving masses within the annular ring sildeway.

moving mass actuated vehicle; annular ring sildeway; control capacity; optimal algorithm

V42

A

1002-0853(2012)06-0541-05

2012-03-07;

2012-08-15; < class="emphasis_bold">网络出版时间

时间:2012-11-23 14∶29

国家自然科学基金资助(10902026)

高长生(1978-)，男，黑龙江桦南人，副教授，博士，研究方向为飞行器动力学与控制，导航、制导与控制。