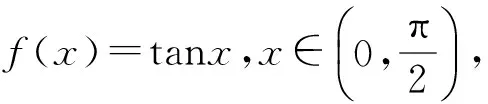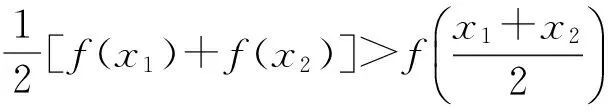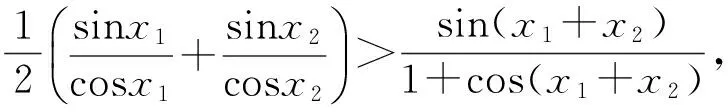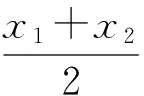转化
——解决高考关键题的灵魂
2012-11-07
●
(海盐元济高级中学 浙江海宁 314300)
转化
——解决高考关键题的灵魂
●胡水林
(海盐元济高级中学 浙江海宁 314300)
综观每年各地高考试题,决胜高考的关键题是选择题、填空题、解答题等各后2个题目,如何处理这6个题目?成败的重要性不言而喻.从浙江省新高考3年来的试题分析,选择、填空题的后4个小题涉及到的知识点每年基本都不一样,有平面向量、立体几何、排列组合、解析几何、集合、函数、方程和不等式等,突出了小题“调头快”的功能,解答题后2个题目固定在解析几何和导函数,涉及到的数学思想丰富.数学思想较之数学基础知识,有更高的层次和地位.它蕴涵在数学知识发生、发展和应用的过程中,是一种数学意识,属于思维的范畴.而这6个题目体现了高中数学的主要思想:数形结合、函数与方程、分类讨论和等价转化,着力体现命题者对于数学思想的关注和重视.而要解好这6个题目的关键是要掌握其灵魂、实施其策略、达到其转化的目的.
著名的数学家、莫斯科大学教授雅洁卡娅曾在一次向数学奥林匹克参赛者发表“什么叫解题”的演讲时提出:“解题就是把要解的题转化为已经解过的题.”数学的解题过程,就是把复杂、生疏、抽象、困难、未知的问题向简单、熟悉、具体、容易、已知问题的化归转换过程.这是一种思想方法,也是一种策略.本文试图用函数与方程、数与形、分类与讨论、等价与化归等四大转化策略探索解决此类问题的方法,与同行们共同探讨之.
1 函数与方程的转化策略
函数思想,是指利用函数的概念和性质去分析、转化和解决问题.方程思想,是从问题的数量关系入手,运用数学语言将问题中的条件转化为数学模型(方程、不等式或方程与不等式的混合),然后通过解方程(组)或不等式(组)使问题获解.更重要的是使函数与方程互相转化,达到解决问题的目的.如:不等式恒成立问题等.
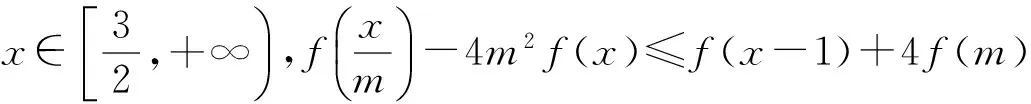
(2010年天津市数学高考理科试题)
分析不等式恒成立问题在近几年高考中经常出现,这类问题既含参变量又含自变量,往往与函数、数列、方程、几何有机结合起来,具有形式灵活、思维性强、知识交汇点多等特点,考题主要有以下2种方式:一是证明某个不等式恒成立,二是已知某个不等式恒成立,求其中的参数的值或取值范围.解决这类问题的关键是转化,通过化归到函数求其最值来处理.
解法1分离变量法
依据题意得
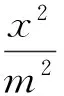
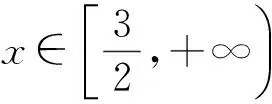
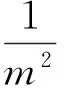
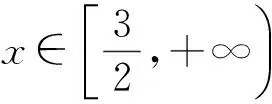
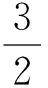
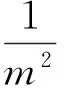
即
(3m2+1)(4m2-3)≥0,
解得
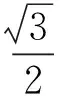
解法2函数法
依据题意得
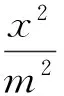
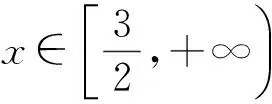
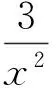
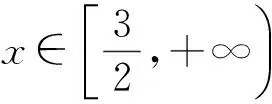
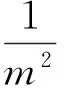
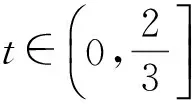
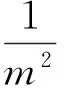
则
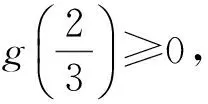
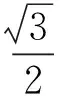
点评本题是较为典型的恒成立问题.解决恒成立问题的第1种解法是利用分离变量为最值的方法求解,即对原有不等式通过分离变量的方法分离出变量式,使其成为f(m)≤g(x),然后求g(x)这个函数的最小值得g(x)≥k(或g(x)>k),从而f(m)≤k.解决恒成立问题的第2种解法是函数法,即通过构造函数,转化利用函数的特性分析解决问题.
变式1若函数f(x)=x4-6x2-(3+a)x在[0,2]上为增函数,求a的取值范围.
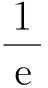
(2010年全国数学高考理科试题改编)
2 数与形的转化策略
数与形是数学中2个最古老、最基本的问题,二者之间是密不可分的.恩格斯曾说过:“数学是研究现实世界中量的关系与空间形式的科学.”数形结合就是根据数学问题的条件和结论之间的内在联系,既分析其代数意义,又揭示其几何直观,使数量关系的精确刻画与空间形式的直观形象巧妙、和谐地结合在一起,充分利用这种结合,寻找解题思路,使问题化难为易、化繁为简,从而解决问题.
纵观多年来的高考试题,把数量关系的问题转化为图形性质的问题则会变抽象为直观,使隐含的关系显露出来.许多代数、三角问题有着几何图形背景,因此绘制其图形来研究问题会显得十分直观.反之,把图形性质的问题转化为数量关系的问题,在一定程度上说,使研究方式程序化.许多几何问题可以利用代数、三角函数的方法解决,显得十分简洁、明确,起到事半功倍的效果.
例2设a,b是2个实数,A={(x,y)|x=n,y=na+b(n∈Z)},B={(x,y)|x=m,y=3m2+15(m∈Z)},C={(x,y)|x2+y2≤144},讨论是否存在a和b,使得A∩B≠φ与(a,b)∈C同时成立.
(1985年全国统一高考数学试题)
分析集合A,B都是不连续的点集,“存在a,b,使得A∩B≠φ”的含义是“存在a,b使得na+b=3n2+15(n∈Z)有解(当A∩B时,x=n=m).再抓住主参数a,b,则此问题的几何意义是动点(a,b)在直线l:nx+y=3n2+15上,且直线与圆x2+y2=144有公共点,但原点到直线l的距离大于等于12.
解由A∩B≠φ得
na+b=3n2+15.
设动点(a,b)在直线l:nx+y=3n2+15上,且直线与圆x2+y2=144有公共点,从而圆心到直线距离
又n为整数,知上式不能取到等号,故a,b不存在.
点评集合转化为点集(即曲线),而用几何方法进行研究.此题属探索性问题,可用数形结合法解,其中还体现了主元思想、方程思想,并体现了对有公共点问题的恰当处理方法.
变式1 已知集合
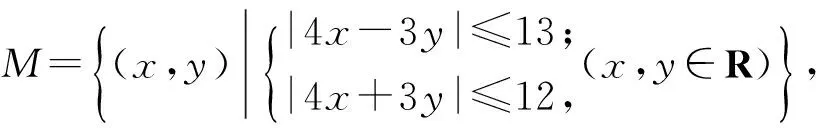
N={(x,y)|(x-a)2+(y-b)2=r2(a,b∈R,r>0)}.
若存在a,b∈R,使得N⊆M,则r的最大值是
( )
A.3 B.2.5 C.2.4 D.2
变式2已知a>c,且ac=-1,则(a+1)2+(c-1)2的最小值为________.
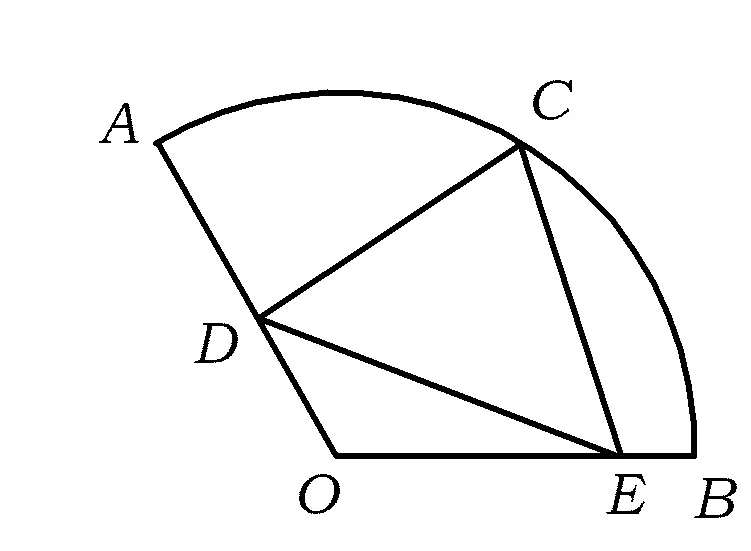
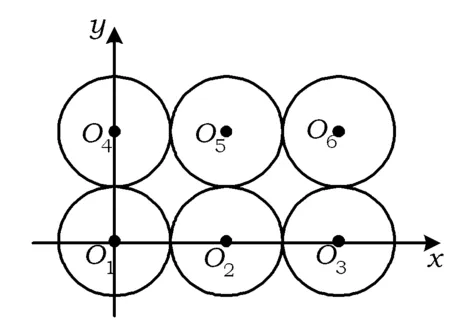
变式3已知0 ( ) A.1个 B.2个 C.3个 D.1个或2个或3个 变式4已知函数f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有4个实数根,则t的取值范围为 ( ) (2012年浙江省数学抽测理科试题) 图1 分析本题是三角题.如令OD=x,OE=y,则将可CD,CE,DE用x,y表示.再令t=OD+OE=x+y,消去y,得到关于x的方程,设函数f(x)并转化为对二次函数的研究. 解法1设OD=x,OE=y,联结OC,则由余弦定理得 CD2=x2+1-x,CE2=y2+1-y, DE2=x2+y2+xy. 4x2+4y2-2x-2y+2xy=1. 令t=OD+OE=x+y,则y=t-x代入消去y得 6x2-6tx+4t2-2t-1=0, 又0 即 解法2也可以利用不等式的性质,由 4x2+4y2-2x-2y+2x=1, 得 4(x+y)2-2(x+y)-1=6xy. 解法3还可以利用换元转化为形.令x=a+b,y=a-b,x≥0,y≥0,则 b≤a,b≥-a,xy=a2-b2, 于是 4(x+y)2-2(x+y)-1=6xy, 可转化为 10a2-4a+6b2=1, 即 求x+y=2a的范围.能满足条件的就是椭圆的一段,则 变式设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是________. (2011年浙江省数学高考理科试题) 分类讨论是一种重要的数学思想方法,当问题所给的对象不能进行统一研究时,就需要对研究对象进行分类,将整体问题划分为局部问题,把复杂问题转化为单一问题,然后分而治之、各个击破,最后综合各类结果得到整个问题的解答.实质上,分类讨论是“化整为零,各个击破,再积零为整”的策略. 图2 图3 例4如图2所示,用6种不同的颜色给图中的4个格子染色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的2个格子颜色不同,则不同的染色方法的种数共有多少种? (2007年天津市数学高考理科试题) 分析按照题设要求,从使用了多少种颜色分类讨论入手,分别计算出各种情形的种类,再用分类计数原理求出不同的染色方法的种数. 解要给图中的4个区域染色,可用2种或3种颜色完成染色任务,故需分成2类: 综上可知,不同的染色方法共有390种. 变式1如图3,用4种不同颜色给图中的A,B,C,D,E,F这6个点涂色,要求每个点涂一种颜色,且图中每条线段的2个端点涂不同的颜色,则不同的涂色方法共有________种(用数字作答). 图4 变式2如图4,有6个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(4,0),O4(0,2),O5(2,2),O6(4,2).记集合M={⊙Oi|i=1,2,3,4,5,6}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称(A,B)为一个“有序集合对”(当A≠B时,(A,B)和(B,A)为不同的有序集合对),那么M中“有序集合对”(A,B)的个数是 ( ) A.50 B.54 C.58 D.60 (2012年浙江省数学抽测理科试题) 等价转化是把未知解的问题转化到在已有知识范围内可解的问题的一种重要的思想方法.通过不断地转化,把不熟悉、不规范、复杂的问题转化为熟悉、规范甚至模式化、简单的问题.历年高考,等价转化思想无处不见,不断培养和训练自觉的转化意识,有利于强化解决数学问题中的应变能力,提高思维能力和技能、技巧. (1994年全国统一高考数学试题) 分析从问题着手进行思考,运用分析法,通过等价转化的方法,逐步探求问题成立的充分条件. 即 cos(x1-x2)<1. 由已知显然cos(x1-x2)<1成立,因此 点评本题在用分析法证明数学问题的过程中,每一步实施的都是等价转化.此种题型属于分析证明型. 变式已知函数f(x)=x2+2x+alnx.当t≥1时,不等式f(2t-1)≥2f(t)-3恒成立,求实数a的取值范围 ( ) A.(-∞,1) B.(-∞,2) C.(-∞,1] D.(-∞,2] (1)求实数a的取值范围; (2)若x1∈(0,1),x2∈(1,+∞).求证: (2012年浙江省数学抽测理科试题) 点评本题主要考查函数极值的概念、导数运算法则、导数应用等基础知识,同时考查推理论证能力、抽象概括等综合解题能力和创新意识. 总之,数学是高考的主要学科,数学成绩的高低将会决定考生的高考命运,而数学试卷上三大类型的后2个题目更是做好全卷的重中之重,能否抓住这关键题的解决灵魂——转化,是决胜数学高考的关键!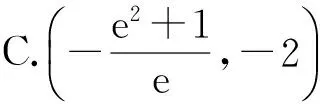
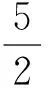
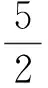
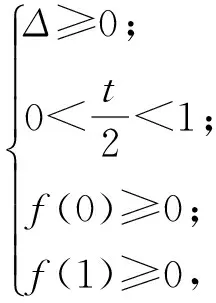
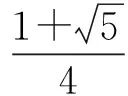

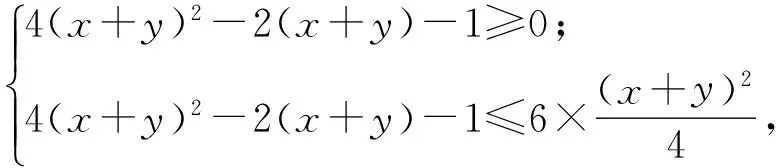
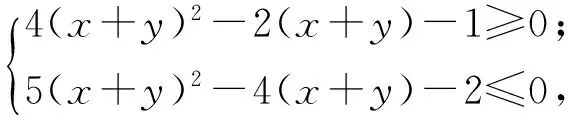
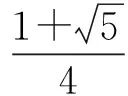
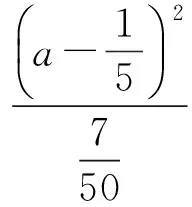
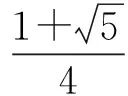
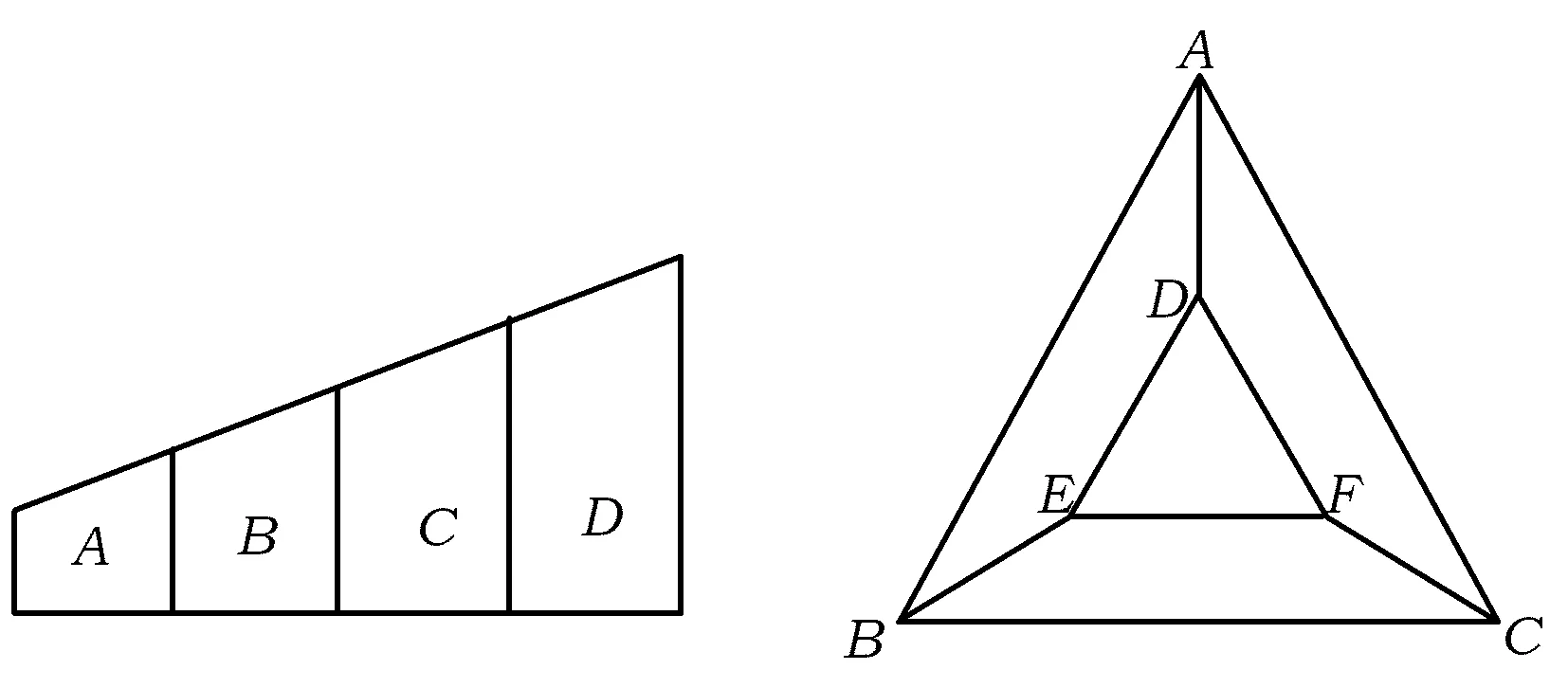
3 分类与讨论的转化策略
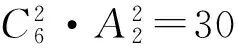
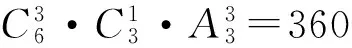
4 等价的转化策略