仿生鱼的运动控制算法设计与仿真实现

杜爽 袁小花

西南科技大学信息工程学院自动化系，四川 绵阳 621000

仿生鱼的运动控制算法设计与仿真实现

杜爽 袁小花

西南科技大学信息工程学院自动化系，四川 绵阳 621000

仿生鱼技术涉及控制学、流体力学、结构物理，材料学等多方面的知识，本文在对鱼类游动形态研究的基础上利用MATLAB软件对鱼类游动模型进行了仿真，并建立了数学模型，推导出了鱼类游动姿态曲线函数，进而设计了运动控制系统。

仿生鱼；舵机；控制系统；MATLAB

引言

鱼类在水中具有游动效率高、机动性能好以及对环境扰动小等优点[1]，仿生鱼技术的研究已经成为仿生机器人方面的热点之一[2]。鱼类推进机理的研究引起越来越多研究者的兴趣，越来越多的理论研究为仿生鱼技术的发展起到了非常重要的作用。如今，仿生机器鱼的研究正朝着多学科结合、多目标任务控制的方向发展[4]。

本文针对以上现象以“波动推进理论”[3]为理论基础，通过MATLAB仿真仿生机器鱼在摆动过程中的姿态曲线，提取了鱼体脊椎的抽象物理模型，同时，以波动推进理论为控制理论结合时序控制算法，实现了仿生鱼的运动控制。

1 仿生鱼物理结构分析

鱼类身体的构造是由于数根脊椎骨连接而成的，所以鱼类摆动的身体可以看成一系列的铰链连接组成的摆链系统。根据波动推进理论[2]的分析，可以提取鱼类摆动部位的结构形态的物理模型，模型中相关参数有:摆动部位占鱼身总长的比例（K），摆动关结数（N），以及各关节之间的长度比例（L1:L2:…:Ln）。K越大游动效率越高，N的大小决定了摆动关节部分的平滑程度，其中各个摆动关节长度之比为如下图1。

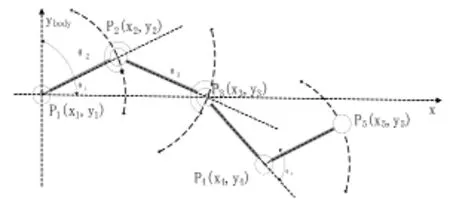
图1 仿生鱼摆动部分铰链式节点轨迹图

在该结构中，关节n的摆动角度θn的范围为0～2π，在笛卡尔坐标系中，假设摆动关节点坐标为 Pn(xn，yn)，则将该坐标系下的关节点坐标转化在极坐标系中，可表示为:

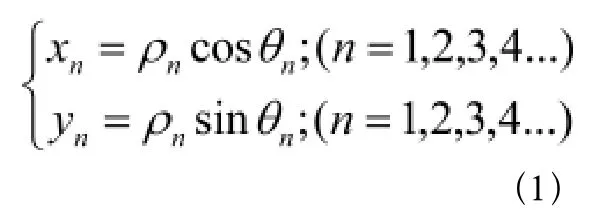
故可以推出得出各个摆动节点的轨迹为:

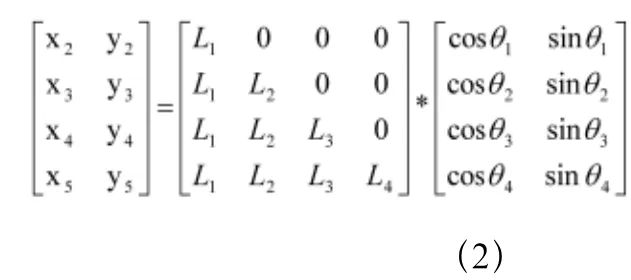
根据以上的关节点坐标，可以通过调节舵机角度θ的值，使得仿生鱼在游动时使流体产分离，并且在尾部产生漩涡。

2 仿生鱼姿态控制分析与仿真

按照波动推进理论， 鱼体波动的形式决定了鱼的游动性能和游动效率。研究人员对各种采用身体波和尾鳍推进方式的鱼类进行了研究， 发现这些鱼类的身体波曲线可以用一个波动方程来表示，Light Hill等人在多年的研究基础上提出的鱼类游动时身体波的方程[3，4，5]表示如下:

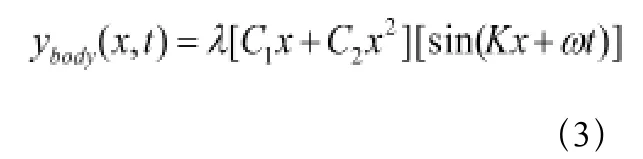
ybody是鱼体的横向位移，x是鱼体的轴向位移；K是体波数K=2π/λ，λ是鱼体波的波长，C1是鱼体波波幅包络线的一次项系数，C2是鱼体波波幅包络线的二次项系数，ω是鱼体波频率(ω=2πf=2π/T)。根据仿生机器鱼的各项物理参数，经过多次的尝试得出了较为理想的摆动曲线方程:

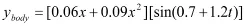
利用MATLAB对该曲线方程进行仿真，如图2:

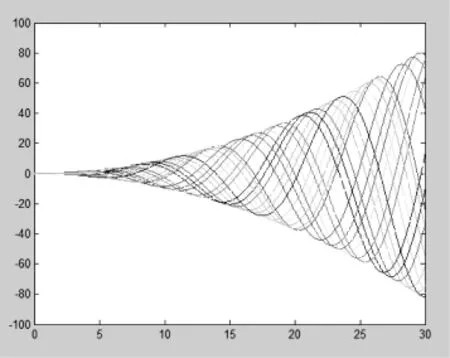
图2 仿真鱼摆动姿态曲线图

根据仿真的姿态曲线，通过对每条姿态曲线进行取样，可以得出图3中的效果图。该图真实的描述了本文设计的仿生机器鱼的摆动轨迹，整体上达到平滑的摆动效果。

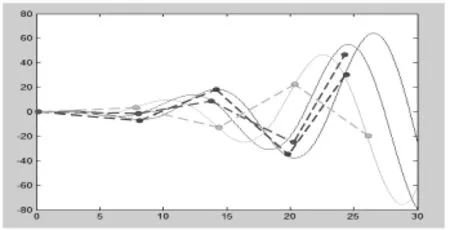
图3 摆动周期内部分关节采样点位置

3、总结

本文对仿生机器鱼的各项参数进行了多次试验，并且所设计控制算法上经过多次的调试，解决了仿生机器鱼在水中的动态平衡问题，基本实现了在模拟仿生机器鱼在水中的游动状态。

本文从仿生机器鱼的机械结构设计上，给出了简化模型的方式，并且根据波动推进理论得出的波动推进曲线，采用取样控制的方案，既结合了摆动过程中的摆动节点的非线性特征，同时也根据柔性鳍波物理模型，提出了控制方案的设计思路。

[1] 张志刚,王硕,桑海泉.仿生机器鱼玩具的机构设计、仿真与实现[J].机器人技术与应用，2004:30～31.

[2] 梁建宏,王田苗,魏洪兴.水下仿生机器鱼的研究进展Ⅰ－鱼类推进机理[J].机器人，2002:107～109.

[3] Light Hill MJ.Aquatic Animal Propulsion of High Hydrom echanical Efficiency.Journal of.Fluids Mechanics，1970.Mech.44:265～301.

[4] 曹长江,张琛,冯建智.多微型机器人系统的协调策略的研究[J].机器人, 2001,23(3): 285～288.

[5] 周志强,王志良等.仿生机器鱼的设计及其运动控制研究[J].微计算机信息，2006:252～259.

[6] 骆涵秀，李世伦，朱捷.机电控制[M].浙江大学出版社，1994:31～63.

TP24

A

10.3969/j.issn.1001-8972.2012.13.074

杜 爽（1990- ）女，西南科技大学信息工程学院，在读本科，主要学习方向:智能控制。