带前后缘控制面机翼的颤振分析
2012-11-06许军马晓平
许军, 马晓平
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
带前后缘控制面机翼的颤振分析
许军, 马晓平
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
针对同时带有前缘和后缘襟翼的二维翼段,研究了考虑不确定性因素的多输入/多输出系统的颤振问题。利用线性分式变换形式,分析了模型中非定常气动力、非线性结构刚度和变结构阻尼等不确定性因素,建立了考虑不确定性的机翼闭环系统状态空间模型。利用鲁棒控制中的μ控制方法,分析了系统的鲁棒性。结果表明,同时带前后缘控制面的机翼可以有效拟制颤振的发生,提高颤振速度达34.96%。
颤振;μ方法; 多控制面; 鲁棒性; 不确定性
引言
现代飞行器设计中的轻质量、高性能要求,使得飞行器气弹问题更加突出。利用主动控制律能够更大程度地改善飞行器的气弹性能[1]。
气动伺服弹性问题已得到重视,特别是有一个后缘控制面气动伺服弹性系统的颤振主动拟制。文献[2-3]的研究基于超声电机作动器的二维翼段颤振主动拟制,分别利用μ方法和H∞方法进行了鲁棒系统稳定性分析。文献[4-6]利用μ方法研究分析了气动伺服弹性系统的稳定性问题。文献[7-9]研究了考虑不确定性的鲁棒颤振拟制。其中文献[8]用鲁棒控制的方法研究了带有前后缘控制面二元翼段颤振的主动拟制问题,并进行了数值仿真和风洞实验,但仅仅研究了考虑翼段扭转刚度和阻尼存在摄动时的反馈线性化自适应控制。对于这种带有前缘控制面的翼段,前缘控制面的偏转使得流场变得更加复杂,控制时更需要考虑气动力模型的不确定性[9]。
本文研究了同时带有前缘和后缘襟翼二维翼段气动伺服弹性的颤振问题。考虑到翼段模型存在非定常气动、非线性结构刚度和变结构阻尼等不确定性,建立了考虑不确定性的机翼闭环气弹模型,利用多变量鲁棒μ方法分析了带有前后缘控制面机翼的鲁棒稳定性问题。
1 带前后缘机翼模型
图1为带前后缘控制面二元翼段的力学模型。前后缘控制面偏角分别为γ,β,翼段的迎角为α,具体相关模型参数均来自文献[8]。

图1 带前后缘二元翼段模型
带有前后缘控制面二元翼段的气弹运动方程如下:
(1)
式中,mT,mW,Ch,Cα,Kh,Kα,L(t)及M(t)分别为机翼前后缘质量、沉浮阻尼、扭转阻尼、沉浮刚度系数、扭转刚度系数以及气动力。对于亚声速流模型,气动力采用准定常气动力模型。
2 不确定性分析
现分析该翼段存在参数摄动情况下的气动力。气动模型中气动力为气动弹性模型的主要摄动变量之一。非定常动压q可描述为定常动压qnom和扰动δq的叠加,即:
q=qnom+δq
(2)
式中,q和δq均为来流速度v、沉浮位移h和弹性轴的迎角α的函数。
将式(2)代入准定常气动力表达式(1)中。设气动力中扰动项分别为w1和w2,其中w1=δqz1=δ1z1,w2=δqz2=δ2z2,化简为:
z1=2bSClββ+2bSClγγ+
(3)
z2=2b2SCmββ+2b2SCmγγ+2b2SCmα×
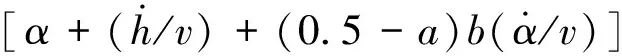
(4)
由于变化粘性阻尼结构非线性引起的沉浮结构阻尼系数为:
Ch=Ch-nom+w3δ3
其中:
w3=e3Ch-nom
则:
Ch=Ch-nom(1+e3δ3)
(5)
式中,w3为沉浮运动的结构阻尼的重量;e3为沉浮运动的结构阻尼重量模型系数;δ3为沉浮运动的结构阻尼摄动。
同理,由于结构非线性引起的俯仰阻尼可表示为:
Kα=Kα-nom(1+e4δ4)
(6)
则扰动输入输出的关系可表示为:
(7)
式中,Δ为扰动矩阵。
因此,考虑摄动的气动力可表示为:
(8)
3 闭环系统
考虑不确定性的多输入多输出鲁棒闭环气弹系统是在多输入多输出开环鲁棒气弹系统上增加了两个反馈控制——后缘控制K1和前缘控制K2,其方框图如图2所示[10]。其中,P为状态空间,输入为前后缘偏角dβ和dγ,输出为沉浮位移h和迎角α,K1和K2分别为反馈函数。多输入多输出的标称系统方框图与图2相比,只是扰动矩阵Δ中少了δ3和δ4两行两列的扰动。

图2 机翼闭环系统模型
4 数值仿真分析
由于前后缘的质量相比机翼质量较小,因此忽略K1和K2减震器的质量,两个减震器的频率为15 Hz。反馈函数K1和K2分别为:


表1 系统相关参数的计算结果
从表1中可以看出,鲁棒闭环系统的颤振临界速度为13.1617 m/s,而带前后缘的鲁棒闭环系统的颤振临界速度为17.7635 m/s,这主要是由前后缘控制面所起的作用。
对各闭环系统在v=13 m/s下进行了数值仿真,结果如图3~图6所示。
图3给出了闭环系统的运动响应历程。对比原闭环系统和带前后缘闭环系统的沉浮和俯仰运动历程可发现:带前后缘控制面的系统相比原系统的俯仰位移和沉浮偏移角都较小,而且拟制需要的时间较短,可见带前后缘系统较原系统有较大优势。
图4和图5分别给出了沉浮和俯仰摄动的Bode图。由图可知,无论对于原系统还是带前后缘的鲁棒系统,沉浮位移h和迎角α对后缘β的影响都比前缘γ影响大。

图3 鲁棒系统运动响应历程

图4 沉浮摄动Bode图

图5 俯仰摄动Bode图
图6为基于μ方法计算的原系统和带前后缘系统的鲁棒稳定边界。通过对比可知,带前后缘系统有较大的优势。

图6 基于μ方法计算的系统稳定边界
5 结束语
本文研究了考虑不确定性带有前缘和后缘控制面二维翼段的颤振问题。通过对系统稳定边界的分析可看出,同时带有前后缘控制面二维翼段有较大的优势。带前后缘闭环系统反馈参数的选择优化将是下一步的研究方向。
[1] 杨超,宋晨,吴志刚,等.多控制面飞机的全机颤振主动拟制设计[J].航空学报,2010,31(8):1501-1508.
[2] 于明礼,胡海岩.基于超声电机作动器的二维翼段颤振主动拟制[J].振动工程学报, 2005,18(4):418-425.
[3] 于明礼,文浩,胡海岩,等.二维翼段颤振μ控制[J]. 航空学报,2007,28(2):340-343.
[4] 吴志刚,杨超.气动伺服弹性系统不确定性建模与鲁棒稳定性[J].航空学报,2003,24(4):312-316.
[5] Wu Zhigang,Yang Chao.A new approach for aeroelastic robust stability analysis[J].Chinese Journal of Aeronautics,2008,21(5):417-422.
[6] Lind R, Brenner M. Analyzing aeroservoelastic stability margins using theμmethod[R].AIAA paper 98-1895,1998.
[7] Waszak M R. Robust multivariable flutter suppression for benchmark active control technology wind-tunnel model[J]. Journal of Guidance,Control,and Dynamic,2001,24(1):147-153.
[8] Platanitis G,Strganac T W. Control of a nonlinear wing section using leading and trailing edge surfaces[J]. Journal of Guidance, Control, and Dynamics, 2004,27(1):52-58.
[9] Borglund D,Nilsson U. Robust wing flutter suppression considering aerodynamic uncertainty[J]. Journal of Aircraft,2004,41(2):331-334.
[10] 梅生伟,申铁龙,刘康志.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2003.
(编辑:姚妙慧)
Flutteranalysisforwingsectionwithleadingandtrailingedgesurfaces
XU Jun, MA Xiao-ping
(National Key Laboratory of Science and Technology on UAV, NWPU, Xi’an 710065, China)
This paper focuses on two-dimensional wing section with leading and trailing edge surfaces. Flutter of a multi-input/multi-output systems is studied. A method to build the state-space model of aeroservoelastic systems is developed based upon linear fractional transformation. The whole aeroservoelastic system is modeled considering uncertainties of unsteady aerodynamic loads, non-linear structural stiffness and variable structure damping,then the model of the close-loop system is constructed by assembling the LFT blocks of the subsystems, the structured singular value is used to analyze robust stability according to theμmethod. The results show that the wing with leading and trailing surfaces can effectively control flutter and increase the flutter speed by 34.96%.
flutter;μmethod; multiple control surfaces; robustness; uncertainty
V215.3
A
1002-0853(2012)05-0402-03
2012-01-10;
2012-04-26
许军(1987-),男,陕西西安人,硕士研究生,主要研究领域为无人机颤振;
马晓平(1961-),男,陕西绥德人,研究员,博士生导师,主要研究领域为无人机总体设计。
