薄壁空心高墩施工阶段顺风向风振响应分析
2012-11-06王振兴高良艳姬志洋
王振兴 高良艳 姬志洋
(河南省第五建筑安装工程集团有限公司,河南郑州 450007)
0 引言
风荷载是作用在结构上的重要动力荷载之一,对于高层建筑结构、高耸结构(高墩、电视塔、烟囱等),有时甚至起决定性作用。
研究风荷载作用下薄壁高墩风振响应分析,除了现场测试、风洞实验方法之外,在理论上主要有两种方法,一种是频域法(Frequency domain),它按随机振动理论,建立了输入风载荷谱的特性与输出结构响应之间的直接关系;另一种是时域法(Time domain),它是基于将随机的风荷载模拟成时间函数,然后直接求解运动微分方程。本文主要通过频域法研究薄壁高墩施工阶段在风载荷作用下的风致振动规律。
1 高墩脉动风基本参数
1.1 工程简介
西张村大桥位于省道S318线石原至三门峡西站段改建工程东段。由于桥区地貌单元为中低山河谷地,水文地质单元为中低山河谷型孔隙、孔隙潜水区,该桥跨越的南北地沟沟深坡陡,其中①~⑥桥墩采用矩形空心薄壁墩,净高分别为57m,68.5m,76m,83m,63m以及43m,其中④墩净高83m,为河南省公路建设历史上的第一高墩,建设技术含量高,施工建造技术复杂。
1.2 脉动风荷载基本参数
根据三门峡西张村大桥的使用功能,结构重要性系数为1.1,设计使用年限为100年,由GTJ/T D60-01-2004公路桥梁抗风设计规范附表A可得,三门峡地区采用重现期为100年,基本风速为27.7m/s,基本风压为0.45kN/m2,表1列出了脉动风速需要的一些基本数据。
根据随机振动理论,在利用频域法分析薄壁高墩顺风向风振响应之前,首先要求出该高度处的平均风速和平均风压。同时,根据薄壁空心高墩施工阶段的结构形式,可以把其计算模型简化为一维多自由度集中质量悬臂体系,薄壁空心墩具有高柔性特性,故将其简化为竖向10个集中质量的计算模型。图1显示了10个集中质量的计算模型的简图。
表2列出了薄壁空心墩集中质量处的平均风速和平均风压。
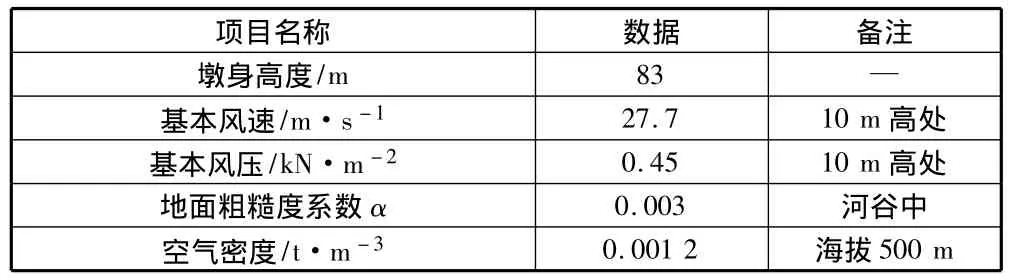
表1 薄壁空心墩脉动风速基本数据
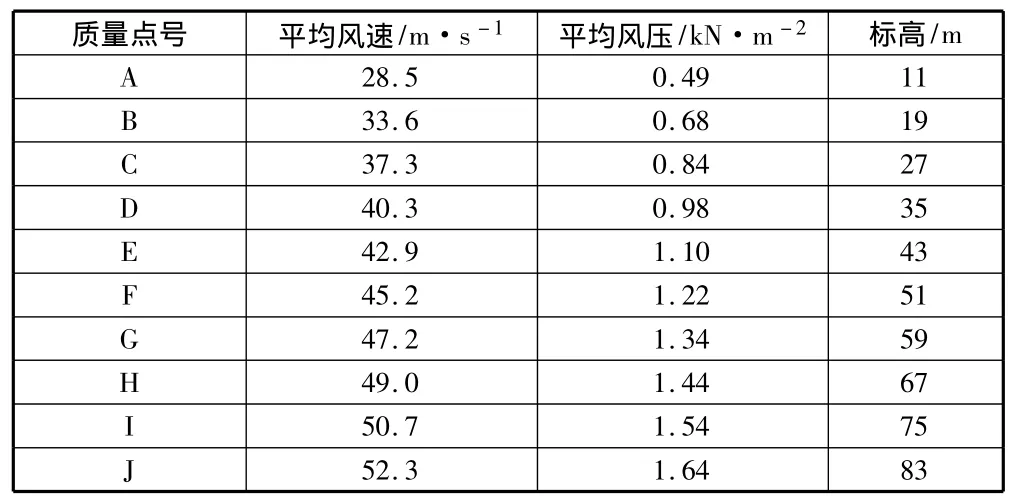
表2 集中质量处的基本风速和基本风压
2 频域内高墩顺风向风振响应分析
2.1 频域法基本理论
频域内计算风振响应的途径,Davenport是这一方法的开创者,他引入了气动导纳和机械导纳的概念,利用气动导纳把风速谱转换到风压谱,利用机械导纳把风压谱转换到响应谱,建立起联系风速资料、结构动力特性和结构响应的桥梁,为结构风效应的研究开辟了道路。
频域内计算响应的基本思想是通过结构的响应传递函数计算响应谱密度。第一步通过位移传函数,即位移导纳来完成;第二步通过数值积和模态叠加来完成。因此该方法也称为功率积分法。

2.2 顺风向风振响应频域分析
施工阶段的薄壁空心高墩可以视为一维的竖向高耸悬臂结构,竖向把高墩简化为10个质量点的多自由度体系。高墩底部为7m×5.128m的矩形,顶部为7m×3.50m的矩形,宽边锥度为0.01,墩高83m。高墩的迎风向为长边,沿高度方向没有变化,高墩底部宽度B0=7m,墩顶宽度BH=7m。
1)薄壁高墩静动力风荷载计算。
墩高H=83m,并根据GTJ/T D60-01-2004公路桥梁抗风设计规范判定高墩属于D类地面粗糙度类别,脉动影响系数n=0.89。
由该高墩的底部宽度B0和顶部宽度BH分别为7m,其比值B0/BH=1.0,则得qv=1.00,并且由表1可以查出该地区的基本风压为0.45kN/m2,由风振系数为
下面把Pi的计算过程列于表3中。

表3 薄壁高墩各点静动力风荷载
由计算结果可知,薄壁空心高墩顺风向墩底设计风荷载弯矩M0为:M0=15931.8kN·m。
如果按照GTJ/T D60-01-2004公路桥梁抗风设计规范规定:桥墩、桥塔、吊杆上的风荷载、横桥向风作用下的斜拉桥斜拉索和悬索桥主揽上的静风荷载可按下式计算:

其中,e为空气密度,ρ=0.0012t/m3;Vg为静阵风风速,可以按照距离地面0.65倍的墩高处的风速值确定,Vg=GVVZ=1.56×45.9=71.6m/s,GV为静阵风系数,桥墩自立阶段按照水平加载长度小于20m选取,故GV=1.65,VZ为基准高度Z处的风速,VZ=V10× (Z/10)0.3=27.7 × (54/10)0.3=45.9m/s;CH为桥墩阻力系数,根据桥墩的截面形状和高宽比,可以求得其值为2.0;An为桥墩顺风向投影面积,An=83×7=581m2。
通过风振系数法计算的墩底弯矩与桥梁静阵风法计算的墩底弯矩比较发现,两者相差72.9kN·m,误差为0.46%,两种方法计算结果非常接近,说明按照风振系数法和桥梁静阵风法计算高墩顺风向风振响应都能满足要求,并且误差很小。
2)薄壁高墩墩顶位移计算。
首先采用风振系数法计算墩顶位移,把风振系数法静动力风荷载计算结果,各质量点静动力风荷载施加在各质量点处,按照结构力学知识计算出各质量点顺风向最大静位移。其次用桥梁静阵风法计算墩顶位移,把桥梁静阵风荷载施加在0.65倍墩高处,计算各质量点顺风向最大静位移。两种方法的计算结果见表4。对比两种方法的墩身位移计算结果可知,虽然桥梁静阵风法结果略大,但二者计算结果非常接近,证明两种计算方法都适用顺风向高墩风振响应的计算。

表4 薄壁高墩位移计算结果
3 结语
本文利用风振系数法和桥梁静阵风法计算了薄壁空心高墩施工阶段顺风向风振响应,得出如下结论:
1)两种计算方法难易程度相当;
2)两种方法计算结果对比表明,误差很小,都可以适用于此类结构相同荷载条件下的计算;
3)虽然频域内的方法适用于此类结构计算,但要想精确分析脉动风对结构产生的响应,还需采用时域方法。
[1]GB50009-2001,建筑结构荷载规范[S].
[2]GTJ/T D60-01-2004,公路桥梁抗风设计规范[S].
[3]张相庭.工程结构风荷载理论和抗风设计手册[M].上海:同济大学出版社,1990.
[4]黄本才.结构抗风分析原理及应用[M].上海:同济大学出版社,2001.
