锦屏大理岩卸荷本构模型与数值模拟研究

李新平，赵 航,，肖桃李,

(1.武汉理工大学 道路桥梁与结构工程重点实验室，武汉 430070；2.武汉理工大学 土木工程与建筑学院，武汉 430070；3.长江大学 城市建设学院，湖北 荆州 434023)

1 引 言

岩石在试验过程中所表现出的力学特性与其所处的应力状态密切相关，加载与卸载是两种不同的应力状态，因此，岩石在加载、卸载两种不同应力路径下的屈服条件、力学参数以及研究方法都是不同的。目前加载岩体力学的研究相对而言比较成熟，而对于卸荷岩体力学的研究还有大量的工作要做。

Swanson等[1]利用常规三轴实验设备，研究了卸围压对岩石强度的影响，认为岩石强度与应力路径并无关系。陶履彬等[2]对花岗岩试件进行了恒定轴压卸除围压的试验，分析了岩石在卸荷条件下的变形和强度特性，回归得到由卸荷导致岩石破坏的强度经验准则。尤明庆等[3]介绍了模拟地下岩体破坏的三轴卸围压试验，以塑性变形量和本征强度统一研究了三轴压缩和卸围压两种力学过程，提出了材料参数弱化模量来描述岩样的本征强度降低，讨论了循环加卸围压过程。汪斌等[4]对锦屏大理岩开展了单轴加、卸载以及三轴压缩和高应力条件下的峰前、峰后卸围压等 4 种不同应力路径力学试验，得到了大理岩的应力-应变全过程曲线、变形破坏特征和主要力学参数的变化规律，揭示了锦屏大理岩加、卸载应力路径下力学特性差异。李宏哲等[5]开展大理岩加卸荷变形特性试验，从描述岩石体积变形规律的角度出发，在对Weng模型改进的基础上建立了锦屏大理岩加、卸荷本构模型。刘建等[6]对砂岩开展若干围压的保持轴压不变峰前卸围压试验，研究了砂岩卸荷过程中的变形特征、破坏形态、峰值强度与残余强度特性及其扩容参数演化特征。黄润秋等[7]试验研究了高地应力条件下卸荷速率对锦屏大理岩力学特性的影响。周小平等[8]根据损伤断裂力学知识，建立了岩石处于卸荷条件下的全过程应力-应变关系，包括线弹性阶段、非线性强化阶段、应力跌落和应变软化阶段。李新平等[9]针对高地应力环境中的大理岩开展常规三轴压缩试验及峰前、峰后卸围压试验，通过试验数据对比分析，研究了大理岩的强度变形特征及破裂机制，吴刚等[10]也做了类似研究。周小平等[11]对卸荷岩体本构理论及其应用进行了较全面的总结。

对于岩石卸荷力学特性的试验研究取得了较大的进展，本文基于大理岩试件在不同围压（20、40、60 MPa）的峰前卸荷试验，建立了峰前卸荷条件下岩石的幂函数型Mohr强度准则，给出了数值仿真分析研究的大理岩峰前卸载条件，利用有限差分程序FLAC3D建立了数值仿真模型，对模型进行计算与分析，最后与室内试验结果果相对比，得到了峰前卸荷状态下大理岩力学特性的相关规律，为深部地下工程的开挖及安全防护提供了一定的理论依据。

2 试验方案

2.1 试验条件

试验所用岩样为锦屏二级水电站所取的大理岩，埋深2.1 km左右，试样试验前被加工成直径为50 mm，高度为100 mm的圆柱体，试件精度满足岩石力学试验的标准，新鲜岩石的表观密度为2.65～2.85 g/cm3，平均密度为2.70 g/cm3，吸水率为0.16%～0.25%。

本次试验采用的试验仪器为山东科技大学矿山灾害预防实验室的MTS815.03岩石三轴试验系统，在整个试验过程中，试验数据由MTS机自动采集，并转换为对应的应力应变信息输出到试验机的数据采集系统，并绘出相应的应力-应变曲线。

2.2 试验方案

为系统地研究大理岩峰前卸荷应力路径下的变形、参数及强度特性，试验的卸载应力路径采用恒轴压，卸围压的方式如图1所示。

图1 大理岩峰前卸荷试验应力路径Fig.1 Stress path of marble under pre-peak unloading test

大理岩峰前恒轴压卸围压试验分3个阶段：①施加一定的固定预加载使得试验试件固定后，采用静水压力条件（保持围压和轴向压力始终相等）以恒定的速率施加各向应力到预定的压力值（20、40、60 MPa）；②保持围压稳定的同时，以恒定的速率在轴线方向对岩石试件进行加载，直到轴向压力值达到岩石破坏前的某一状态（临界卸荷点)；③在保持轴向应力不变的前提下逐渐卸除围压直到岩样发生破坏。

峰前卸荷试验共选用 9 个试件，编号为A-1～A-9。本次峰前卸荷试验卸荷起始点取为三轴峰值强度的75%，试件试验方案及卸荷起始点见表1。

表1 峰前卸荷试验方案及试件编号Table 1 Scheme under pre-peak unloading test and numbers of specimens

3 大理岩峰前卸荷本构模型的建立

3.1 常用非线性强度准则

Mohr把库仑准则推广到考虑三向应力状态后得到：岩石在极限状态时，滑动面上的剪应力达到一个由剪切面上的正应力和岩石材料性质共同决定的最大值；剪切强度与剪切面上正应力的函数形式有多种，在几何形式上是一系列极限Mohr圆的包络线，它由试验数据拟合获得，滑动面上的剪切强度τ与该面上法向应力的函数即τ=f （σ）。

目前已提出的的非线性 Mohr强度包络线形式主要有双曲线型、二次抛物型以及幂函数型等。抛物线型、幂函数型、双曲线型Mohr强度准则都能较好地解决传统线性Mohr强度理论的一些不足，但双曲线型Mohr强度准则存在一定的局限性。双曲线的几何性质之一是有渐进线，当围压较大时，剪应力和正应力的关系曲线会呈现出近似线型变化，因此认为幂函数型和抛物线型Mohr强度准则在解释峰前卸荷试验的强度准则方面更为合理。

二次抛物线型和幂函数型摩尔强度准则的表达式为

二次抛物线型Mohr 强度准则：

幂函数型Mohr强度准则：

式中：σt为单轴抗拉强度；a、b分别为与材料特性有关的参数，通过拟合试验数据获得。

3.2 岩石非线性强度特性

提取Mohr应力圆的包络线与摩尔圆的所有切点数据，分别采用式1、2对切点数据进行拟合，拟合过程采用origin数值软件完成。拟合的数值结果见表3，图形结果如图3所示。

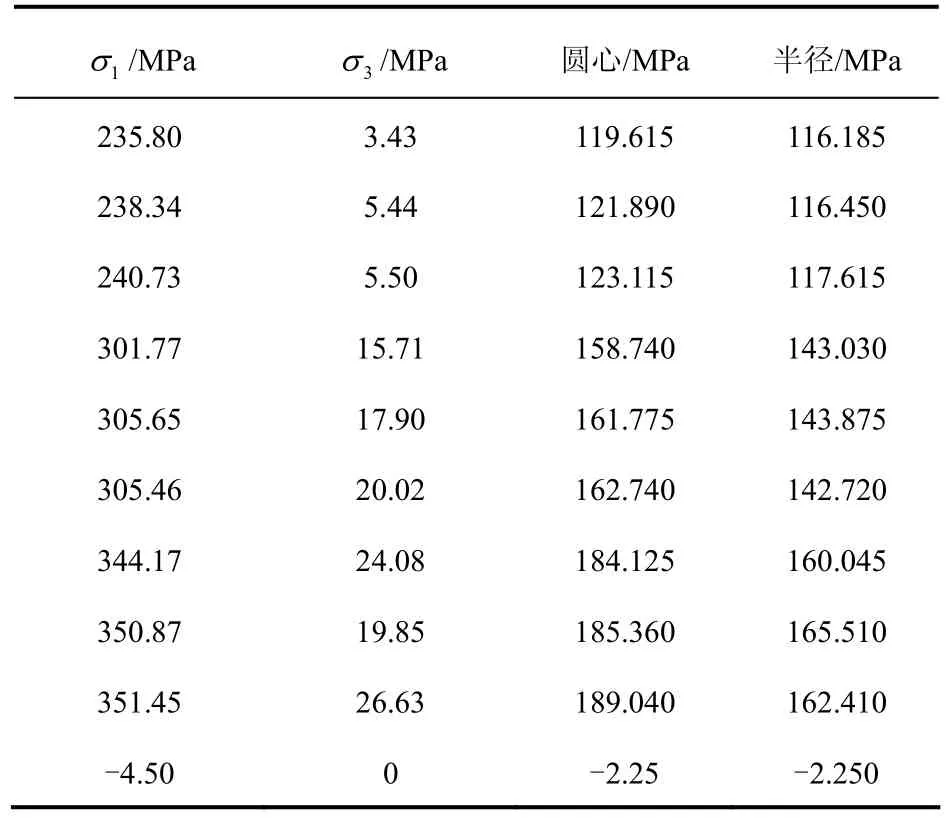
表2 峰前卸荷试验破坏状态Table 2 Damage states under pre-peak unloading tests

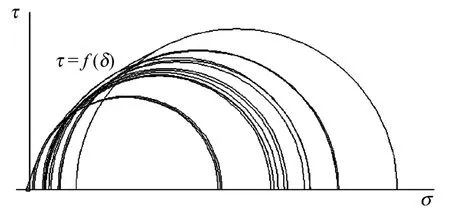
图2 大理岩峰前卸荷试验应力路径Fig.2 Stress path of marble under pre-peak unloading test

表3 非线性强度准则拟合结果Table 3 Fitting results in nonlinear strength criterion

图3 峰前卸荷试验非线性强度准则拟合结果Fig.3 Fitting results in nonlinear strength criterion under pre-peak unloading test

由表3及图3可见，二次抛物线型和幂函数型强度准则均能较好的反映高应力条件下峰前卸荷岩石的非线性力学特性，两者的相关系数接近，稳定性均较好；通过二次抛物线型Mohr 强度准则计算得到的单轴抗拉强度不符合试验抗拉强度，而通过幂函数型Mohr 强度准则计算得出的单轴抗拉强度与试验结果较为接近，因此选择幂函数型Mohr 强度准则作为峰前卸荷力学特性的非线性强度则。

幂函数型Mohr 强度准则能够合理地描述高应力条件下峰前卸荷岩石的非线性力学特性，相较于其他形式的非线性Mohr强度准则，幂函数型强度准则可以比较广泛的反映岩石的非线性强度特性。

4 数值仿真试验

4.1 计算模型及方案

根据室内试验模型的特点，采用有限差分程序FLAC3D软件建立了三维空间范围内的数值计算模型，圆柱体模型尺寸为直径为50 mm、高100 mm。计算模型的y轴方向为重力方向，x、z轴为围压施加方向，网格划分为 40×80×40个四边形单元。模型简图及网格划分图如图4所示。

图4 计算模型及网格划分图Fig.4 Computational model and meshing generation

边界条件：模型底面施加y方向的位移约束，上表面施加轴向压应力σ1，侧向施加围压σ2应力。

4.2 计算方案

利用有限差分程序FLAC3D建立了数值仿真模型，对模型进行计算与分析，峰前卸荷试验中幂函数型Mohr强度准则通过fish语言求解不同应力状态时对应的强度参数得以实现。仿真试验按以下两个步骤进行：①在初始围压(10、20、30、40、50、60 MPa)保持不变的情况下，以恒定的速率增加轴压直至其达到预定的卸荷点。②在轴向压力保持恒定的条件下，以恒定速率(0.05、0.1、0.5 MPa/s)卸除围压直至岩石发生破坏。

数值仿真试验中所采用的材料参数均来源于室内试验，对于黏聚力c值、内摩擦角φ值的计算，在峰前卸围压试验中采用Mohr-Coulomb强度包络线法，在常规三轴压缩试验中采用莫尔-库伦强度包络线法和σ1-σ3曲线法的平均值，见表4。

4.3 峰前卸荷室内、数值试验对比分析

图5为岩样在相同卸荷速率(0.05 MPa/s)、不同围压(20、40、60 MPa)条件下峰前卸荷室内、数值试验的应力-应变关系曲线对比图。

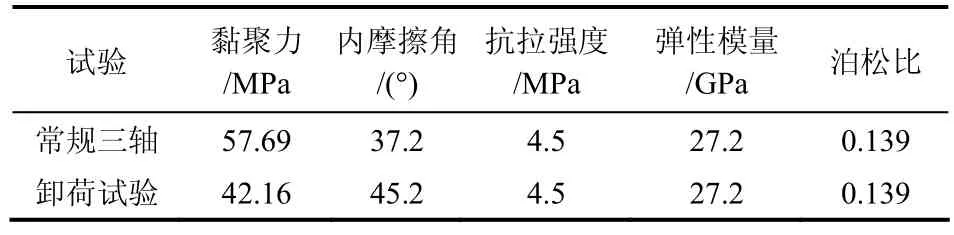
表4 数值试验的材料参数Table 4 Material parameters of simulation test

图5 大理岩峰前卸荷室内、数值试验应力-应变关系曲线Fig.5 The stress-strain relationship curves of marble under pre-peak unloading tests and numerical simulations

分析数值试验(在卸围压过程中当差应力发生应力降时即停止计算)与室内试验所得到的应力-应变关系曲线对比图可见，（1）数值仿真试验的峰前卸荷轴向应力-应变曲线与室内试验所得的峰前卸荷轴向应力-应变曲线符合的较好；（2）在保持围压为(20、40、60 MPa)恒定，以一定的加载速率增加轴压到达卸荷点的过程中，岩石试件未达到屈服应力，岩样的变形主要为弹性变形，轴向应力-应变曲线呈现出近似线性关系。通过对比发现，两者的初始值和终值基本符合，说明了数值试验在大理岩峰前卸荷试验加载阶段的合理性；（3）在保持轴压恒定、以恒定的速率（0.05 MPa/s）卸除围压直至岩石发生破坏的过程中，初始阶段轴向应变基本保持不变，在卸围压进行到一定程度时，轴向应变才开始增长，从图形上看轴向应力-应变曲线逐渐趋于水平。岩石试件在差应力变化很小时，轴向应变增长较快，表现出较为明显的塑性变形特征。产生这一现象的主要原因是：在峰前卸围压试验中开始卸除围压时，轴向压力没有达到峰值强度，大理岩试件没有达到屈服应力，因而轴向变形没有立即进入到塑性变形阶段，此阶段中轴向应力-应变关系曲线近似呈现出较理想的弹塑性模型。

4.4 围压影响

图6为卸荷速率为0.05 MPa/s不同围压时大理岩峰前卸荷数值试验的轴向应力-应变关系曲线。从图中可以看出，随着围压增大，岩石试件发生卸荷破坏时的峰值强度逐渐增大，发生破坏时围压降值也不断增大。这是由于随着围压的增加，岩石试件的孔隙得到了进一步的压密，岩石材料的质量提高，同时也限制了岩石内部裂隙的产生和扩展，因而在岩石试件发生卸荷破坏时的峰值强度随着围压的增长而变大。

图6 不同围压下峰前卸荷数值试验应力-应变关系曲线Fig.6 The stress-strain relationship curves under pre-peak unloading of numerical simulation under different confining pressures

大理岩峰前卸围压试验的卸荷点发生在轴向压力未达到岩石峰值强度之前，在卸荷发生时，岩石试件并没有立即进入到塑性变形阶段，应变关系呈现出较理想的弹塑性模型。

4.5 卸荷速率作用

图7为不同围压不同卸荷速率时大理岩峰前卸荷数值试验应力-应变关系曲线。表 5为大理岩在卸荷破坏时的轴向应变及围压降值。

图7 不同卸荷速率下峰前卸荷数值试验应力-应变关系曲线Fig.7 The stress-strain relationship curves under pre-peak unloading of numerical simulation at different unloading velocities

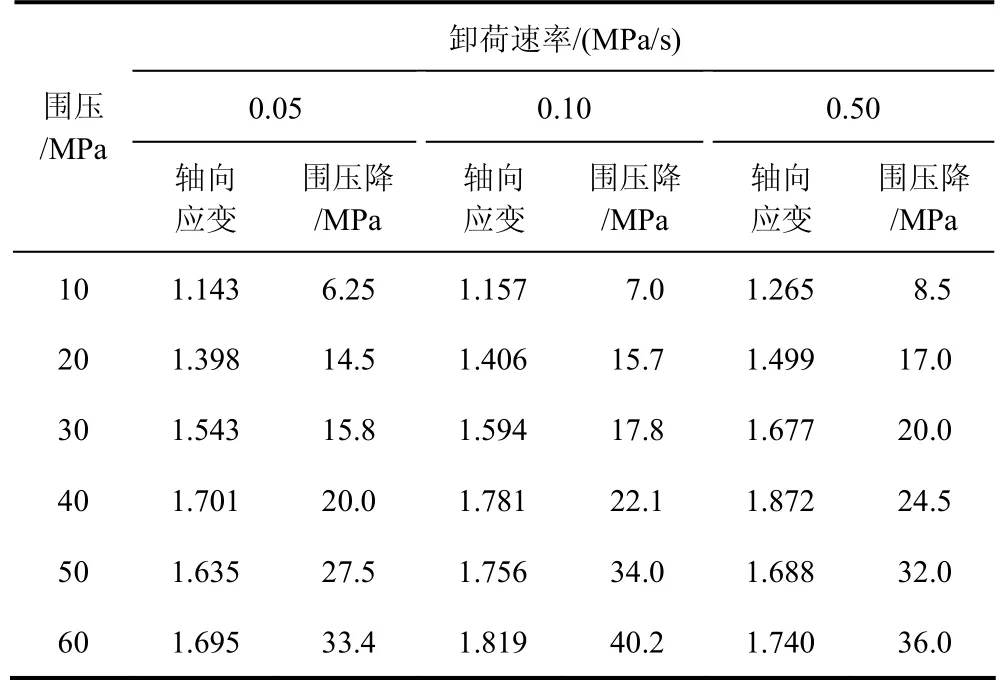
表5 大理岩卸荷破坏时轴向应变及围压降值Table 5 Axial strain and reducing of confining pressure when the marble is failure under unloading conditions

结合图7、表5可见，当围压处于10～40 MPa之间时，卸荷速率越大，卸荷过程中岩石试件发生破坏时所产生的围压降值越大。这是由于在此围压区间内，当卸荷速率过快时，岩石试件没有足够的时间发生彻底的变形破坏，仍具有承载能力，当围压值处于10～40 MPa之间时，卸荷速率越大，峰前卸荷试验过程中岩石试件发生卸荷破坏时所产生的围压降值越大；当围压大于50 MPa的条件下，当卸荷速率为0.1 MPa/s时，岩石试在卸荷过程中发生破坏时所产生的围压降值最大，卸荷速率与围压降值没有体现出明显的规律。

5 结 论

（1）将目前已有的非线性 Mohr强度准则结合试验数据，对比分析了二次抛物线型和幂函数型强度准则，建立了可较好地描述高应力条件下峰前卸荷岩石的非线性力学特性的幂函数型Mohr 强度准则。

（2）在峰前卸荷试验中，开始卸除围压时，轴向压力没有达到峰值强度，轴向应力-应变关系曲线近似呈现出较理想的弹塑性模型。

（3）随着围压增大，岩石试件发生破坏时的峰值强度和围压降值逐渐增大。

（4）围压处于10～40 MPa之间时，卸荷速率越大，卸荷过程中岩石试件发生破坏时所产生的围压降值越大；在围压大于50 MPa时，没有明显的规律性。

[1] SWANSON S R.An observation of loading path independence of fraeture rock[M].Int.J.Rock Mech.Min.Sci., 1971, 8(3): 277－281.

[2] 陶履彬, 夏才初, 陆益鸣.三峡工程花岗岩卸荷全过程特性的试验研究[J].同济大学学报, 1998, 26(3): 330－334.TAO LV-bin, XIA Cai-chu, LU Yi-ming.Experimental studies on the total course behavior of unloading of granite in Three Gorges Project of the Yangtze River[J].Journal of Tongji University, 1998, 26(3): 330－334.

[3] 尤明庆, 华安增.岩石岩样的三轴卸围压试验[J].岩石力学与工程学报, 1998, 17(1): 24－29.YOU Ming-qing, HUA An-zeng.Triaxial confining depressure test of rock sample[J].Chinese Journal of Rock Mechanics and Engineering, 1998, 17(1): 24－29.

[4] 汪斌, 朱杰兵, 邬爱清, 等.锦屏大理岩加、卸载应力路径下力学性质试验研究[J].岩石力学与工程学报,2008, 27(10): 2138－2145.WANG Bin, ZHU Jie-bing, WU Ai-qing, et al.Experimental study on mechanical properties of Jinping marble under loading and unloading stress paths[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(10): 2138-2145.

[5] 李宏哲, 夏才初, 肖维民.锦屏水电站大理岩加、卸荷本构模型研究[J].岩石力学与工程学报, 2010, 29(7):1489-1495.LI Hong-zhe, XIA Cai-chu, XIAO Wei-min.Research on constitutive model of marble of Jinping Hydropower Station under loading and unloading conditions[J].Chinese Journal of Rock Mechanics and Engineering,2010, 29(7): 1489－1495.

[6] 刘建, 李建朋.砂岩高应力峰前卸围压试验研究[J].岩石力学与工程学报, 2011, 30(3): 473－479.LIU Jian, LI Jian-peng.Experimental research on sandstone pre-peak unloading process under high confining pressure[J].Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 473－479.

[7] 黄润秋, 黄达.高地应力条件下卸荷速率对锦屏大理岩力学特性影响规律试验研究[J].岩石力学与工程学报, 2010, 29(1): 21－33.HUANG Run-qiu, HUANG Da.Experimental research on effect laws of unloading rates on mechanical properties of Jinping marble under high geostress[J].Chinese Journal of Rock Mechanics and Engineering,2010, 29(1): 21－33.

[8] 周小平, 哈秋舲, 张永兴, 等.峰前围压卸荷条件下岩石的应力-应变全过程分析和变形局部化研究[J].岩石力学与工程学报, 2005, 24(18): 3237－3244.ZHOU Xiao-ping, HA Qiu-lin, ZHANG Yong-xing.Analysis of localization of deformation and complete stress-strain relation for mesoscopic heterogenous brittle rock materials when axial stress is held constant while lateral confinement is reduced[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3237－3244.

[9] 李新平, 肖桃李, 汪斌, 等.锦屏二级水电站大理岩不同应力路径下加卸载试验研究[J].岩石力学与工程学报, 2012, 31(5): 882－889.LI Xin-ping, XIAO Tao-li, WANG Bin, et al.Experimental study of Jinping Ⅱ hydropower station marble under loading and unloading stress paths[J].Chinese Journal of Rock Mechanics and Engineering,2012, 31(5): 882－889.

[10] 吴刚, 孙钧, 吴中如.复杂应力状态下完整岩体卸荷破坏的损伤力学分析[J].河海大学学报, 1997, 25(3): 44－49.WU Gang, SUN Jun, WU Zhong-ru.Damage mechanical analysis of unloading failure of intact rockmass under complex stress state[J].Journal of Hehai University,1997, 25(3): 44－49.

[11] 周小平, 张永兴.卸荷岩体本构理论及其应用[M].北京: 科学出版社, 2007.