一般SPT模型的抗差分和线性攻击安全性研究

刘凤梅，陈连俊，李春祥，李艳梅，张国双

（信息保障技术重点实验室，北京 100072）

1 引言

差分攻击和线性攻击是对分组密码最有效的2种攻击方法，研究和评估密码算法抵抗差分攻击和线性攻击的能力，是密码设计者和分析者必须考虑的问题[1~3]。SPS模型（如图1和图2所示）是分组密码的一个基本模型[3~5]，它主要是由混淆层－扩散层－混淆层组成，通常会在第2层混淆之前异或加入轮密钥。对于分组密码来讲，为了保证其能够解密，一般要求每个iS（1in≤≤）都是置换且上下2个混淆层是完全一样的。

近年来，在序列密码的设计中，人们也广泛应用将混淆和扩散分层实现的设计理念[6~8]。与分组密码不同的是，对于序列密码，在采用SP网络时，由于其解密机制不同于分组密码，且可以使用压缩环节来实现输入多输出少的功能，因此在“混淆层－扩散层－混淆层”这一设计模型中，上下2个混淆层可以不一样，也不需要其中S盒都是置换。具体来说，序列密码中利用分组密码的迭代思想时既可以先迭代最后再压缩[6]，也可以边迭代边压缩[7]。因此，在序列密码的设计中，为同时且高效地实现迭代和压缩（多输入少输出），可以使用更加一般的SPT模型（如图3和图4所示），这里S和T表示2个不同的混淆层，而且每个S或T都不必是置换。这就需要对SPT模型抗已知攻击的能力进行评估，弄清一般SPT模型抵抗差分攻击和抵抗线性攻击的能力。

对于SPS模型的抗差分攻击和抗线性攻击的安全性问题，一直是受到密码学者关注，也已有了完善的结果[9~13]。但对于更一般的可实现压缩功能的SPT模型的抗差分攻击能力和抗线性攻击能力却未见研究。本文正是在这一背景需求下进行研究的，通过分析，本文克服了S变换和T变换的非双射性给证明过程带来的困难，给出了一般SPT模型在P为最佳扩散层时抗差分攻击和线性攻击（S变换和T变换平衡时）能力估计的结果，这对于该模型在序列密码设计中的应用有重要的意义。

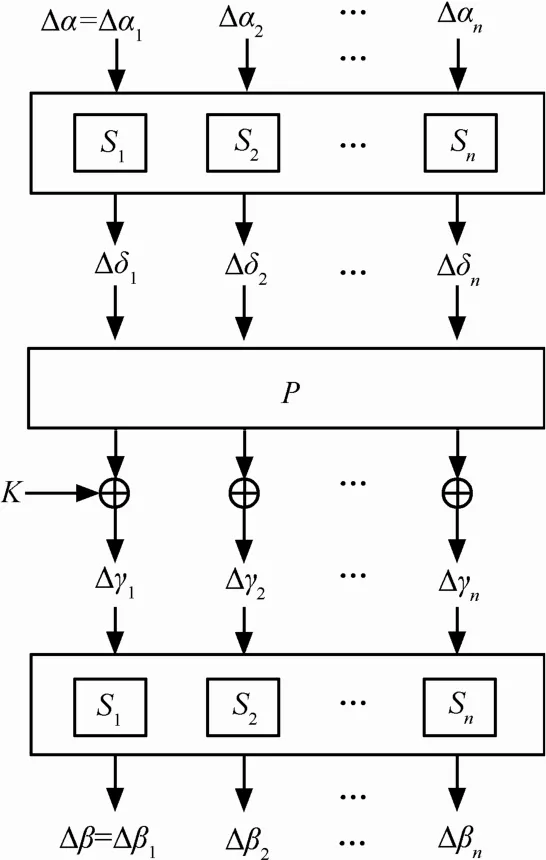
图1 SPS模型(差分路径)

图2 SPS模型(线性路径)

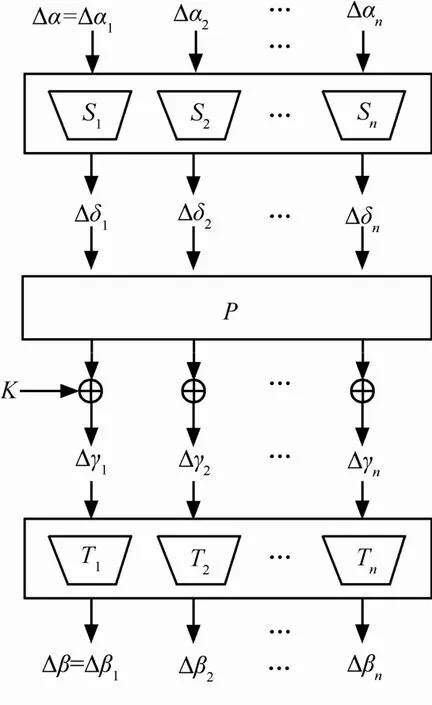
图3 SPT模型(差分路径)

本文第2节给出了相关定义和已有的结论；在第3节中，研究了如图3所示的一般SPT模型在P为最佳扩散层时抗差分攻击的安全性问题，给出了该模型的最大差分概率上界。

在第4节中，研究了如图4所示的一般SPT模型在P为最佳扩散层且S变换及T变换平衡时抗线性攻击的安全性问题，给出了类似于SPS模型的最大线性逼近优势的上界和最大线性包优势的上界。

2 相关定义和已有结论

图3和图4中各记号约定如下。

设m,m1,m',n为4个正整数，且 m ≥ m ' ≥m1。i = 1 ,… ,n 。

记 Δα = (Δ α1, Δ α2, … ,Δ αn)， Δ β = (Δ β1,Δβ2,… ,Δ βn)，Δδ = (Δ δ1,Δ δ2,…,Δ δn)，Δ γ = (Δγ1,Δγ2, … ,Δ γn)，其中，Δαi∈ G F(2)m，Δ βi∈ G F(2)m1，Δδi,Δγi∈ G F(2)m'， i = 1,… ,n 。

记 Γα= ( Γ α1, Γ α2,… ,Γαn) ， Γ β=(Γ β1,Γβ2,… ,Γ βn)，Γδ = ( Γ δ1, Γ δ2,… ,Γδn) ，Γ γ=(Γ γ1,Γγ2,… , Γγn) ，其中，Γ αi∈ G F(2)m，Γ βi∈ G F(2)m1，Γδi∈ G F(2)m'， Γ γi∈ G F(2)m'， i = 1 ,… ,n 。

以wt(Δα)表 示 Δα 的 包 重 量 ， 即wt( Δ α ) = # ｛ i | Δ αi≠ 0 ｝;w t(Γ α)表示 Γα的包重量；以 MT表示矩阵M的转置。

P:(GF(2)m')n→(GF(2)m')n为线性变换，且其为最佳扩散层。

很容易有引理1~引理4。

引理1 设Δαi和Δδi分别为映射Si的输入差和输出差，则有 Δ αi=0⇒ Δ δi= 0 ；又若 Si是双射，则 Δ αi≠ 0 ⇔ Δδi≠0。

引理2 设Δδ和Δγ分别为P的输入差和输出差，且P的分支数为n+1，则有wt(Δδ)+wt(Δγ)≥ n +1。

引理5[10]设n×n矩阵M对应于变换P，则P的分支数为 n +1，当且仅当对于任意1 ≤ k ≤ n ，M的k×k子矩阵的秩为k（此时，MT的k×k子矩阵的秩也为k）。

引理6[10]设图 1中 Si(i = 1 ,… ,n )均为置换且型SPS的最大差分概率上界为ρn。GF(2)m， Γ y ∈ G F(2)m'，S的线性优势[9]定义为

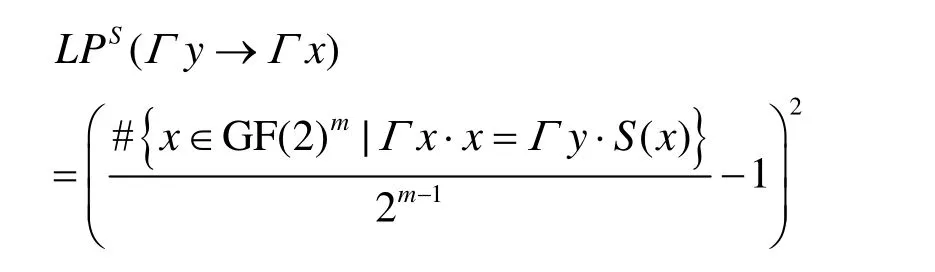
其中，Γx⋅x表示Γx和x的点积。S的最大线性优势定义为

根据Walsh谱[14]的定义，有

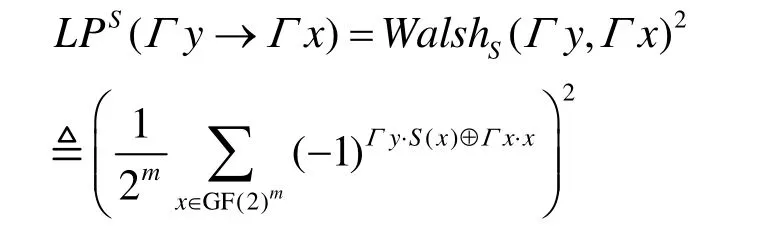
通常考察图4所示模型SPT的2种线性优势。

定义 3 (SPT的线性逼近优势)[9]设Γα∈GF(2)m,Γδ, Γ γ∈ G F(2)m',Γ β∈ G F(2)m1,SPT的线性逼近优势定义为

SPT的最大线性逼近优势定义为

定义4 （SPT的线性包优势）[9]设 Γ α∈G F(2)m,Γδ,Γ γ∈ G F(2)m',Γ β∈ G F(2)m1,SPT的线性包优势定义为

SPT的最大线性包优势定义为

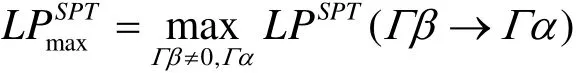
引理7[9]设图2中的 S ， i = 1 ,… ,n 均为置换，i衡当且仅当对任意 Γ y ∈GF(2)m'且Γy≠0，都有WalshS(Γ y,0) = 0。

由Walsh谱的定义及引理8有以下推论。

推论 1 设映射 S :GF(2)m→ G F(2)m'为平衡的，Γ x ∈ G F(2)m，Γ y ∈ G F(2)m'，则S的线性优势有如下性质：

引理9[14]Parseval等式：

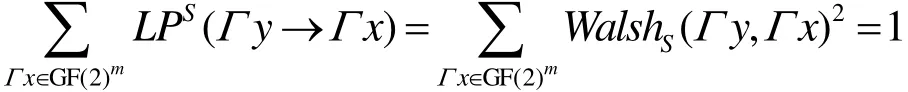
引理 10[10]设P对应于矩阵 M =(mij)n×n，

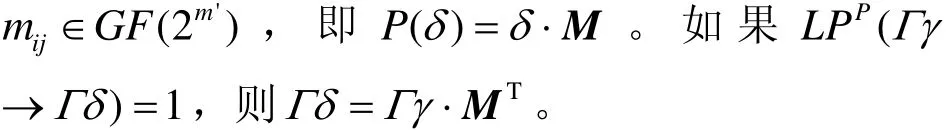
3 SPT模型的抗差分攻击性

引理11 设n×n矩阵M对应于变换P（即P(δ)=δ⋅M），且P是最佳扩散层，Δγ=Δδ⋅M。再设wt(Δδ)=j，{i1,…,ij}为Δδ的非零分位的序号构成的集合， s ≥ 1， w t( Δ γ) = n - s +1且 Δγ1=…决定。

证明 若 s =1，结论显然成立。设 s ＞ 1。取M的子矩阵，记Δδ'=(Δ δi1,… ,Δ δij)，则由题设知 Δδ⋅M的第1～s-1列=Δδ'⋅M'， 再 由 Δγ=Δδ⋅M知Δδ' ⋅ M ' =(Δ γ1,… ,Δ γs-1) = 0。

记

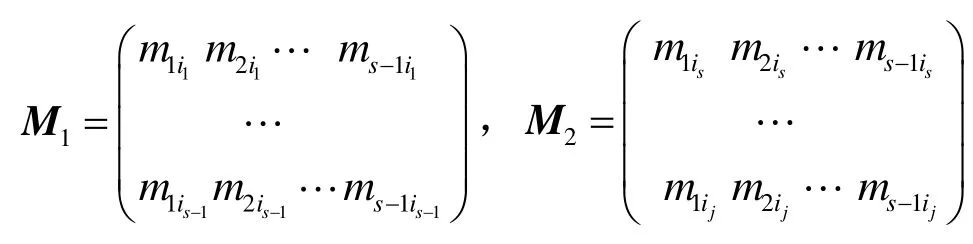
则由P的分支数是 n +1和引理5知， M1可逆，且Δδis,… ,Δδij决定。#

下面将借助引理11，克服由 Si和 Ti的非双射性引发的非零输入差可能产生零输出差的特性给研究过程造成的困难，获得下述结论。

定理1 设图3中P为最佳扩散层，记ρd=非零时的最大差分概率上界为 ρdn。

证明 本证明所用符号如图 3所示。设wt(Δ α)=k， Δβ≠0，且wt( Δ β )= n - s +1，不失一般性，不妨设 Δ α1≠0,… , Δαk≠0， Δ βi1≠0,…,

假设密钥K的各分位是相互独立且服从均匀分布的，则可认为SPT模型中各层输入的各路彼此是独立的，且Δα与Δγ独立，因而

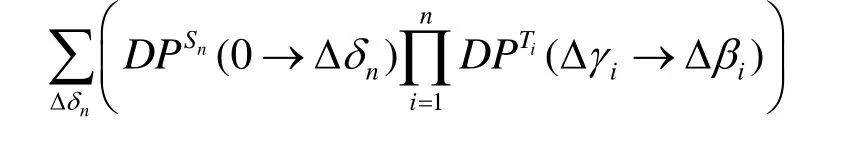
由引理4，有

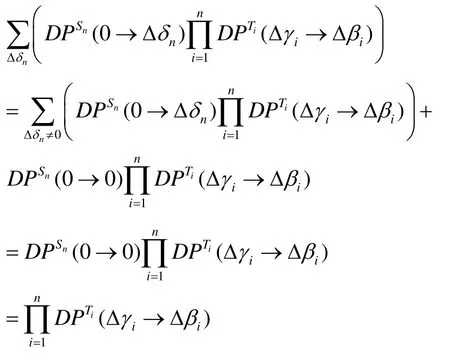
依此类推：

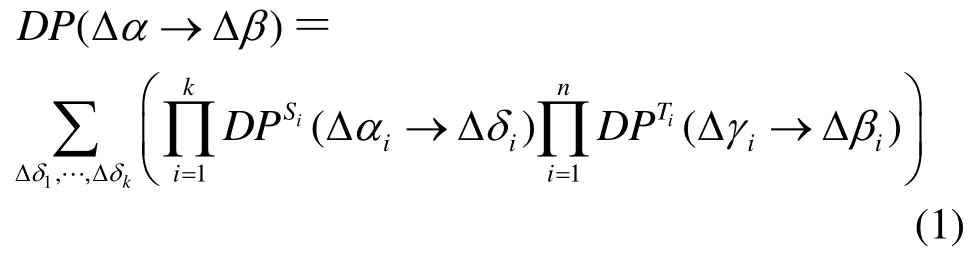
将所有可能的（即所有正概率差分路径上的）Δδ 所在集合记为Mδ，则式(1)中的求和实际上是对 Δ δ ∈ Mδ求和。Δδ ∈ Mδ,wt(Δ δ)=k1，且对于Δγ=Δδ⋅M,wt(Δγ)= n - s1+ 1 }，记所有可能的(k1,s1)所在的集合为Γ。则为诸 Mk1,s1的不交并。注意Δδ≠0（否则Δβ=0）且任意Δδ的非零位一定包含于{1,…,k},故1 ≤ k1≤ k 。又由 P的分支数为n+ 1 和引理2可知 k1≥s1≥1。故式(1)求和可化为

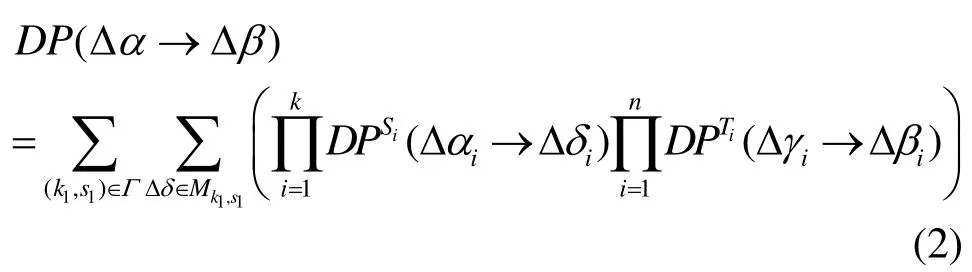
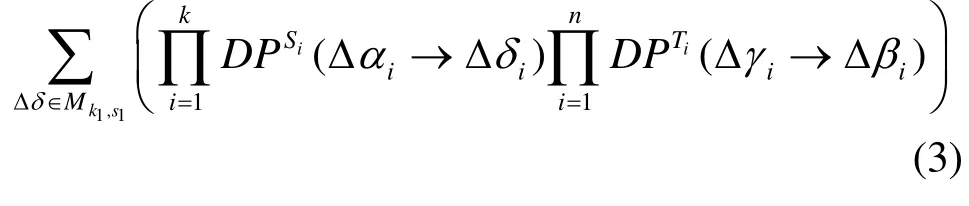
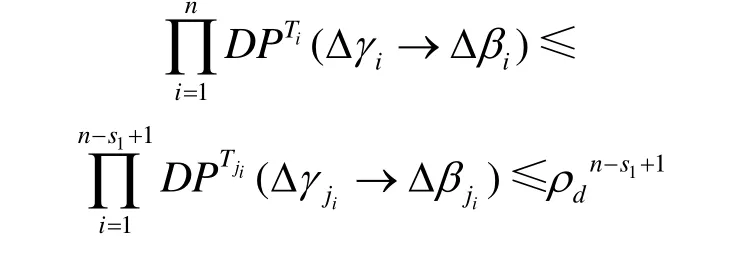
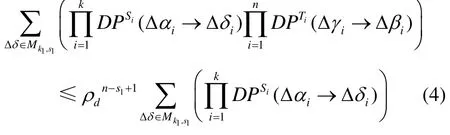
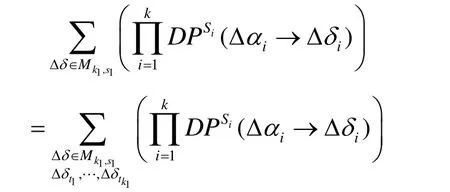
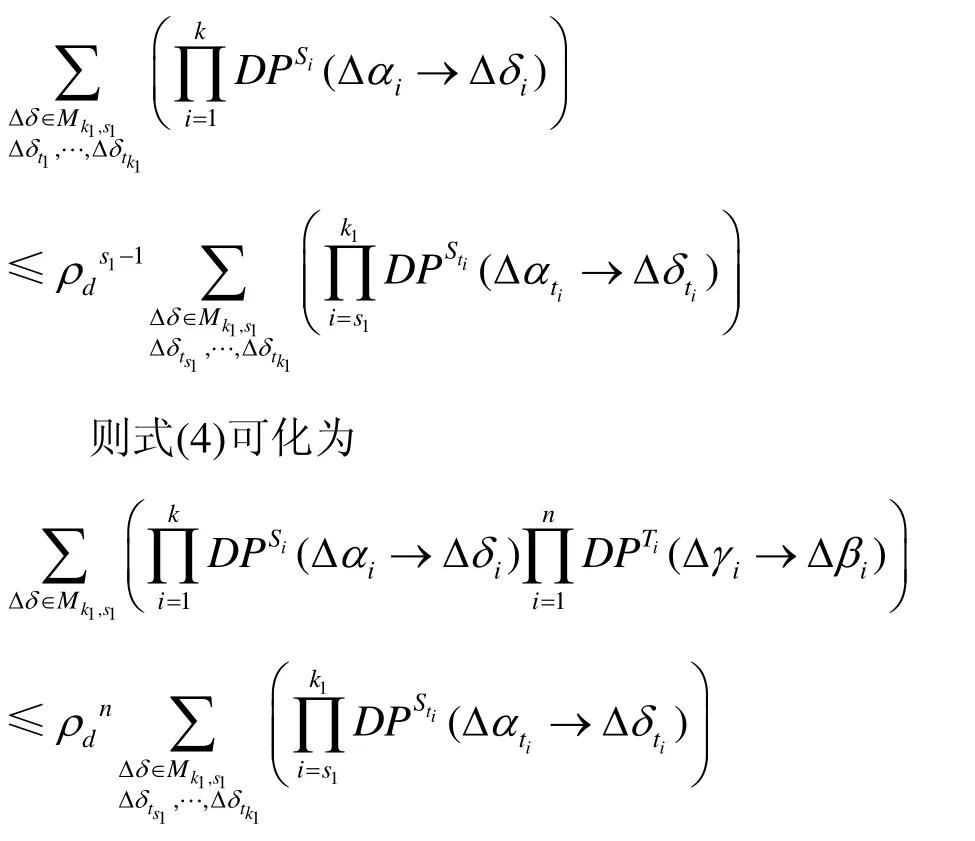
此即为式(3)的估计，进而由式(2)可知：

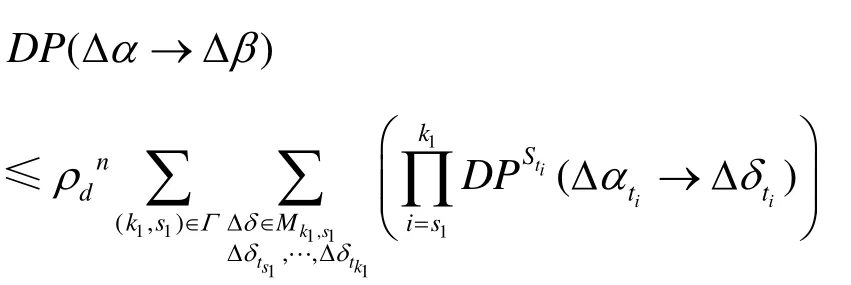
因此图 3所示模型SPT的输出差非零时的最大差分概率上界为 ρdn。

定理2 设图3所示模型SPT中P为最佳扩散层，其输入差为Δα且wt(Δα)=k，记

证明 同定理1证明，将所有可能的Δδ所在集合记为Mδ，则Mδ中可能含有0（S为压缩变换时），同样的推理可以得到

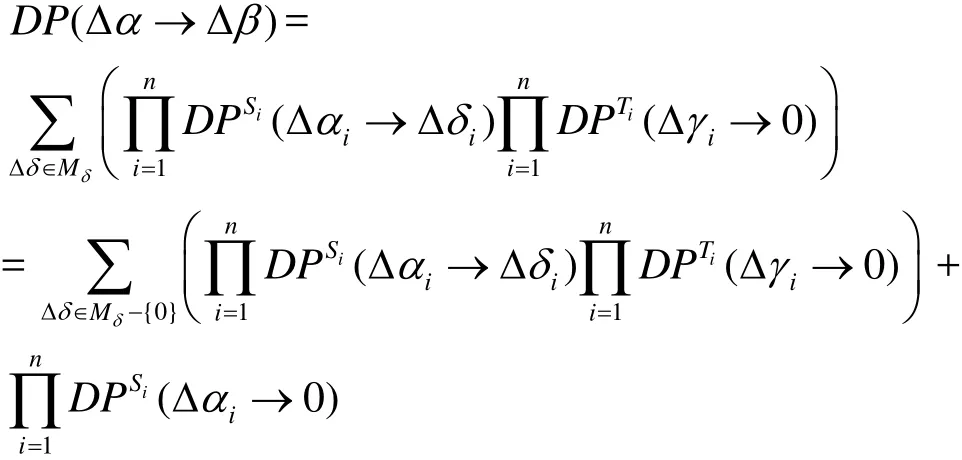
类似于定理1可证

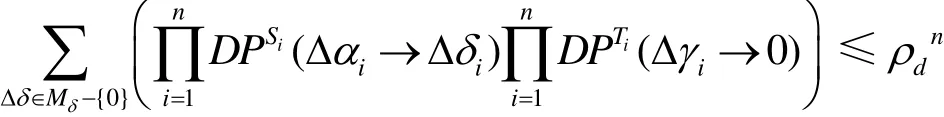
4 SPT模型的抗线性攻击性

定理 3 设图 4中 P为最佳扩散层且 Si,Ti,则图 4所示模型SPT的最大线性逼近优势

证明 设 w t(Γ β) = k≥1，Γβ1≠ 0 ,… ,Γ βk≠0，Γα≠ 0 ，且设 Γ αis≠ 0 ,… , Γαin≠ 0 ， Γ αi1= 0 ,…,

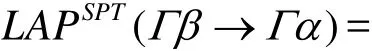
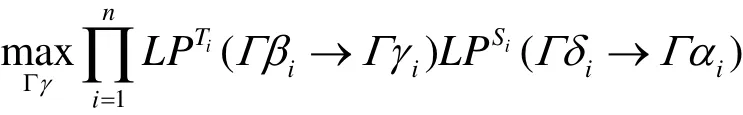
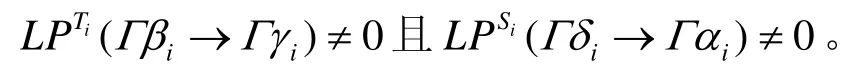
已知 Γ β1≠ 0 ,… ,Γ βk≠0， Γ βk+1=0,…,Γ βn=0，虑到 Ti、 Si平衡，由推论1有， Γ γ1≠ 0 ,… ,Γ γk≠0且 Γγk+1= 0,… ,Γ γn=0； Γ δis≠ 0 ,… , Γδin≠ 0 ，

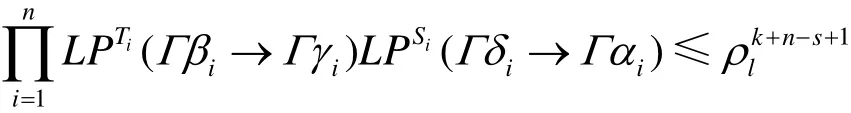
又由变换P的分支数为 n +1，故 k + n - s +1

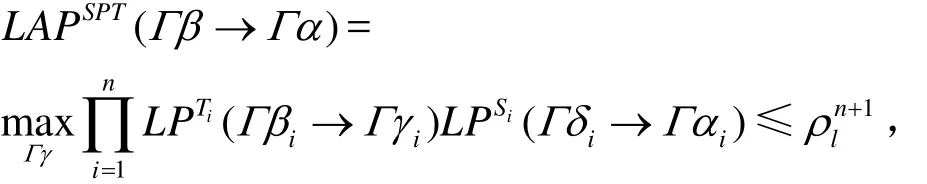
引理 12 设矩阵 M 对应于变换P，Γδ=Γγ⋅MT， w t( Γ δ) = n -s +1，wt(Γγ)=k（则= Γ δs-1= 0 ，则存在指标集 { i1, …,is-1}使得Γγi1≠

证明 结合引理5和引理10，对矩阵 MT利用类似于引理11的证明方法即可得证。#

定理4 设图4中 Si, Ti,i = 1 ,… ,n 均为平衡函数

证明 设 w t(Γ β) = k≥1，Γβ1≠ 0 ,… ,Γ βk≠0，Γβk+1= 0 ,… ,Γ βn=0， w t( Γ α) = n - s + 1， s ≥ 1，Γαis≠ 0 ,… , Γαin≠ 0 ， Γ αi1= 0 ,… , Γαis-1= 0 。同定理3在题设条件下，只需考察Γα≠0时的情形。

由线性包优势的定义：

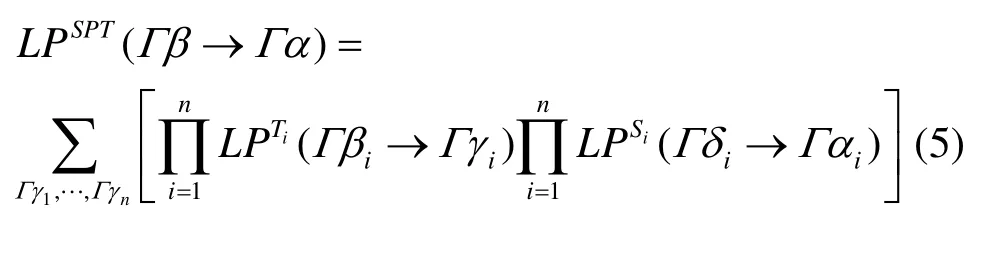
已知 Γ β1≠0,…,Γ βk≠0，Γβk+1= 0 ,… , Γ βn= 0 ，考虑到 Ti平衡，由推论1，若则 Γ γ1≠ 0 ,… ,Γ γk≠0且 Γ γk+1= 0 ,… , Γγn= 0 。再注意 L PTi(0 → 0 )= 1，故式(5)可化为

又 已 知 Γ αis≠ 0,… , Γαin≠ 0 , Γ αi1= 0 ,… ,，考虑到 Si平衡，同样若≠ 0 ，则 Γ δis≠ 0 ,…, Γ δin≠ 0 ,Γ δi1= 0 ,… , Γ δis-1= 0 。

因此对于给定的Γγ，且Γγ的非零位为{1,… ,k }，

由以上分析，若记：

则式(6)可化为

因此只需考察Γ中的Γγ。对于Γγ∈Γ，由引理12可知，存在指标集{ js, … , jk} ⊆ {1,… ,k }，使得Γγ1,… ,Γγk由Γγjs,…,Γγjk决定。因此由式(7)得：

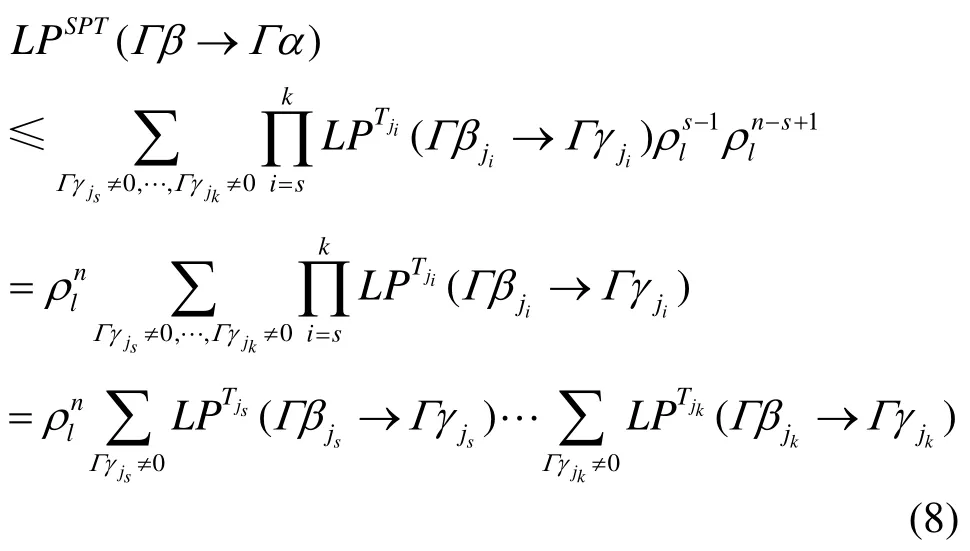
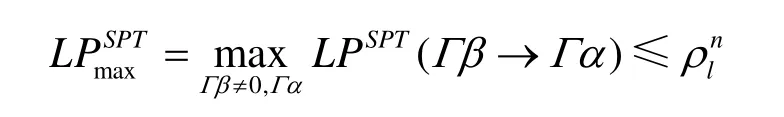
注：在对SPT模型最大线性逼近优势和最大线性包优势上界的估计中，其中所用S变换和T变换的平衡性是最关键的。

5 结束语

SPS网络是分组密码的一个基本模型，能够同时实现压缩功能的SPT模型是该模型的推广，在序列密码的设计中具有重要的应用价值。本文在P为最佳扩散层的条件下，研究了该模型的抗差分攻击的安全性和抗线性攻击（S和T平衡）的安全性，分别给出了其差分概率的上界、最大线性逼近优势的上界和最大线性包优势的上界，这些结论对于序列密码的设计和分析具有现实的意义。在今后的工作中，还将研究该模型在更宽松条件下的抗差分和线性攻击性能，并研究更加紧致的上界。

[1] KIM J S, LEE C H, SUNG J C, et al. Seven new block cipher structures with provable security against differential cryptanalysis[J].IEICE Trans Fundamentals, 2008,92(10): 3047-3058.

[2] SU B Z, WU W L, ZHANG W T. Security of the SMS4 block cipher against differential cryptanalysis[J]. Journal of Computer Science and Technology, 2011,26(1): 130-138.

[3] 张文涛, 卿斯汉, 吴文玲. 嵌套Feistel结构的SP型分组密码的可证明安全性[J]. 计算机研究与发展, 2004, 41(8): 1389-1397.ZHANG W T, QIN S H, WU W L. Provable security for SPN block cIphers containing feistel structure[J]. Journal of Computer Research and Development, 2004,41(8): 1389-1397.

[4] 魏悦川, 孙兵, 李超. FOX密码的不可能差分攻击[J]. 通信学报,2010, 31(9): 24-29.WEI Y C, SUN B, LI C. Impossible differential attacks on FOX[J].Journal on Communication, 2010, 31(9): 24-29.

[5] KELIHER L. Refined analysis of bounds related to linear and differential cryptanalysis for the AES[A]. AES 2004, LNCS 3373[C]. 2005. 42-57.

[6] BIRYUKOV A. Design of a new stream cipher-LEX, new stream cipher designs[A]. LNCS 4986[C]. 2008. 48-56.

[7] DAEMEN J, KITSOS P. The self-synchronizing stream cipher:MOUSTIQUE, new stream cipher designs[A]. LNCS 4986[C]. 2008.210-223.

[8] DE Cannière C，PRENAAL B, TRIVIUM. New stream cipher designs[A]. LNCS 4986[C]. 2008.244-266.

[9] KANG J S, HONG S, LEE S, et al. Practical and provable security against differential and linear cryptanalysis for the substitution- permutation networks[J]. ETRI Journal, 2001, 23(4):158-167.

[10] HONG S, LEE S, LIM J, et al. Provable security against differential and linear cryptanalysis for the SPN structure[A]. FSE 2000, LNCS 1978[C]. 2001. 273-283.

[11] 吕述望, 范修斌, 王昭顺等. 完全映射及其密码学应用[M]. 合肥:中国科学技术大学出版社, 2008.LV S W, FAN X B, WANG Z S, et al. Complete Mapping and Application in Cryptography[M]. Hefei: University of Science and Technology of China Press, 2008.

[12] 吴文玲, 冯登国, 张文涛. 分组密码的设计与分析（第2版）[M]. 北京: 清华大学出版社, 2009.WU W L, FENG D G, ZHANG W T, The Design and Analysis of Block Ciphers(Second Edition)[M]. Beijing: Tsinghua University Press, 2009.

[13] KELIHER L, MEIJER H, TAVARES S. New method for upper bounding the maximum average linear hull probability for SPNs[A].EUROCRYPT 2001, LNCS 2045[C]. 2001. 420-436.

[14] 金晨辉, 郑浩然, 张少武等. 密码学[M]. 北京: 高等教育出版社,2009.JIN C H, ZHENG H R, ZHANG S W, et al. Cryptology[M]. Beijing:Higher Education Press, 2009.