如何用EXCEL 进行附和导线近似平差的计算

杨 冲

(山西省勘察设计研究院，山西太原 030013)

0 引言

在煤矿测量工作中，经常进行单一附和导线的近似平差计算。传统的手工计算，不但效率低，而且算错之后不易改正(因为后一步的起算数据由前一步计算得到，一旦哪一步骤出错，后续步骤都需重新计算)。而在EXCEL界面上，可清晰、直观的显示计算的全部过程，加之其强大的函数计算功能，完全可以代替繁重的手工计算。

1 原理方法

1)计算角度闭合差 fβ，闭合差限差若 fβ＜ f容，则按角度个数平均分配fβ(将除不尽的1″分配到长边角度上)，获得各边转折角。

2)根据起始边(AB)的坐标方位角和改正后的转折角，推算其余各导线边的坐标方位角。

3)根据起始边(AB)的坐标、各边的坐标方位角、竖直角和边长，计算各点坐标增量，推求C点的坐标值(xd'，yd')。

4)计算C点坐标闭合差fs和导线全长相对闭合差，若不超限，则按距离分配fs。

5)计算各导线点平面坐标。

6)根据B点高程、各导线节长度和竖直角计算各点高差及终点C的高差闭合差fh，若不超限，按距离分配fh。

7)计算各导线点高程，见图1。

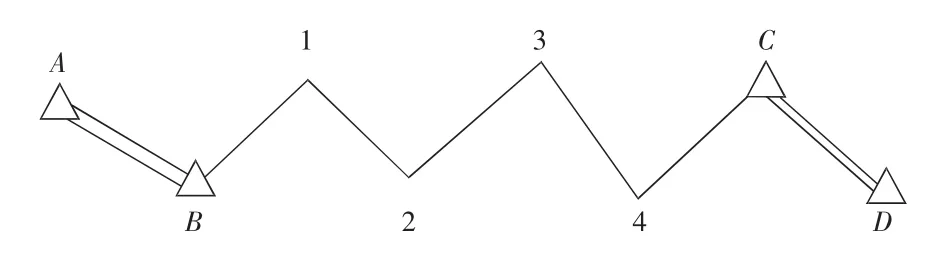
图1 各导线点位置图

2 问题处理

在计算过程中，我们会遇到一些问题。

首先是角度的运算问题。我们知道，在EXCEL中，不能对角度值直接进行三角函数运算，需要将角度值换算成弧度。这里有两个问题:

1)角度输入问题。

在EXCEL表格中，不能直接输入度、分、秒。这里，笔者提供一种输入角度的方法:首先自定义单元格格式，将其定义为［h］“°”mm“'”ss“″”的形式。角度值输入时，度、分、秒间以冒号隔开，例如“23:30:01”，输入完成后将自动显示为“23°30'01″”，这样输入的角度可直接进行加减运算;

2)角度的三角函数运算问题。

需运用角度转弧度函数“RADIANS()”。这里需要注意的是，先前输入的角度值需要乘以24，例如:COS(RADIANS(A1×24))(假设输入的角度值位置在A1上)。经过以上两个步骤，便可将斜距、水平角轻松转换为平距、坐标方位角。

再谈数值取位问题，我们知道，在角度计算中，遵循“四舍六入，五前奇进偶不进”原则。在坐标增量(Δx=S×cosα，Δy=S×sinα)计算时，我们也会遇到取位问题。如果一律按四舍五入方法计算，由于进位误差的累积，势必造成坐标增量偏大。故坐标计算时，也应遵循角度计算的取值方法，以避免因取值方法不当造成的误差累积。我们可以采用下面的方法实现这一过程。

需要用到EXCEL中的几个函数:取绝对值函数ABS、嵌套条件函数IF、取小数位数函数ROUND、取余数函数MOD。以中间计算过程保留四位小数为例。考虑到坐标增量存在正负号，故需先将要计算的数值取绝对值进行运算，最后再带上正负号。例如:ABS(A1)/A1。计算中需要检测小数点后第四位和第五位的数值(A1为要保留四位有效数字的数据)。

过程为:

1)如果 MOD(A1×10 000，1)＜0.5，则直接保留四位有效数字输出结果，即:ROUND(A1，4);

2)如果 MOD(A1×10 000，1)＜0.6，需要检测小数点后第四位(保留四位小数后)的数值，如果是偶数，则输出保留四位小数后的数值 ROUND(A1，4)，否则，输出 ROUND(A1，4)－0.000 1。

3)如果 MOD(A1 ×10 000，1)＞ =0.6，则输出 ROUND(A1，4)。具体实现算法为:

“=A1/ABS(A1)×IF(MOD(ABS(A1)×10 000，1)＜0.5，ROUND(ABS(A1)，4)，(IF(MOD(ABS(A1)×10 000，1)＜0.6，(IF(MOD(ROUND(ABS(A1)，4)× 10 000，2)=0，ROUND(ABS(A1)，4)，ROUND(ABS(A1)，4)－ 0.000 1))，ROUND(ABS(A1)，4))))”

解决了上述两个难题，再运用简单的三角函数及加减运算，便可轻松在EXCEL上进行导线近似平差。当然，上述方法仍有一些瑕疵:

首先，负值角度在EXCEL中不能正确显示，虽然并不影响计算结果，但还是希望大家在以后的研究中能够进一步改进;

其次，由于不能在一个单元格中进行复杂的角度运算，表格中存在部分冗余数据(如 90°00'00″，180°00'00″)，使得表格整体感觉庞大;

再次，由于存在取位(近似值)问题，计算结果与理论值仍存在毫米级偏差，当然以目前测量所能达到的精度标准来说，完全可以忽略不计。