近距爆破源振动采集系统
2012-11-05张晶威孟立凡
张晶威, 孟立凡
(仪器科学与动态测试国防重点实验室,中北大学, 太原 030051)
0 引言
炸药在岩土介质中爆炸以后,有一部分能量转化为地震波[1-2]。通常认为,炮孔内药包爆炸产生的冲击波在距离药包半径150倍以外区域衰减为弹性波,并继续向远端传播,即形成地震波[3]。爆破地震波信号是时变-非平稳信号的特点,其频谱范围很宽[3-5]。随着爆破器材水平的提高,特别是电子雷管的出现,爆破技术得到了快速发展。爆破振动监测也从单纯的爆破振动安全评估转变为利用振动测量分析爆破振动特性,以期优化爆破方案,指导爆破工程实践。
为了更好获得爆破振动信号的特点,尽可能减少由于信号自身衰减[6]、环境因素等对检测结果的干扰,所以在距离爆区较近的地点进行地震波数据的采集是十分必要的。本文根据爆破工程实际需要开发了爆破近场振动监测系统,采集爆区近场的爆破振动信号,为更好的控制爆破振动,消除爆破振动危害,深入开展工程爆破理论研究提供数据支持。
1 近场爆破振动信号采集系统设计
1.1 近距爆破区振动信号的特点
爆破地震波从爆源到地面的传播过程中,随着距离的增大,波振面的扩大,和内阻尼的吸收,地震波的能量与振动幅度不断衰减[3],而在近场范围内测量得到的信号其能量幅值高,在介质中传播的距离短,受介质条件的影响小,能较清楚地反应振动的波动特性。通常可以将大地视为低通滤波器,地震波中的高频成分随着距离的增加会逐渐衰减消失。相比较而言在近距离范围内采集得到的振动信号包含的频率成分更完整,更能反映爆破振动的特点。
1.2 工程爆破拾振器原理及应用分析
1.2.1 振动速度拾振器原理
振动测试的拾振器,其力学模型是有阻尼单自由度系统力学模型,如图1所示。
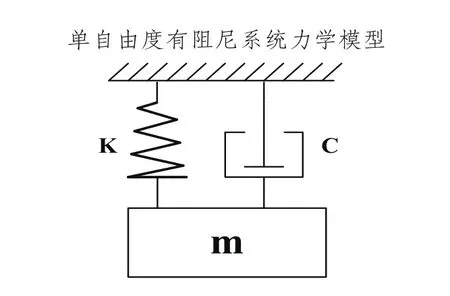
图1 有阻尼单自由度惯性振动传感器力学模型
图中,K为弹簧的弹性模量,C为系统的阻尼,m为质量块的质量。该系统的固有频率Ω=,根据被测信号的频率ω和系统固有频率Ω的关系,系统构成了位移计,加速度计[7-8]。表1给出了系统构成位移计和加速度计的条件。图2反映了目标采集信号频率ω与传感器频率Ω的关系。

表1 振动测试传感器(拾振器)的参数约束
目前工程上常见的动圈式磁电速度拾振器是基于位移计模型的传感器,是一个典型的高通型传感器[9],其幅—频特性如图3所示。

图2 固有频率与目标频率的关系
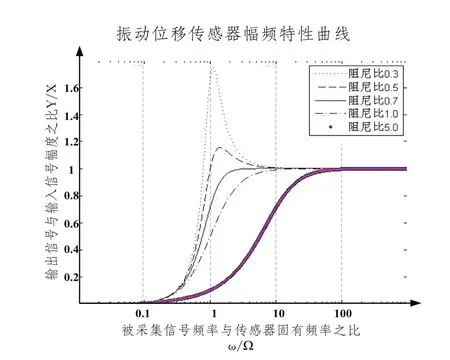
图3 振动位移计模型的动态特性参数曲线
传感器中的磁电式换能器(微分网络),根据法拉第电磁感应定律e=Blvsinθ(B为磁感应强度,l为导体长度,v为导体的运动速度,sinθ为导体与磁感线的夹角),换能器将位移量微分,得到速度v与输出电动势e的关系。此类传感器适合测量地震波中的低频信号,工程上使用的这种传感器的固有频率Ω制作得很低(1 Hz左右),根据Ω=可知,该传感器的质量块m较大,相应传感器体积也较大。理论上基于高通型位移计[9]原理的传感器可以测量很高频率的信号,但是由于仪器机械结构和寄生振动频率等限制,测量的频率也不能达到很高,另外传感器阻尼杯与动圈存在互感,测量高频信号情况下传感器灵敏度将会下降[7-8],一般测量范围在5~500 Hz左右。
1.2.2 近爆区域振动拾振器选型与动态特性参数分析
由于在爆区近距离测量得到的振动信号的高频成分能量较高,另外在本测试系统的设计中,希望采集、并研究信号的高频成分,结合传感器的静态、动态参数分析,选择了振动加速度传感器作为测量、测试系统的拾振器。
鉴于地震波信号时变、非平稳随机信号的特点,下面着重讨论振动传感器的动态特性,图5是加速度传感器的幅—频,相—频特性曲线,系统阻尼比不同,呈现出曲线族。
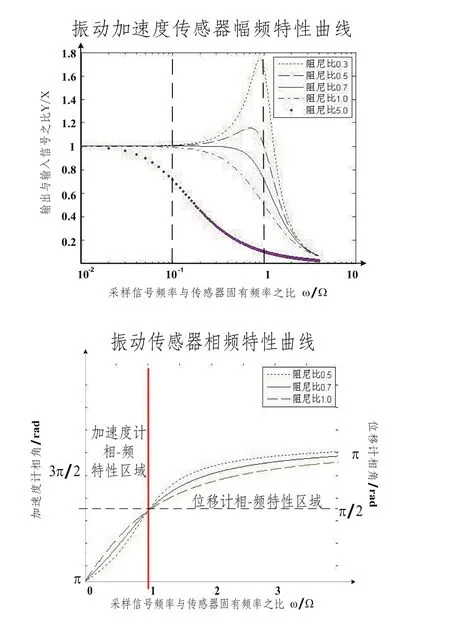
图5 传感器的动态特性参数曲线
(1)振动加速度传感器的幅—频特性
由上文所述的振动加速度传感器测试信号范围,结合幅频特性曲线可知,使用振动加速度传感器进行测试,当选择了合适的系统阻尼比(对不同原理的传感器的阻尼比ξ不同,例如电阻应变式一般选择0.6~0.7之间,压电式加速度传感器的阻尼比在 0.01~0.04 范围),使被采集信号频率与系统固有频率比Ω为ω的5倍以上范围,进行信号采集,其输出与被采集信号量的比值为定值,即保证了输入与输出关系是线性的。因为加速度传感器的固有频率Ω可以做到比较高的范围,故被采集信号的频率范围扩大了。但是传感器的固有频率与灵敏度是一对矛盾的参数,需要根据被采集信号的特点综合考虑。
(2)振动加速度传感器的相—频特性
由图5中振动传感器的相—频特性曲线可知,对于加速度传感器而言,选择合适的阻尼比,可以满足采集数据近似线性相位的相移(ξ=0.6~0.7)或几乎无相移(ξ取值在0.02左右[8]),保证了数据在不同频率采集无畸变,这是位移计不具备的特性。
2 振动采集节点结构设计
对具有高频能量分量的时变、非平稳随机信号进行采集,设计的信号采集节点需要较高共振频率的传感器。同时,针对微差爆破技术研究,对采集信号的相位精度要求较高,波形畸变小。另外系统的时间精度要求包括了采集节点自身精度,也包括多个采集节点之间的时间同步性,用于系统组网后测量地震波传播速度。
2.1 传感器选型
本系统设计拟使用美国Analog Device , Inc.公司的一款MEMS传感器ADXL001-70,图6为该传感器幅频响应特性曲线及一个微结构单元原理图[10]。
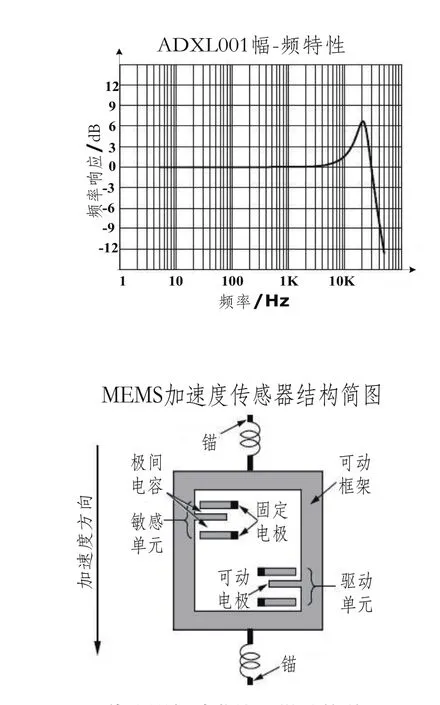
图6 传感器频响曲线及微结构单元原理图
采用完全的差分结构传感单元降低了电磁噪声。使用该传感器,设计成与数据记录仪的一体化的采集系统。应注意的是传感器焊接在电路板的方向及电路板与仪器外壳的耦合良好,杜绝机壳与电路板的相对移动。
2.2 系统的时间精度
实现系统的时间精度要求通过两个步骤进行控制。由于采集地点的复杂环境,设计的采集系统通过以下两步保证系统整体的时间精度。
①采集节点中设计了μs级精度的时钟模块(GPS模块),并在采集节点中设计一个时钟模块的触发接口。在采集节点布置之前,系统中的所有采集节点通过同步触发方式,校对时钟,保证系统初始工作的时间一致性。
②系统内部利用FPGA设计一套反馈校准的数字钟系统,保证采集系统工作过程中的时间精度。
2.3 数据采集节点框图
图7所示为数据采集系统的结构框图,此系统可以在宏观结构上可以分为信号采集部分部分和数字化小型数据记录仪部分,图中信号采集通道只画出一路,数据记录仪以FPGA为核心,实现多路信号采集,时钟反馈校准,数据传输,通信等功能,利用Altera NiosII软核处理器将CPU与外围数字逻辑控制结合成为SOPC,使用Flash芯片实现数据记录并对FPGA进行初始化配置等功能。
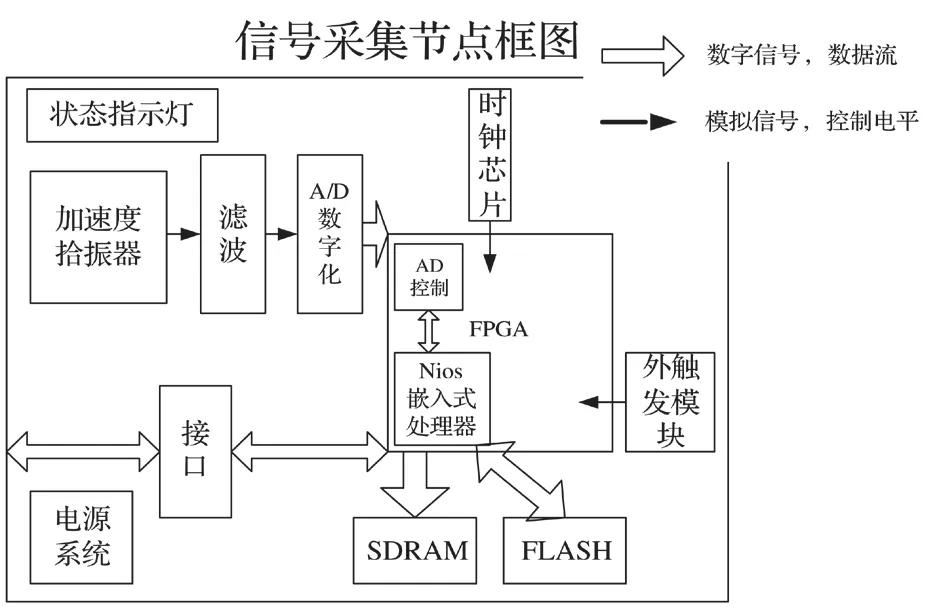
图7 信号采集节点框图
节点设置了内、外触发功能。在设定的电平值范围以外,节点数据循环刷新记录,当节点被触发后,系统一次性记录,不再刷新,并设定了负延时的长度,以记录信号的波头文件[11-12]。
3 工程案例
图8为某爆破工程单次炮孔布置及振动数据采集点设置图。数据采集点距爆区26 m,第1组炮孔2发,孔间延期为10 ms;第二组炮孔3发,孔间延期为17 ms,第三组炮孔4发,孔间延期为25 ms,第四组单孔,组与组之间,间隔150 ms,试验所用雷管为延时精确的电子数码雷管。被测爆区的东侧安置了一个振动采集节点。图9是使用本系统记录的振动波形。从图上可以清晰地将各组振动波形从时间上区分开,证明系统的动态性能良好,实现了在近距离记录振动变化的目的。

图8 某工程炮孔布置及振动数据采集点示意图
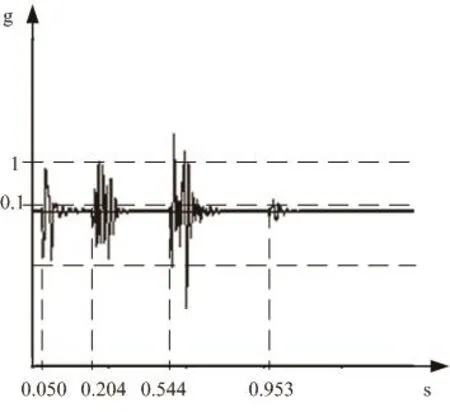
图9 某工程采集振动数据
4 总结
本文结合爆破振动近场信号的特点,分析爆破振动信号采集的拾振器原理,提出了一种爆区近距离范围内振动采集设备的设计方案,为爆破振动研究提供了得力的工具。
节点可以灵活的布置在爆破振动测试区域,根据不同的测试目标组成不同的测试方案。本测试系统尚处于研制阶段,其系统组网需要进一步的深入。
[1] 张雪亮,黄树堂.爆破地震效应[M].北京:地震出版社,1981.
[2] 孟吉复,惠新斌.爆破测试技术[M].北京:冶金工业出版社,1992.
[3] 李夕兵,凌同华,张义平.爆破震动信号分析理论与技术[M].北京:科学出版社,2009.
[4] 何军,于亚伦,梁文基.爆破振动信号的小波分析[J].岩土工程学报,1998,20(1):47-50 .
[5] 林大超,施惠基,白春华.爆炸地震效应的时频分析[J].爆炸与冲击,2003,23(1):31-35.
[6] 顾毅成,史雅语,金骥良.工程爆破安全[M].合肥:中国科学技术大学出版社,2009.
[7] 铁道部铁道科学院.振动测试与分析[M].北京:人民铁道出版社,1978.
[8] 李德葆,陆秋海.工程振动试验分析[M].北京:清华大学出版社,2004.
[9] 严普强,乔陶鹏.工程中的低频振动测量与传感器[J].振动、测试与诊断,2002,22(4):247-253.
[10] Analog Device Inc.High Performance Wide Bandwidth Accelerometer.[EB/OL].[2011-3-13].
[11] http://www.analog.com/zh/mems/high-gaccelerometers/adxl001/products/product.html.
[12] 原彦飞,尤文斌,李新娥.运用NAND闪存的负延时存储测试系统[M].仪器仪表学报,2006,27(6):1517-1518.
[13] 赵纯,裴东兴.水下爆炸冲击波测试系统的设计与实现[J].计量与测试技术,2009,36(2):36-37.
[14] 杨年华,林世雄.爆破振动测试技术探讨[J].爆破,2000,17(3):90-92.
