基于流固耦合理论某尾矿坝失稳特性及稳定性分析
2012-11-05张力霆齐清兰周占磊
李 强,张力霆,齐清兰,周占磊
(1. 石家庄铁道大学 土木工程学院,石家庄 050043; 2. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,石家庄 050043)
1 引 言
全世界每年采出金属和非金属矿石、煤、砂砾等约90×108t,相应排弃废石和尾矿约300×108t[1],采用尾矿坝堆存尾矿仍是目前主要的处理方法。尾矿坝稳定性不仅涉及到矿山自身的生产安全和经济效益,而且与库区下游居民的生命财产及周边环境息息相关,2008年我国山西临汾铁矿尾矿坝失稳溃坝事件造成了巨大的人员伤亡,所以研究尾矿库的稳定性具有重要的意义[2]。
目前对尾矿坝的稳定性研究以极限平衡法为主,尾矿库安全技术规程[3]建议采用极限平衡法对尾矿库的抗滑稳定性进行分析,但采用极限平衡分析时,往往需要引入假设:不考虑滑体的变形,假设滑裂面的形状和初始滑裂面的位置等,同时,在极限平衡分析时还需要事先计算出尾矿坝中浸润线的位置,导致渗流场计算与稳定分析计算不同步,容易导致人为的计算误差。
强度折减法是分析边坡稳定性的另一种方法,最大优点是不需要假设滑裂面的形状和初始滑裂面的位置,随着计算机和计算方法的进步,该方法得到迅速发展。目前强度折减法主要应用在边坡和土石坝的稳定性分析[4-7],在尾矿坝稳定性研究中运用很少。与一般的土坡相比,尾矿坝中存在渗流场,分析其稳定性需要考虑土水相互作用,即涉及到流固耦合问题,给强度折减计算带来了难度[8-13]。与土石坝相比,尾矿库也有自身特殊性,主要表现在:(1)尾矿坝是透水性坝体,其堆积材料尾矿砂更接近于砂土的性质,土石坝大多是黏土坝,砂土形成的边坡更易发生流滑破坏,而黏土形成的边坡一般是深层滑弧滑动破坏;(2)尾矿坝的坝面坡度远小于土石坝的坝面坡度,使得尾矿坝坝体失稳滑动前往往经过较大的变形;(3)尾矿坝一般建在山谷中[14],所处的地形远比土石坝复杂,使尾矿坝的潜在滑动受到地形的影响。以上因素导致尾矿坝潜在滑动破坏模式与普通的边坡或土石坝不同,具有自身的特殊性,需要单独研究。
采用强度折减法研究尾矿坝的稳定性,除了要考虑流固耦合对分析带来的难度外,还需要分析强度折减中另一个关键的问题,即强度折减过程中尾矿坝失稳判据的选择问题。在普通边坡稳定分析中,所取的准则往往是数值计算不收敛[15],但考虑影响数值计算不收敛的因素较多,如数值计算方法本身的稳定性、计算模型网格质量、计算模型是否存着异常的局部应力集中等。尾矿库大多建立在山谷 中,地形复杂,容易造成网格质量及地形突变处局部应力集中,对数值计算收敛性造成影响。
本文采用流固耦合-强度折减法相结合的方法,选取典型的工程实例,得出了现状尾矿坝渗流场与应力场,根据实测资料,验证了流固耦合计算的正确性。在此基础上,研究不同工况下该尾矿坝的失稳破坏模式,提出尾矿坝常见的两种滑动失稳模式,分析了这两种破坏模式对应的塑性区发展贯通特征及影响因素,确定折减过程中尾矿坝失稳准则,计算尾矿坝体安全系数,并与极限平衡法计算结果对比分析,验证强度折减法对尾矿坝稳定分析适用性,结合规范建议了强度折减法的临界安全系数值,对现状尾矿坝稳定性进行了评价。
2 流固耦合-强度折减理论
尾矿库的坝体中存在着渗流场,渗流场的自由液面即浸润面,浸润面下方为饱和土,浸润面上方存在着非饱和土,因此尾矿库中渗流场和应力场耦合计算的基本理论为非饱和流固耦合理论,在不考虑温度和化学作用的非饱和土流固耦合微分方程组主要包括平衡方程、连续方程、基质吸力方程[12-13],其中平衡方程为
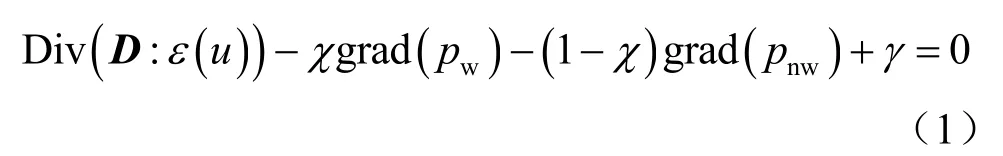
式中:D为刚度矩阵;ε(u)为应变矩阵;χ为非饱和土参数;pw为孔隙水压力;pnw为孔隙气压力;γ为重度。
考虑到水在土中的渗流问题,将达西定律与质量守恒方程结合起来,可得连续性方程:
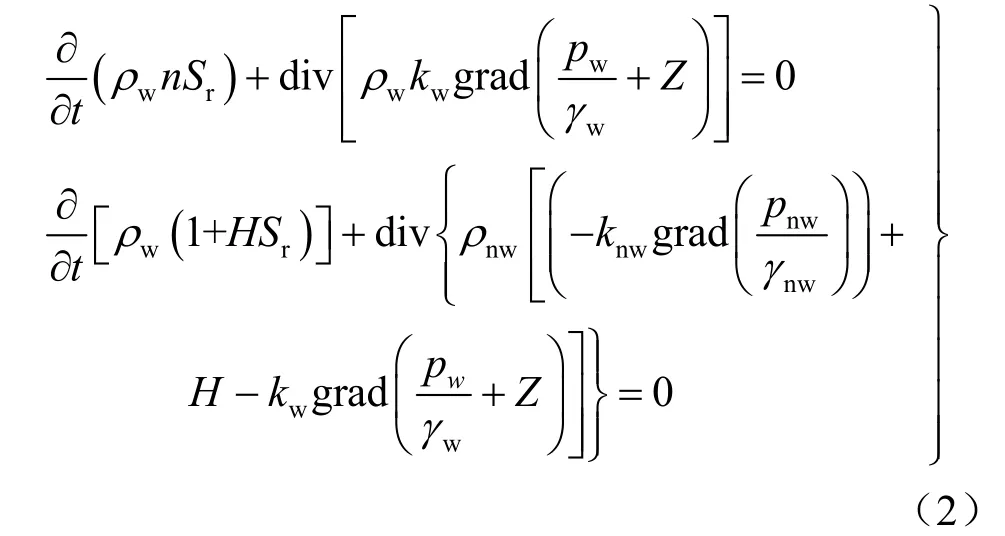
考虑到非饱和土的渗透系数与土体的饱和度和体积含水率有关,需要引入土-水特征曲线方程:
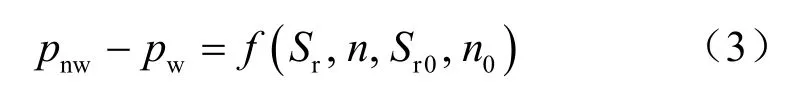
式中:Sr为饱和度;kw、knw分别为水、气渗透系数;Z为位置水头;n为孔隙率;H为henry系数。
采用式(1)~(3),结合初始和边值条件可以计算出尾矿库中有效应力场和孔隙水压力场的分布规律,从而结合强度折减法对尾矿库的稳定性做出评价。
强度折减法于20世纪70年代提出,但由于计算力学尚处起步阶段和缺乏相应的失稳判据等原因,长期以来并没有得到岩土界的广泛认可[16]。1999年Grififth等[17]采用有限元强度折减法得到的稳定安全系数与传统方法的计算结果比较接近,引起了国内外学者广泛关注,表明采用此方法分析边坡稳定性是可行的。如果土的破坏准则采用摩尔-库仑,则强度折减法的基本公式为
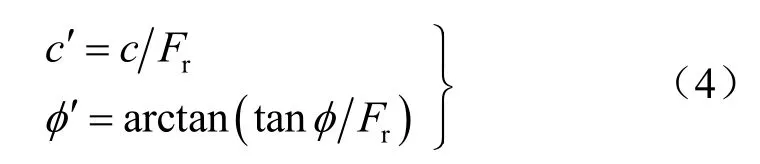
式中:Fr为折减系数。当尾矿坝失稳时对应的折减系数Fr即为安全系数Fs。
大型有限元软件 ABAQUS中自带有流固耦合模块,单元库中有专用于流固耦合分析的孔压单元,采用 ABAQUS内置命令可以实现尾矿坝上下游各种边界条件的设置,从而实现流固耦合分析,ABAQUS中本身不包含强度折减功能模块,但在流固耦合分析过程中,通过添加折减系数状态变量间接实现流固耦合和强度折减耦合计算。
3 工程实例及计算工况
3.1 工程实例
河北省承德县某尾矿库位于承德县一条呈“V”字型的山间沟谷内。该尾矿库现状堆积坝堆积高度为54.2 m,平均外坝坡比约1∶4.5,初期坝为粉质黏土坝,坝高28.3 m,坝顶宽约4.0 m,内外坝坡坡比均为1∶2.5,初期坝坝趾位置设有排渗棱体,排渗棱体为碎石混合体筑成。尾矿库正常运行下干滩长度为340 m,为了增强初期坝的抗滑稳定性,在尾矿库运行后期对初期坝进行反压坡处理,尾矿库级别为三等。
尾矿库库区周围山体地貌属低山丘陵地貌,库区基岩主要为斜长岩及片麻岩,尾矿库堆积材料以尾矿砂为主。尾矿库现状库区如图1所示。图中,1-1′断面为主勘探断面,勘探中发现浸润线埋深最小为3 m,为了以后该尾矿库加高扩容,拟在初期坝上进行二次压坡处理。
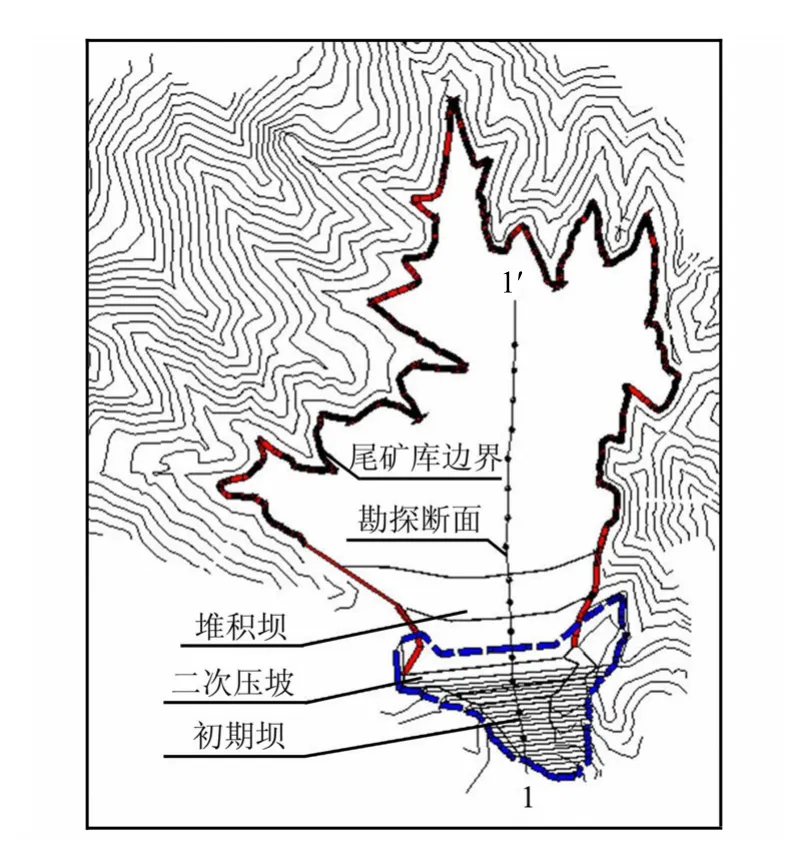
图1 尾矿库平面图Fig.1 The planimetric map of tailing pond
3.2 计算工况
为了分析现状坝体及二次压坡后坝体的稳定性和研究尾矿坝强度折减中的失稳判据,分析尾矿坝潜在的滑移失稳特性,本文共计算了4种工况,如图2所示。图中,工况1为现状尾矿库1-1′断面,工况2为二次压坡后的尾矿库1-1′断面,工况3、4是为了研究而虚拟的工况,工况3坝底为平坡,通过工况1和工况3对比可以反映地形对尾矿坝稳定性的影响,工况4中初期坝为碎石初期坝,相比工况1,工况4初期坝透水性强,浸润线的埋深浅,通过对比工况1和工况4可以反映浸润线埋深对尾矿坝稳定性的影响。
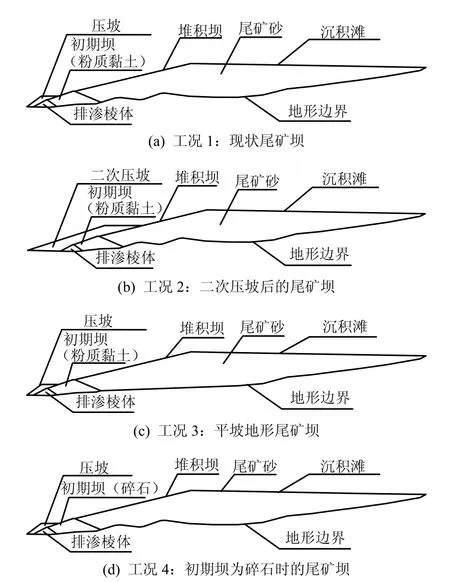
图2 计算工况Fig.2 Calculate models
根据以上4种工况建立有限元模型,其中初期坝面、堆积坝面、压坡面、沉积滩面为透水边界,尾矿库坝底为不透水边界,并在坝底设置水平和竖直方向的位移边界约束,上游水位按干滩长度确定,下游水位设在压坡最底处,尾矿库相应的材料参数如表1所列。
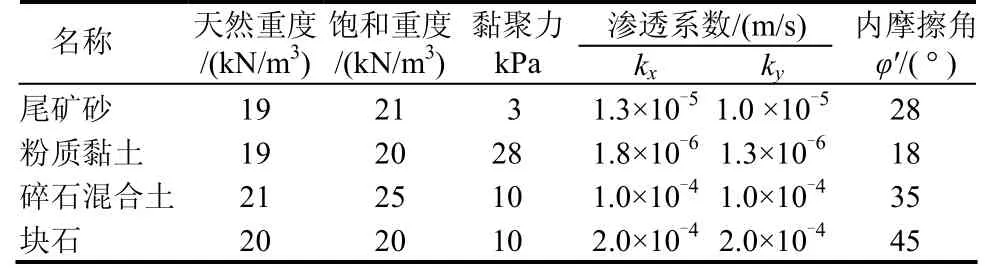
表1 物理力学参数Table1 Physico-mechanical parameters
4 计算结果
采用流固耦合-强度折减法计算坝体浸润线的埋深,得到强度折减过程中尾矿坝内塑性区的发展过程,并在Stab2005平台上采用瑞典圆弧法和毕肖普法计算了各工况的安全系数。
工况 1:浸润线计算结果见图 3,图中有色和无色交界面为浸润线(下文同)。强度折减计算结果和极限平衡法计算结果见图4、5。图中,x为尾矿坝长度;y为高度初始滑裂面2.140为安全系数;临界滑面1.5991为最小安全系数,图8、11、14同。工况 2:浸润线计算结果、强度折减计算结果、极限平衡法计算结果见图6~8。工况3:浸润线计算结果和强度折减计算、极限平衡法计算结果如图9~11所示。工况4:浸润线计算结果、强度折减计算结果如图12、13所示。
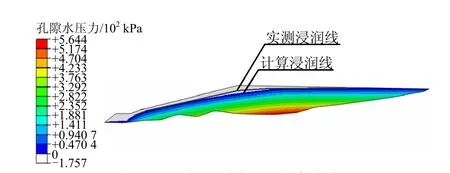
图3 现状尾矿坝浸润线分布Fig.3 Status of saturated line in tailing dam of model-1
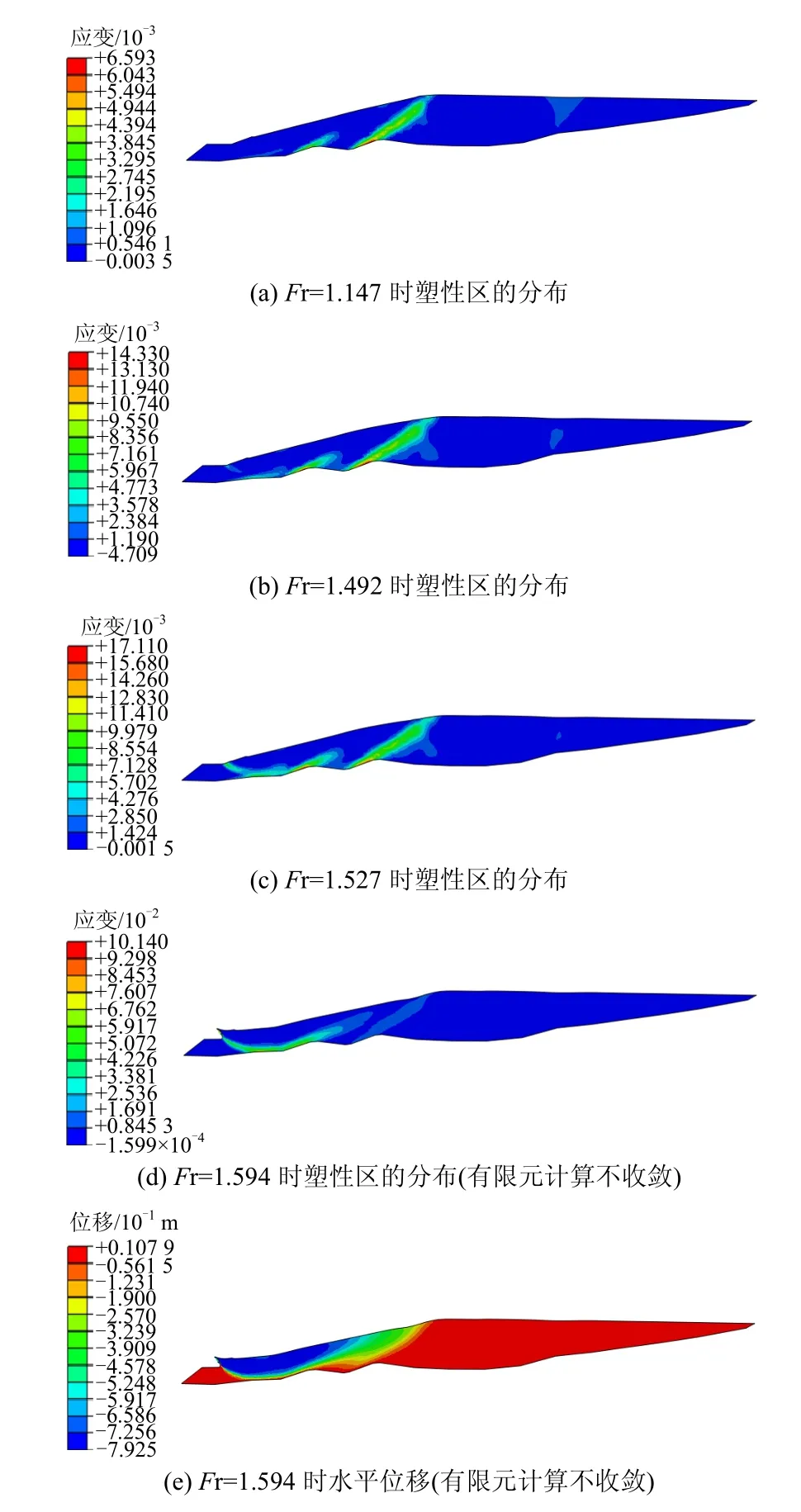
图4 工况1尾矿坝强度折减计算结果(变形放大30倍)Fig.4 Model-1 tailing dam strength reduction calculation results
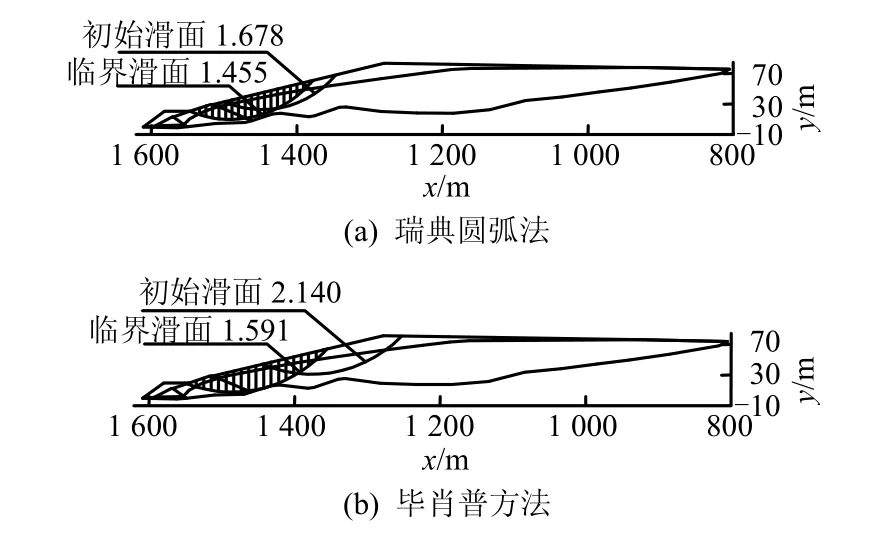
图5 工况1极限平衡法计算结果Fig.5 Results of model-1 by limiting equilibrium methods
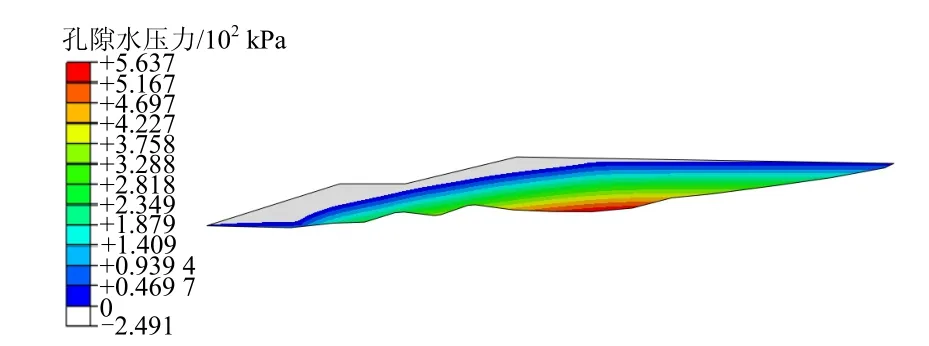
图6 工况2尾矿库浸润线分布图Fig.6 Saturated line distribution in tailing dam of model-2
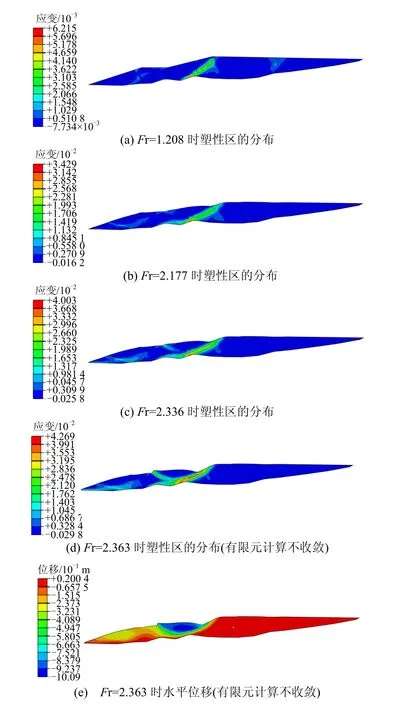
图7 工况2尾矿坝强度折减计算结果(变形放大30倍)Fig.7 Model-2 strength tailing dam strength reduction calculation results
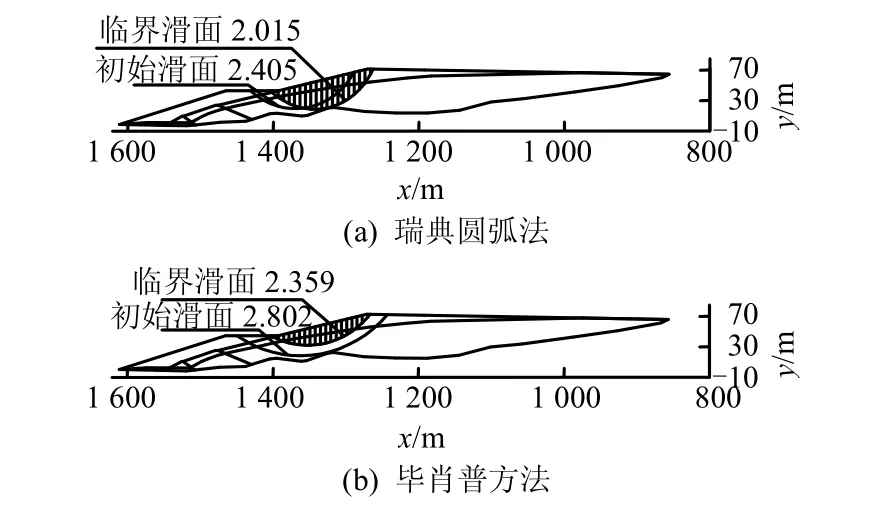
图8 工况2极限平衡法计算结果Fig.8 Model-2 limiting equilibrium calculation results
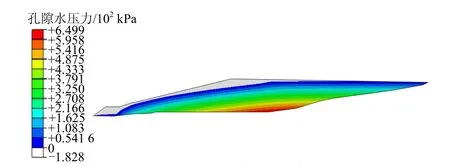
图9 工况3尾矿库浸润线分布图Fig.9 Saturated line distribution in tailing dam of model - 3
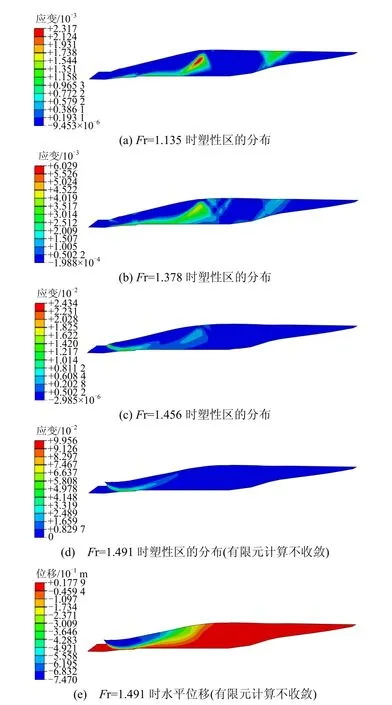
图10 工况3尾矿坝强度折减计算结果(变形放大30倍)Fig.10 Model-3 tailing dam strength reduction calculation results
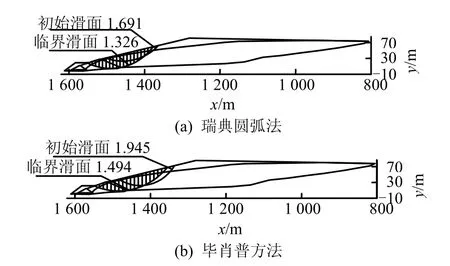
图11 工况3极限平衡法计算结果Fig.11 Model-3 by limiting equilibrium calculation results
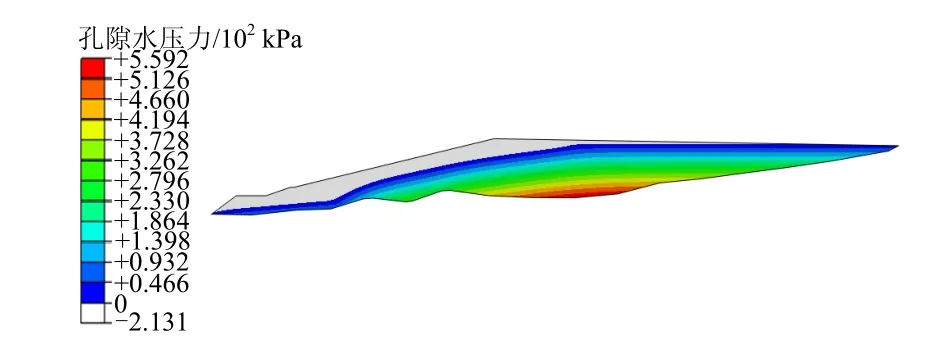
图12 工况4尾矿坝浸润线分布Fig.12 Saturated line distribution in tailing dam of model - 4
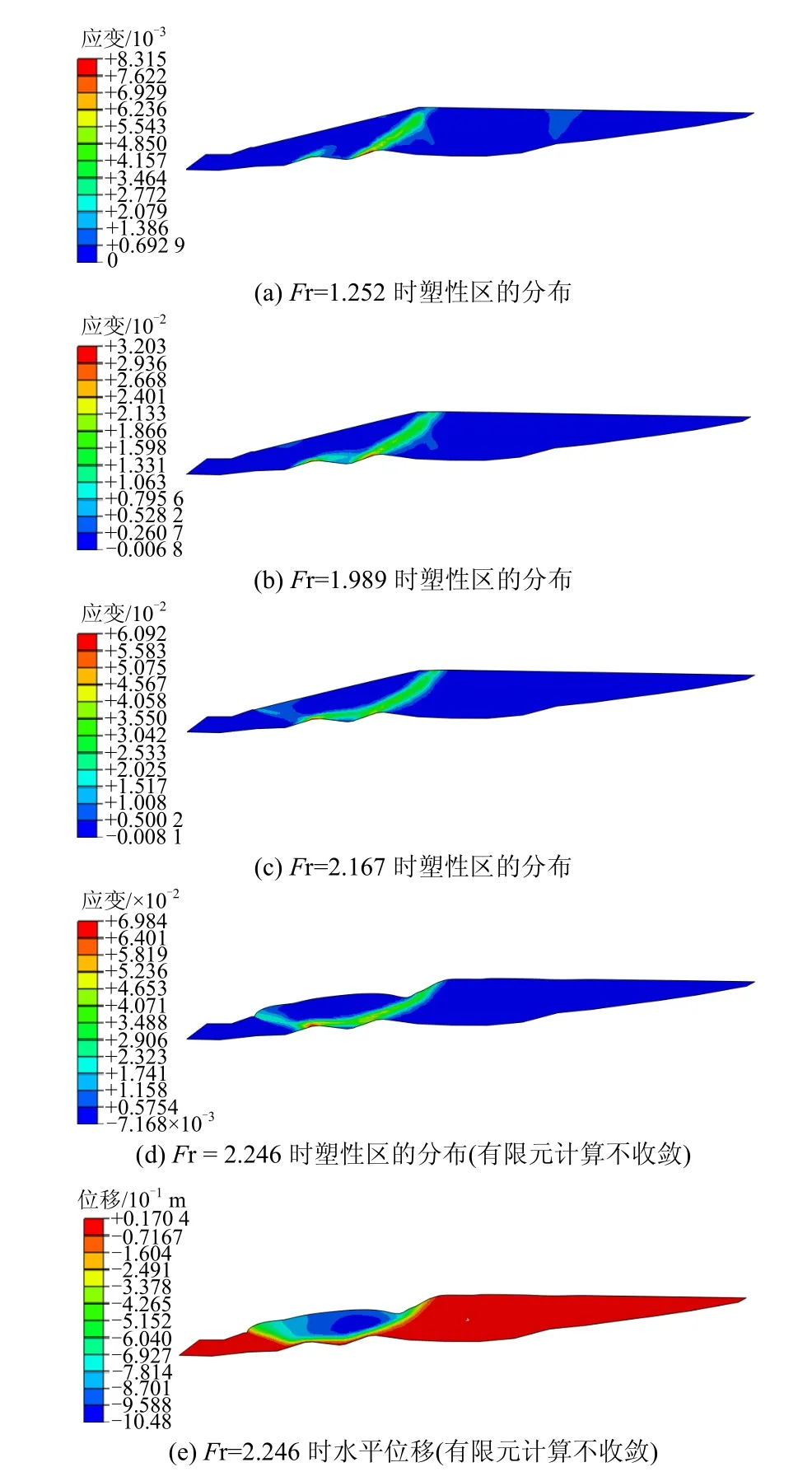
图13 工况4尾矿坝强度折减计算结果(变形放大30倍)Fig.13 Model-4 tailing dam strength reduction calculation results
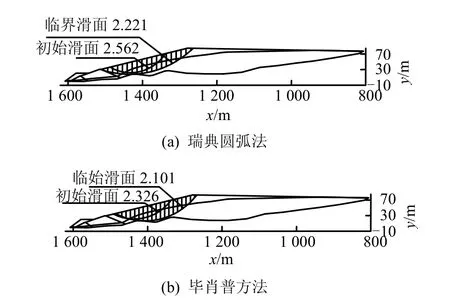
图14 工况4极限平衡法计算结果Fig.14 Model-4 limiting equilibrium calculation results
5 计算分析
5.1 强度折减法分析尾矿坝稳定性适用性评价
5.1.1 强度折减法确定尾矿坝安全系数准则
采用强度折减法计算安全系数时,折减过程中坝体失稳判据非常重要,目前失稳判据主要有 3种:数值计算不收敛、塑性区贯通和位移出现突变[15-18]。
多数文献建议采用数值不收敛作为判据[15],但是,考虑到影响数值收敛的因素较多,如有限元网格质量或局部应力集中都可能导致数值计算不收敛,单纯采用有限元计算是否收敛可能带来误差。
如果采用塑性区是否贯通作为判断准则,从 4个工况计算结果来看,由于塑性区图形显示问题,如从图4(c)、12(c)中很难判断塑性区是否已经贯通,这种判断方式容易由于主观因素带来误差。对于尾矿库,由于堆积坝坡比较小,尾矿坝中潜在滑移面在发展过程中,滑体可能已经发生较大的变形,导致位移突变不是十分明显,见图7(e)、13(e),实际判断起来难以准确确定滑裂面的位置。
运用强度折减确定尾矿坝安全系数时,不宜单独采用一种判别准则来判断,4种工况计算结果表明,宜以有限元是否收敛为主,以塑性区是否贯通作为校核,共同确定尾矿坝的安全系数。
5.1.2 强度折减法确定尾矿坝安全系数适用性
采用流固耦合-强度折减对 4种工况下的尾矿坝稳定性进行了分析,确定了各种工况下尾矿坝的渗流场和安全系数。
对于尾矿坝的渗流场,现状尾矿坝(工况 1)有浸润线实测资料,通过现状尾矿坝实测资料与数值计算结果对比可以看出(图3),计算结果与实测资料吻合很好,表明数值模拟有效性。对于尾矿坝的抗滑稳定性,4种工况强度折减法计算结果和极限平衡法计算的安全系数见表2。

表2 3种方法计算的安全系数Table2 Safe factors by limiting equilibrium methods and strength reduction method
表2中,强度折减法和 Bishop法的计算结果最小相对误差为0.2%,最大相对误差为1%。比较强度折减法与瑞典圆弧的计算结果,最小相对误差为6%,最大相对误差为14%,工况2误差最大。
从图 7(d)、8(a)可以看出,强度折减法计算出的滑裂面位置与瑞典圆弧法确定的滑裂面位置相差较大,是由于两种方法得出安全系数差异较大,强度折减法得出的滑裂面位置较浅,而瑞典圆弧法得出的临界滑弧位置较深,已经到达坝底。总体而言,强度折减法与Bishop法计算出的安全系数接近,与瑞典圆弧法计算出的安全系数相差相对较大,采用强度折减分析坝体稳定性时,建议参照规范中所规定的Bishop法对应安全系数的临界值。
此外,强度折减法得出的塑性贯通区与Bishop法得出的临界滑弧更为接近,与瑞典圆弧法得出的临界滑动面位置较为接近。
5.2 现状尾矿库稳定性评价
通过对现状尾矿坝的稳定性分析,计算所得抗滑安全系数满足规范的要求,但得出现状尾矿坝浸润线埋深最小值为3.3 m,实测值为3 m,这个值小于相关规范对最小埋深的要求。需要进行整治,考虑到该尾矿库所处的地形,该尾矿库有后续加高的潜力,拟采用二次压坡对现状进行处理,处理后的尾矿坝的最小埋深为7.2 m,其安全系数为2.363,满足相关规范的规定。
5.3 尾矿库坝体潜在破坏模式及影响因素
5.3.1 折减过程中尾矿库的塑性区贯通
从图2~13可以看出,强度折减过程中塑性区的扩展贯通过程可以概括为4个步骤:
①在坝体内部出现了局部塑性区,塑性变形较小,工况1、4中出现了两个塑性区,见图4(a)、13(a),而工况 2、3出现了一个塑性区,见图 7(a)和 10(a),对比工况 1和工况3可知地形对局部塑性区的出现影响较大。
②4种工况中,塑性区沿着地形发展,见图4(b)、7(b)、10(b)、13(b),表明尾矿坝有沿地形流滑的发展趋势。
③尾矿坝坝体内塑性区沿着地形进一步发展,同时,尾矿坝压坡体和坝体交界附近出现了新的局部塑性区,见图 4(c)、7(c)、10(c)、13(c)。
④以上两种局部塑性区贯通,塑性应变增大,导致有限元计算不再收敛,见图4(d)~4(e)、图7(d)~7(e),图 10(d)~10(e)和图 13(d)~13(e)。
通过以上分析可知,工况1、3的塑性区贯通模式与工况2、4贯通模式明显不同。在工况1、3中,塑性贯通区位于尾矿坝一部分区域,整个潜在滑动体属于尾矿坝的一部分,该潜在破坏属于局部滑动破坏,见图 4(d)、10(d)。而工况 2、4中,塑性贯通区贯通了整个尾矿堆积坝,该潜在滑动面会导致整个坝体的滑动,属于整体滑动破坏。在初期坝(或压坡)抗滑稳定性满足要求的情况下,尾矿坝可能发生局部失稳和整体失稳。
5.3.2 尾矿库坝体两种滑移模式影响因素
由于影响尾矿坝失稳的因素较多,对于同种材料而言,尾矿坝的坡比、浸润线分布和地形因素对尾矿坝抗滑稳定性影响最大。工况1、3中潜在滑动模式均为局部滑动,地形不同,但浸润线埋深都较浅,其他的条件都相同,表明地形并不是导致局部滑动的决定性因素。相比工况1与工况4,地形相同,而浸润线埋深不同,工况1浸润线埋深浅,出现了潜在局部滑动模式,工况4浸润线埋深较深,出现了潜在的整体滑动模式,说明尾矿坝材料和坡比相同情况下,浸润线埋深浅是导致工况1尾矿潜在局部滑动破坏的主要原因。
6 结 论
(1)流固耦合-强度折减法可以用于尾矿库的抗滑稳定性分析,计算所得浸润线埋深与实测资料吻合,确定的安全系数与毕肖普方法得出的安全系数接近,建议采用强度折减分析尾矿坝稳定性时参照相关规范中Bishop法对应的临界安全系数。
(2)采用流固耦合-强度折减法计算安全系数时,建议采用有限元不收敛为主、塑性区贯通为校核作为判断准则。
(3)尾矿坝潜在失稳模式有两种:一种是潜在的局部滑动,另一种是潜在的整体滑动,在尾矿坝浸润线埋深较浅时易发生局部滑动,较深时易发生整体滑动。
[1]郭振世. 高堆尾矿坝稳定性分析及加固关键技术研究[博士学位论文D]. 西安: 西安理工大学,2010.
[2]齐清兰. 尾矿库渗流场的数值模拟与工程应用[M]. 北京: 中国水利出版社,2011.
[3]国家安全生产监督管理总局. AQ2006-2005 尾矿库安全技术规程[S]. 北京: 煤炭工业出版社,2005.
[4]郑颖人,赵尚毅,孔位学,等. 岩土工程极限分析有限元法[J]. 岩土力学,2005,26(1): 163-168.ZHENG Ying-ren,ZHAO Shang-yi,KONG Wei-xue,et al. Geotechnical engineering limit analysis using finite element method[J]. Rock and Soil Mechanics,2005,26(1): 163-168.
[5]连镇营,韩国城,孔宪京. 强度折减有限元法开挖边坡的稳定性[J]. 岩土工程学报,2001,23(4): 407-411.LIAN Zhen-ying,HAN Guo-cheng,KONG Xian-jing.Stability analysis of excavation by strength reduction FEM[J]. Chinese Jounal of Geotechnical Engineering,2001,23(4): 407-411.
[6]赵尚毅,郑颖人,时卫民,等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报,2002,24(3): 343-346.ZHAO Shang-yi,ZHENG Ying-ren,SHI Wei-min,et al.Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Jounal of Geotechnical Engineering,2002,24(3): 343-346.
[7]郑宏,李春光,李焯芬,等. 求解安全系数的有限元法[J]. 岩土工程学报,2002,24(5): 626-628.ZHENG Hong,LI Chun-guang,LEE C F,et al. Finite element method for solving the factor of safety[J].Chinese Jounal of Geotechnical Engineering,2002,24(5): 626-628.
[8]唐晓松,赵尚毅,郑颖人,等. 渗流作用下利用有限元强度折减法的边坡稳定性分析[J]. 公路交通科技,2007,24(9): 6-10.TANG Xiao-song,ZHAO Shang-yi,ZHENG Ying-ren,et al. Analysis of soil slope stability by strength reduction element method under seepage[J]. Journal of Highway and Transportation Research and Development,2007,24(9): 6-10.
[9]刘俊新,刘育田,胡启军. 非饱和地表径流-渗流和流固体耦合条件下降雨入渗对路堤边坡稳定性研究[J].岩土力学,2010,31(3): 903-910.LIU Jun-xin,LIU Yu-tian,HU Qi-jun. Stability of embankment slope subjected to rainfall infiltration considering both runoff-underground seepage and fluid-solid coupling[J]. Rock and Soil Mechanics,2010,31(3): 903-910.
[10]周桂云,李同春. 基于非饱和土固结理论的有限元强度折减法[J]. 岩土力学,2008,29(4): 1133-1137.ZHOU Gui-yun,LI Tong-chun. FEM strength reduction method based on consolidation theories of unsaturated soils[J]. Rock and Soil Mechanics,2008,29(4): 1133-1137.
[11]张晓咏,戴自航. 应用 ABAQUS程序进行渗流作用下边坡稳定分析[J]. 岩石力学与工程学报,2010,29(增刊1): 2927-2934.ZHANG Xiao-yong,DAI Zi-hang. Analysis of slope stability under seepage by using ABAQUS program[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Supp.1): 2927-2934.
[12]张延军,王恩志,王思敏.非饱和土中的流-固耦合研究[J]. 岩土力学,2004,25(6): 999-1003.ZHANG Yan-jun,WANG En-zhi,WANG Si-jing. Study for fluid-solid coupling process in unsaturated soil[J].Rock and Soil Mechanics,2004,25(6): 999-1003.
[13]李培超,孔祥言,卢德唐. 饱和多孔介质流固耦合渗流的数学模型[J]. 水动力学研究与进展(A辑),2003,18(4): 419-426.LI Pei-chao,KONG Xiang-yan,LU De-tang.Mathematical modeling of flow in saturated porous media on account of fluid-structure coupling effect[J]. Journalof Hydrodynamics (Ser. A),2003,18(4): 419-426.
[14]路美丽,崔莉. 复杂地形尾矿坝的三维渗流分析[J]. 岩土力学,2006,27(7): 1176-1180.LU Mei-li,CUI Li. Three-dimensional seepage analysis for complex topographical tailings dam[J]. Rock and Soil Mechanics,2006,27(7): 1176-1180.
[15]赵尚毅,郑颖人,张玉芳,等.有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.ZHAO Shang-yi,ZHENG Ying-ren,ZHANG Yu-fang,et al. Study of slope failure criterion in strength reduction finite element method[J]. Rock and Soil Mechanics,2005,26(2): 332-336.
[16]郑颖人,赵尚毅. 岩土工程极限分析有限元法及其应用[J]. 土木工程学报,2005,38(1): 91-98.ZHENG Ying-ren,ZHAO Shang-yi. Limit state finite element method for geotechnical engineering analysis and its applications[J]. China Civil Engineering Journal,2005,38(1): 91-98.
[17]GRIFFITHS D V,LANE P A. Slope stability analysis by finite elements[J]. Geotechnique,1999,49(3): 387-403.
[18]栾茂田,武亚军,年廷凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报,2003,23(3): 1-8 LUAN Mao-tian,WU Ya-jun,NIAN Ting-kai. A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J]. Journal of Disaster Prevention and Mitigation Engineering,2003,23(3): 1-8.
