盾构隧道施工引起的土体初始超孔隙水压力分布研究

魏新江，陈伟军，魏 纲，洪 杰

（1.浙江大学 建筑工程学院，杭州 310058；2.浙江大学城市学院 土木工程系，杭州 310015）

1 引 言

由于盾构机的开挖、剪切、挤压等作用以及壁后注浆作用，会对周围土体产生扰动，形成超孔隙水压力区。同时实测资料表明，当盾尾通过后，超孔隙水压力达到峰值，随后消散，土体产生固结沉降[1－5]。本文定义最大超孔隙水压力为初始超孔隙水压力。对盾构施工引起的土体固结沉降研究，需要确定土体初始超孔隙水压力。因此，对盾构施工引起的土体初始超孔隙水压力研究至关重要。

关于初始超孔隙水压力的研究，魏纲[6]运用应力释放理论得到与衬砌相邻的拱顶处土体初始超孔隙水压力，进而研究工后沉降；张冬梅等[7]则将隧道上方 1 m的土层作为土体超孔隙水压力分布范围，运用应力路径法计算与衬砌相邻的隧道中心水平线处土体初始超孔隙水压力值，进而研究固结沉降；徐方京等[8－9]推导了与盾构挤推力有关的初始超孔隙水压力分布范围；Skempton[10]、Henkel[11]推导了有较多待定参数的初始超孔隙水压力公式。综上所述，现今的土体初始超孔隙水压力研究着重于衬砌相邻土体的某个点，并非周边所有与衬砌相邻的点，更非任一点土体，同时有较多待定参数，因此，有必要对此进行相关研究。

本文运用应力释放理论推导周边所有与衬砌相邻的土体初始超孔隙水压力计算公式，确定土体初始超孔隙水压力的分布范围，以及运用应力传递理论推导任一点土体初始超孔隙水压力计算公式，最后通过算例对此进行一定的解释。

2 土体初始超孔隙水压力的分布及计算

2.1 与衬砌相邻的周边土体初始超孔隙水压力计算

在研究周边所有与衬砌相邻土体初始超孔隙水压力计算方法时，假定：①土体初始超孔隙水压力由土体应力释放引起[6]；②所有与衬砌相邻的各点具有相同的应力释放率。

具体计算步骤如下：①计算隧道的法向围压[12]；②采用文献[7]应力路径法计算与衬砌相邻的隧道中心水平线处的土体初始超孔隙水压力，除以该点处的法向围压，得到应力释放率；③将隧道周边的法向围压乘以应力释放率，得到与衬砌相邻的周边土体初始超孔隙水压力值。

2.1.1 隧道法向围压计算

图1为盾构施工隧道普遍采用的修正惯用法受力模式[13]，本文主要研究黏土地层的受力情况，计算时采用水、土合算[14]。对于隧道上覆土层的受力情况，实测数据表明[15]，隧道拱顶部分土压力随时间延长而增加，最后十分接近于上覆全部土体重量。因此，不考虑拱效应的存在。

以隧道水平线为起始线，逆时针为正，θ为隧道某点与水平线的夹角。取隧道右半部分进行推导。

①当0≤θ＜π/4时，隧道法向应力σ为

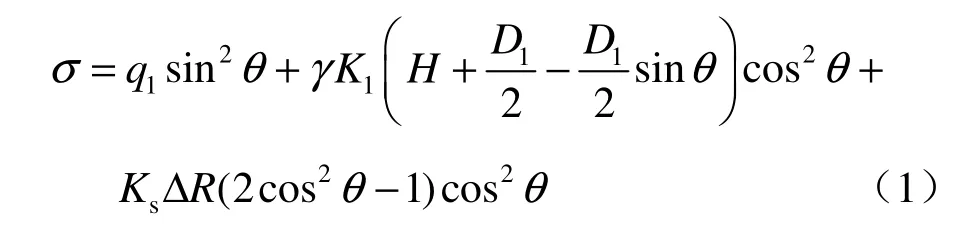
②当 π/4≤θ＜π/2时，隧道法向受力σ为

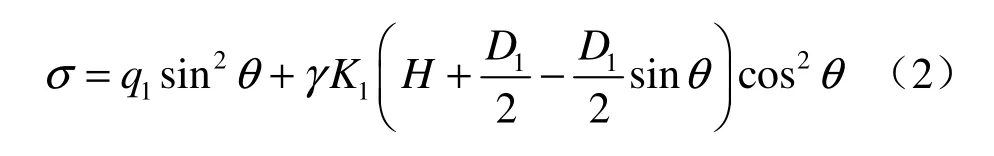
③当3π/2≤θ＜7π/4时，隧道法向受力σ为

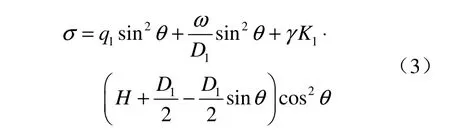
④当7π/4≤θ＜2π 时，隧道法向受力σ为

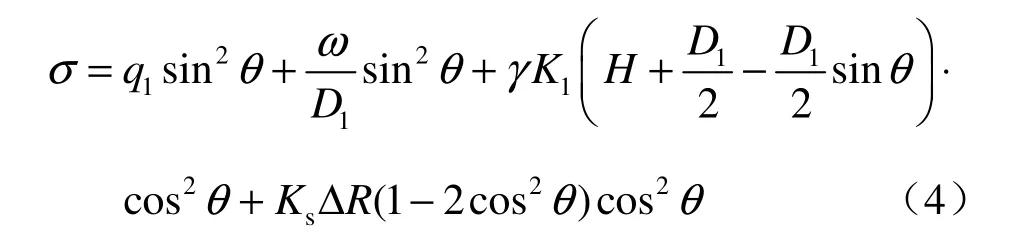
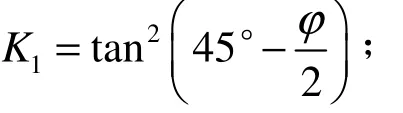
图1 隧道受力模式Fig.1 Diagram of tunnel forced model

2.1.2 隧道中心水平线处土体初始超孔隙水压力计算

根据文献[7]上的p′-q（见图2）知，OS方程为

OS′直线方程为

同时SS′曲线符合方程为

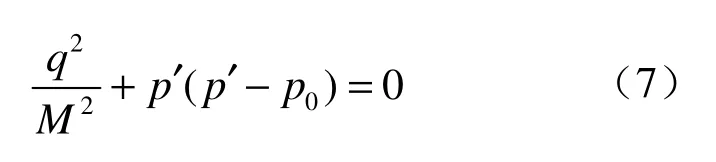
通过以上方程可以推导与衬砌相邻隧道中心水平线处土体初始超孔隙水压力为

式中：p0为前期固结压力；k0为土体静止土压力系数；M为临界状态线的斜率，对于上海土可取0.92。

图2 应力路径法确定超孔隙水压力[7]Fig.2 Excess pore water pressure determined by stress path method[7]

通过式（8）计算得到隧道中心水平线处的初始超孔隙水压力与式（1）计算得到的相应点的法向水土压力，可以得到相应的应力释放率，从而可以得到与衬砌相邻周边土体初始超孔隙水压力。

2.2 分布范围内任一点土体初始超孔隙水压力确定

2.2.1 初始超孔隙水压力分布范围确定

关于土体初始超孔隙水压力的分布范围，目前很少有学者研究。文献[16]给出了盾构施工引起的土体扰动范围计算方法，如图3所示的直线变化部分，图中r为隧道半径，r′为剪切扰动区半径，该法适合砂土。Mair等[17]通过离心试验研究表明，砂土和黏性土地层中隧道开挖面破坏形式表现不同，砂土地层中开挖面破坏形状表现为烟囱状，而在黏性土层中，由于土体颗粒间黏聚力的存在，破坏面表现为下部较缓、上部区域较大的盆状。即黏性土层中破裂面轮廓呈曲线。所以黏性土的实际扰动范围要比文献[16]提出的理论扰动范围大。

因此，笔者提出，黏性土中盾构施工引起的土体初始超孔隙水压力的分布范围（即实际扰动区域边缘）为一圆弧线（取隧道右半部分进行说明，如图3所示曲线ABC），曲线的A、C点可由文献[16]的研究成果来确定。由Mail[18]和Attewell[19]等推导的深层土体水平移动公式可知，隧道中心水平线处土体移动最大。笔者认为，B点为该边界线的中心点，可由隧道中心水平线的延长线与AC中垂线的交点来确定，得到这3点后即可确定曲线ABC。

若以地面为X轴，以向下并通过隧道轴心为Y轴，则该圆弧的A、B、C 3点及圆心O的坐标为A(0,h+r′)、C(w,0)、B(e,h)、O(x,y)。

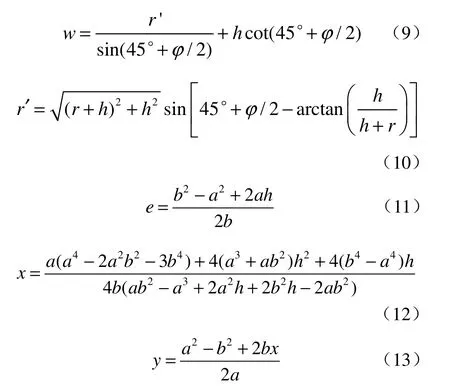
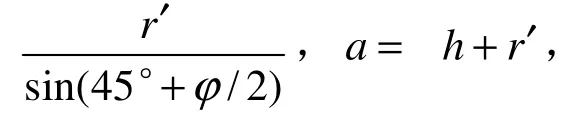
图3 盾构施工扰动分区Fig.3 Disturbance zone of shield tunnelling

2.2.2 任一点土体初始超孔隙水压力计算方法

本文运用文献[20]的应力传递理论对土体各点的初始超孔隙水压力进行了推导。假定：①侧面土体对土块的压力是均匀的；②土体内各点的初始超孔隙水压力是径向变化的，同时各点的初始超孔隙水压力值主要是由该处对应的与衬砌相邻土体初始超孔隙水压力U0传递的，不考虑其余处的U0对其的影响；③土块顶面处的土层受力U(Z)在一定深度处是均匀分布的，随径向距离不同而有所不同。

现取单位宽度1的土块初始超孔隙水压力的应力传递至某深度z处时的示意图如图4所示，公式推导如下：

图4 初始超孔隙水压力的应力传递Fig.4 Stress transfer of initial excess pore water pressure

（1）隧道拱顶上方土体：

对于侧面土压力U′的计算，取传至地表，此时地表的受力 U (0)=0，而土体保持平衡可知

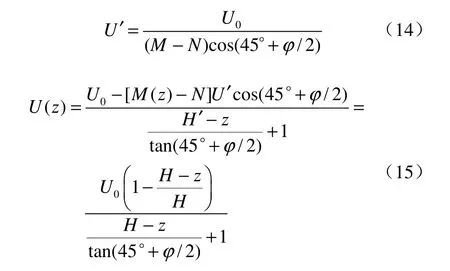
（2）其余处土体同理：

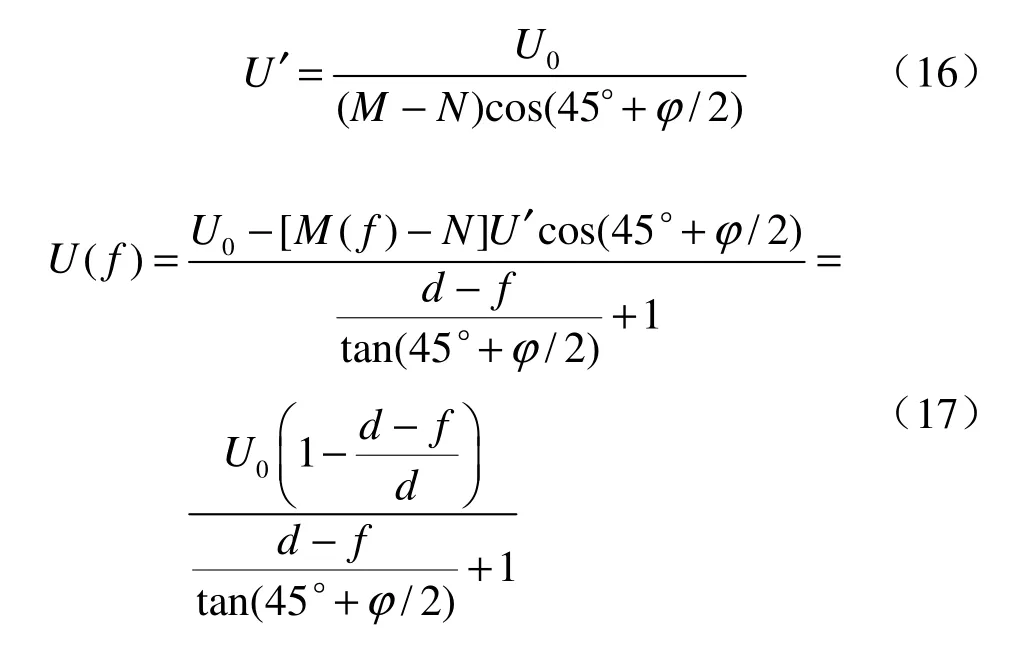
图5为运用本文方法与文献[2，5，21]的布置均为隧道顶部上方的孔压实测值进行比较。发现本文方法与实测值吻合，这表明实际所测得的孔压最大值即初始超孔隙水压力随着到衬砌的径向距离增大，其变化规律是呈凹曲线衰减的。同时文献[22]提出，盾构施工隧道周围土体受到施工扰动后，便在隧道周围形成超孔隙水压力区。一般盾构在推入某处地层后，盾构周围的超孔隙水压力的分布如图6(a)所示的状态。当盾构离开该处地层后，由于土体表面的应力释放，隧道周围的超孔隙水压力便下降，呈图6(b)所示的状态。

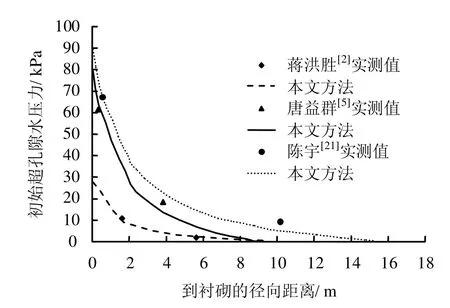
图5 初始超孔隙水压力实测值与计算值比较（单位：kPa）Fig.5 Comparison of calculated and observed initial excess pore water pressures (unit: kPa)

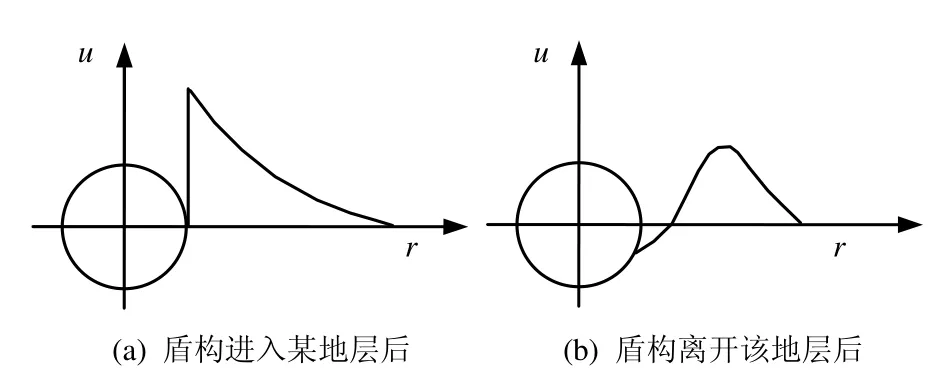
图6 超孔隙水压力分布图[22]Fig.6 Distributions of excess pore water pressure[22]

3 算例分析

现应用一个算例对本文理论进行解释说明。某盾构施工隧道所处土层为粉质黏土，土性与上海土相同，直径D=6 m，埋深h=12 m，黏聚力c=10 kPa，内摩擦角φ=20°，衬砌厚度t=350 mm，土体重度γ=18 kN/m3，地下水位1 m，土层抗力系数Ks=3000 kN/m3，土体损失率ε=2%。

3.1 与衬砌相邻的周边土体初始超孔隙水压力确定

由式（8）可知，隧道中心水平线临近点的初始超孔隙水压力为

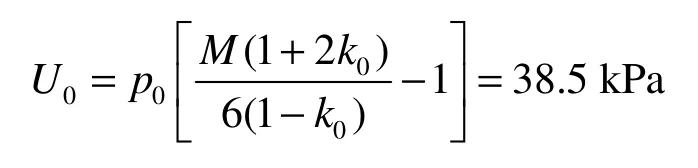
其中，p0为前期固结压力即隧道未开挖前的有效应力，p0=18×1+8×11=106 kPa；本文隧道所处土层为粉质黏土，与上海土质相似，取M=0.92[7]。

则可得到应力释放率：α=38.51/243.7=15.75%。

由式（1）～（4）可得与衬砌相邻的隧道周边土体法向围压，见图 7。在此基础上可得到与衬砌相邻的周边土体初始超孔隙水压力，见图 8。如图所示，土体初始超孔隙水压力分布是顶部小于隧道中心水平线处，其中最大的在隧道的底部，总体呈近似圆形（顶部小，底部大）。

图7 与衬砌相邻的隧道周边土体法向围压（单位：kPa）Fig.7 Confining pressures surrounding the tunnel lining(unit: kPa)

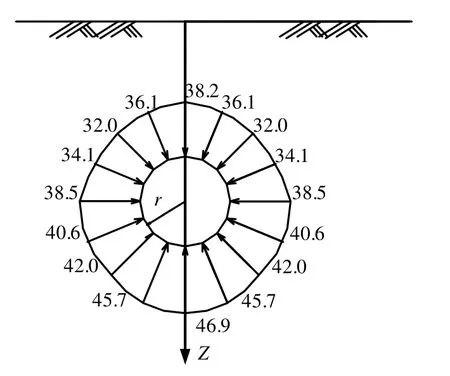
图8 与衬砌相邻的周边土体初始超孔隙水压力（单位：kPa）Fig.8 Distribution of initial excess pore water pressure surrounding the tunnel lining (unit: kPa)

3.2 土体任一点的初始超孔隙水压力确定

通过公式计算得到分布范围A、B、C及圆心O的坐标分别为 A(0,17.4)、B(11.3,12)、C(15,0)、O(-0 .5,1.8)，从而得到初始超孔隙水压力分布范围如图9所示。

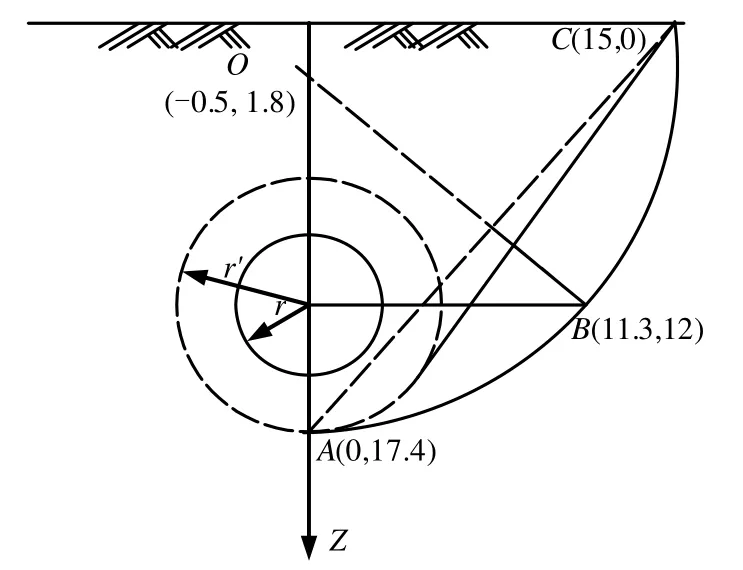
图9 隧道周边初始超孔隙水压力分布范围Fig.9 Distribution of initial excess pore water pressure surrounding the tunnel

由上述计算得到与衬砌相邻的隧道周边土体初始超孔隙水压力及分布范围，则可求出土体任一点的初始超孔隙水压力。现以隧道水平线处、隧道顶部及隧道底部为例进行说明，计算结果见图10。由图可知，随着离隧道中心距离的增加，隧道周边不同位置处的土体初始超孔隙水压力变化规律相近，都呈凹曲线形状衰减，最近点为最大；差别在于衰减的程度有所不同。对于隧道底部的土体，由于到临界点的距离很小，则其衰减最快。

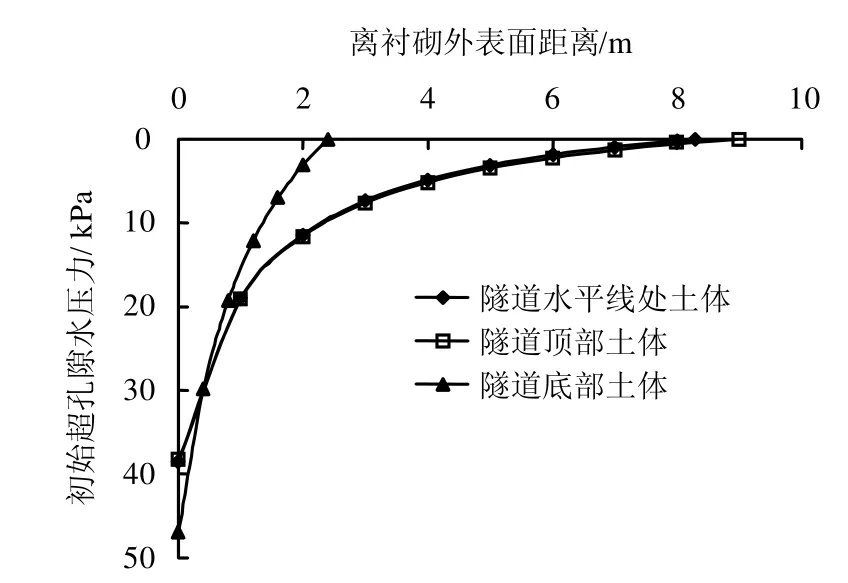
图10 土体初始超孔隙水压力分布Fig.10 Distributions of initial excess pore water pressure

图11为分布范围内土体初始超孔隙水压力等值线图，从图中可知，在隧道底部等值线较密，即变化快；而在隧道顶部一定范围内等值线间距逐渐变大，即衰减程度有所减缓。

图12为分布范围内土体初始超孔隙水压力在不同深度处的孔压分布。由图可知在隧道顶部上方土体，在不同深度处，土体初始超孔隙水压力以隧道轴线处为最大。且深度越大，其最大值也随之增大。并且在不同深度处的土体初始超孔隙水压力呈现出类似Peck曲线形状，这也解释了隧道工后沉降仍可用Peck曲线来拟合的缘由。

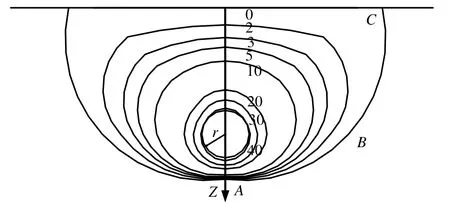
图11 初始超孔隙水压力等值线图（单位：kPa）Fig.11 Contours diagram of initial excess pore water pressure (unit: kPa）

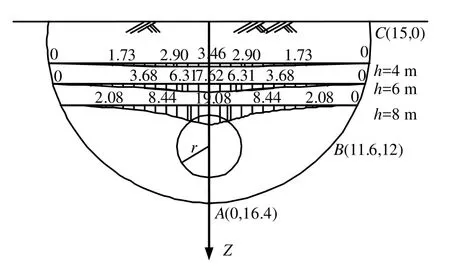
图12 土体初始超孔隙水压力随深度变化（单位：kPa）Fig.12 Initial excess pore pressure of soil with depth (unit: kPa)

4 结论及展望

（1）本文提出了盾尾通过后应力释放所形成的土体初始超孔隙水压力分布范围的确定方法，该分布范围随着隧道埋深的不同而有所不同，并与土性有关。

（2）运用应力释放理论，推导了与衬砌相邻的周边所有点的土体初始超孔隙水压力计算公式。在此基础上，对分布范围内任一点土体初始超孔隙水压力计算公式进行了推导。

（3）运用算例分析进行验证，结果表明：随着到隧道中心的距离的增加，土体各点的初始超孔隙水压力呈凹曲线衰减。不同部位处的衰减程度有所不同，隧道底部的土体比隧道水平及隧道顶部土体衰减得快。可以看出，隧道底部等值线最密，顶部一定范围内等值线间距逐渐增大。同时从不同深度处土体初始超孔隙水压力分布图可知，在隧道顶部上方土体，初始超孔隙水压力在一定深度处以隧道轴线处为最大，且呈现出类似Peck曲线，解释了隧道工后沉降仍可用Peck公式拟合的缘由。

由于该方法的研究尚处于初步阶段，仍有几个方面需进一步的研究：（1）鉴于目前有关超孔隙水压力监测数据的缺乏，未来需增加对隧道施工引起的超孔隙水压力的监测，以验证本计算方法的可靠性；（2）需考虑在衬砌周边不同的应力释放率情况下，计算盾构施工引起的周边土体初始超孔隙水压力。（3）盾构施工引起土体初始超孔隙水压力分布范围的确定将影响下一步推导结果的精确性，因此，需对其进行深一步的研究，使得本文计算方法完善。

[1]郑宜枫,丁志诚,戴仕敏. 超大直径盾构推进引起周围土体变形和土水压力变化分析[J]. 地下空间与工程学报,2006,2(8): 1349－1353,1378.ZHENG Yi-feng,DING Zhi-cheng,DAI Shi-min. An analysis of surrounding ground deformation and ground/water pressure fluctuations caused by a super large diameter TBM[J]. Chinese Journal of Underground Space and Engineering,2006,2(8): 1349－1353,1378.

[2]蒋洪胜,侯学渊. 盾构掘进对隧道周围土层扰动的理论与实测分析[J]. 岩石力学与工程学报,2003,22(9)：1514－1520.JIANG Hong-sheng,HOU Xue-yuan. Theoretical study and analysis of site observation on the influence of shield excavation on soft calys around tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2003,22(9): 1514－1520.

[3]易宏伟. 盾构施工对土体扰动与地层移动影响的研究[D].上海: 同济大学,1999.

[4]林志,朱合华,夏才初. 近间距双线大直径泥水盾构施工相互影响研究[J]. 岩土力学,2006,27(7): 1181－1186.LIN Zhi,ZHU He-hua,XIA Cai-chu. Study of field monitoring on interaction between twin slurry shield tunnels in close space[J]. Rock and Soil Mechanics,2006,27(7): 1181－1186.

[5]唐益群,张曦,王建秀,等. 粉性土中土压平衡盾构施工的扰动影响[J]. 同济大学学报(自然科学学报),2005,33(8): 1031－1035.TANG Yi-qun,ZHANG Xi,WANG Jian-xiu,et al. Earth pressure balance shield tunnelling-induced disturbance in silty soil[J]. Journal of Tongji University(Natural Science),2005,33(8): 1031－1035.

[6]魏纲. 盾构施工引起地面长期沉降的理论计算研究[J].岩石力学与工程学报,2008,27(增刊1): 2960－2966.WEI Gang. Research on theoretical calculation of long-term ground settlement caused by shield tunneling[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(Supp. 1): 2960－2966.

[7]张冬梅,黄宏伟,王箭明. 软土隧道地表长期沉降的黏弹性流变与固结耦合分析[J]. 岩石力学与工程学报,2003,22(增刊 1): 2359－2362.ZHANG Dong-mei,HUANG Hong-wei,WANG Jianming. Analysis of long-term settlements over tunnels using visco-elastic constitutive model coupled with consolidation theory[J]. Chinese Journal of Rock Mechanics and Engineering,2003,22(Supp.1): 2359－2362.

[8]徐方京,侯学渊,姜英. 软土盾构隧道的沉降分析[C]//中国土木工程学会隧道及地下工程学会第七届年会暨北京西单地铁车站工程学术讨论会论文集(下). 北京:[s. n.],1992: 446－449.

[9]徐方京. 软土中盾构隧道与深基坑开挖的孔隙水压力与地层移动分析[D]. 上海: 同济大学,1991.

[10]SKEMPTON A W. The pore pressure coefficients A and B[J]. Geotechnique,1954,4(4): 225－262.

[11]HENKEL D J. The shear strength of saturated remoulded clays[C]//Proceedings of Research Conference on Shear Strength of Cohesive Soils. Boulder,Colorado: ASCE,1960: 533－560.

[12]孙瑞锋. 城市地下管道非开挖技术的岩土力学研究[D].重庆: 重庆大学,2005.

[13]夏明耀,曾进伦. 地下工程设计施工手册[M]. 北京:中国建筑工业出版社,1997.

[14]朱伟,胡如军,钟小春. 几种盾构隧道管片设计方法的比较[J]. 地下空间,2003,23(4): 352－356.ZHU Wei,HU Ru-jun,ZHONG Xiao-chun. Comparative study of several segment design methods for shield tunnels[J]. Underground Space,2003,23(4): 352－356.

[15]孙钧. 地下工程设计理论与实践[M]. 上海: 上海科学技术出版社,1996.

[16]魏纲,魏新江,龚慈,等. 软土中盾构法隧道引起的土体移动计算研究[J]. 岩土力学,2006,27(6): 995－999.WEI Gang,WEI Xin-jiang,GONG Ci,et al. Study of calculation for shield tunneling-induced ground movements in clays[J]. Rock and Soil Mechanics,2006,27(6): 995－999.

[17]MAIR R J,TAYLOR R N. Theme lecture: Bored tunnelling in the urban environment[C]//Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering. Hamburg: Balkema,1997: 2353－2385.

[18]MAIR R J,TAYLOR R N,BRACEGIRDLE A.Subsurface settlement profiles above tunnels in clays[J].Geotechnique,1993,43(2): 315－320.

[19]ATTEWELL P B,YEATES J,SELBY A R. Soil movements induced by tunneling and their effects on pipelines and structures[M]. London: Blackie,1986.

[20]代志宏,吴恒,张信贵. 附加应力在土体中传递分布的细观模型[J]. 工程地质学报,2004,12(增刊): 73－78.DAI Zhi-hong,WU Heng,ZHANG Xin-gui. The mesoscopic structure model of additional stress transfer in the soil[J]. Journal of Engineering Geology,2004,12(Supp.): 73－78.

[21]陈宇,朱继文. 双圆盾构隧道的流固耦合分析[J]. 地下空间与工程学报,2010,6(1): 21－27,101.CHEN Yu,ZHU Ji-wen. Coupled fluid-mechanical analysis of DOT shield tunnel[J]. Chinese Journal of Underground Space and Engineering,2010,6(1): 21－27,101.

[22]刘建航,侯学渊. 盾构法隧道[M]. 北京: 中国铁道出版社,1991: 330－333.