飞机舱门密封结构的气密可靠性研究

刘 伟，刘志群，赵晓博，席宝安，岳珠峰

（西北工业大学 力学与土木建筑学院，西安710129）

飞机舱门密封结构的气密可靠性研究

刘 伟，刘志群，赵晓博，席宝安，岳珠峰

（西北工业大学 力学与土木建筑学院，西安710129）

采用可靠性思想分析飞机舱门密封结构参数对密封性能的影响。对两种型号的舱门密封带进行整体规格的压缩实验，拟合成Ogden模型代入有限元计算获得门体与门框的二次接触力的隐式响应关系。将关门行程、装配尺寸、挡件尺寸等视为随机变量，采用Monte Carlo法对两种密封带的气密可靠性进行比较，得到了密封结构参数的均值灵敏度和方差灵敏度，对舱门密封带选型与结构的优化设计提供参考。

舱门密封结构；密封带；气密可靠性；灵敏度

飞机舱门的密封是防止舱内漏气或失压的重要保障［1］，气密性能与密封结构的设计密切相关。图1是某型飞机舱门组合密封结构截面示意图，它主要由P型密封带、密封压条、Z型挡件、门体和门框组成。图中的d1为门体与门框间隙；d2为挡件纵向距离；d3为Z型挡件横向尺寸；d4为关门行程；r为档件导角半径。但是，由于制造误差、安装同轴度以及使用过程中的磨损等因素，将导致密封结构的实际位置与设计值存在随机偏差，这种离散性威胁着舱门的气密可靠性。

密封带是一种能够发生大变形的高弹性橡胶材料［2］，其压缩变形特性对舱门整体的气密刚度起主导作用，是选型的重要依据之一。已经有很多学者利用有限元分析方法分析了实心橡胶圈的压缩应力特性［3－5］，研究对象涉及指尖密封、O型密封，球型密封等。在密封材料性能、仿真以及结构参数对密封性能的影响分析方面进行了十分有益的尝试［6－9］。本工作选取目前飞机舱门中应用较为广泛的P型密封带组合密封结构，考虑了密封结构参数的随机性，基于密封带压缩实验结合有限元仿真，采用Monte Carlo法抽样分析了密封结构气密可靠性和参数灵敏度。

图1 舱门密封结构截面示意图Fig.1 Constructed profile of aero－port seal structure

1 密封带压缩实验

1.1 实验件与实验方法

舱门密封带实验件如图2所示，其尺寸为660mm×1360mm，内径为10mm，P型截面，硬度值（邵氏）为50。实验测试的两种密封带分别为：①平纹型织物增强，厚度1.5mm；②普通橡胶型（无织物增强），厚度2mm，实验测试压缩量均为0～7mm。

图2 密封带实验件实物图Fig.2 The test specimen of sealing trip

根据实验件的尺寸及加载类型，选用FTS复杂加载系统1＃动作器进行实验（量程：10kN，±60mm）。实验装夹示意图如图3所示，将密封圈实验件固定在平板舱门模拟件的卡槽上，平面门体与油缸连接，通过实验机作动筒的伸缩来控制压缩量，底部采用配对的平面门框承压件来模拟关门后的门框。作动筒加载速率设置为0.2mm／s，可视为静态加载。实验加载平板舱门压头稍大于密封圈，尺寸为700mm×1400mm，为保证平板的加载刚度，平板舱门压头材料为45号钢，厚度为20mm。实验前首先对FTS设备的测试力进行标定，以消除夹具重力影响，同时利用水平仪对加载夹具进行水平校核。

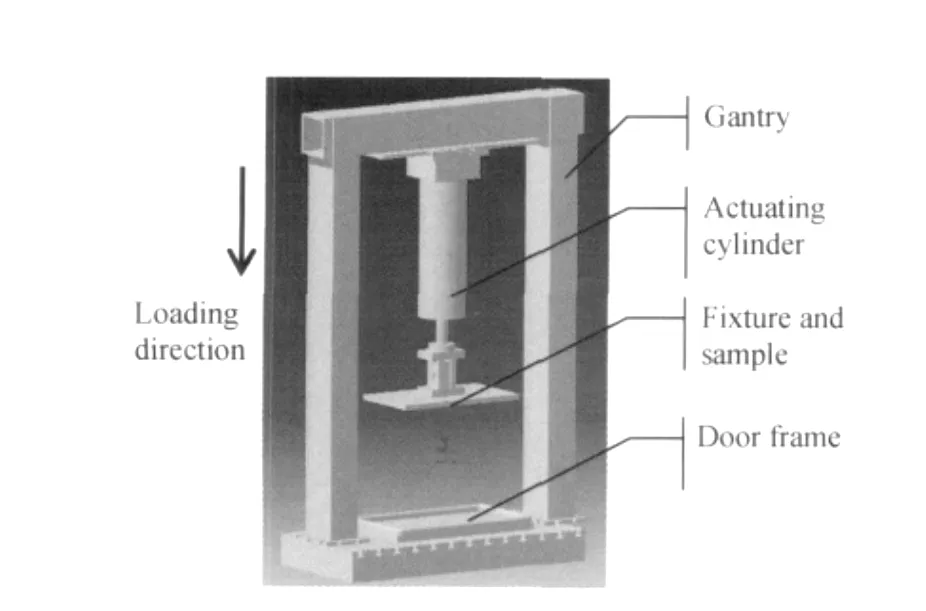
图3 密封带压缩实验装夹示意图Fig.3 The schematic diagram of clamping and loading for compression tests

1.2 实验结果

实验过程中测量并记录密封带的压缩量，每增大1mm记录对应的加载力值，实验结果如图4所示。可见，压缩力随着压缩量呈非线性上升趋势，并且在相同变形量下，织物增强型密封带的压缩力明显高于普通橡胶密封带，具有更大的压缩比。

图4 两种型号密封带的载荷－变形实验测试曲线Fig.4 Experimental compressive force－displacement curves of two type sealing strips

2 确定性分析

2.1 有限元模型

相比飞机舱门门体、门框和挡件材料（E＝70GPa），密封圈材料的模量很小（E＝0.0075GPa），密封带作为大柔度结构直接决定着门体的气密刚度，需要着重关注密封带的变形。因此，将门体、门框、密封压条和挡件近似为刚体，只考虑密封带的变形。建立舱门密封结构的有限元模型，如图5所示，单元类型选择四节点平面应变Herrmann单元，单元总数为650。

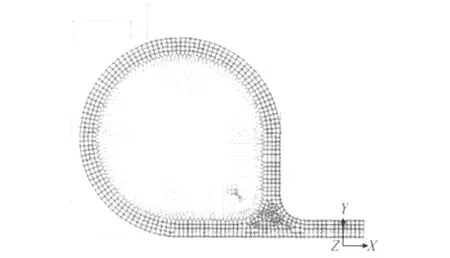
图5 飞机舱门密封结构的有限元模型Fig.5 FEM analysis model of aero－port seal structure

飞机舱门密封带一般设计有小孔，飞行过程中舱内压力能够通过这些眼孔渗透进入密封圈内，不但起到了加强密封的作用，还能够延长密封圈使用寿命。圈内气压的作用效果可以采用MARC软件中特有的CAVITY（气囊空穴模型）单元来模拟。正常飞行条件下，舱内保压恒压值设定为0.076MPa。摩擦模型为库仑模型，硬铝与橡胶的摩擦因数取0.25。

2.2 密封带材料模型

密封圈是橡胶材料，工程上较常采用 Mooney－Rivlin模型，或者Ogden模型来描述该材料特性。利用MSC.Marc软件中的“Evaluate Material”功能分别采用上述两种模型对密封圈压缩实验数据进行拟合，发现Ogden模型与实验数据基本吻合（图6），在单轴拉压中，Ogden模型在超大应变时也具有良好的符合性，能够较好地适应非常数的剪切模量情形和材料的轻微压缩行为，已被成功地应用于密封圈和其他橡胶工业产品分析。其应变能函数定义为：

式中：W为应变能密度分别为3个主应力方向上的伸长率；N一般取3；μk，αk为模型系数，可以通过拟合实验应力－应变数据得到。

图6 采用Ogden模型拟合密封圈材料实验数据Fig.6 Experimental data fit of Ogden model for seal

2.3 仿真结果分析

舱门关闭过程中，密封圈是一个大变形、大应变过程，其有限元网格不断发生移动、扭曲，尤其是与刚体界面（门框和挡板）相接近的单元经常在接触与非接触之间变动，采用MARC对接触区域的自适应网格重划分技术，解决网格畸变问题，可以获得更为精确的结果。图7为采用接触区域网格自适应加密计算得到的密封带截面Cauchy应力分布情况，最大应力出现在密封圈与挡件的接触部位，大小约15.5MPa。

密封圈与门框和Z型挡件的单位面积接触力与关门行程的关系如图8所示。图中X－frame表示密封带与门框的X方向接触力，X－baffle，Y－baffle表示密封带与档件的X方向和Y方向的接触力（X，Y的方向如图5所示）。由图8可知，当关门压缩量达到1.73mm，密封圈首先与Z型挡件发生接触；当关门压缩量达到3.95mm时，密封圈与门框发生接触，是二次接触。在接触点，接触力与关门量是折线关系（连续但不可导）。随着关门量增大，由于克服摩擦接触面产生微小滑移，计算过程中接触力显示会发生小幅跳动，显然接触力与舱门密封结构参数密切相关。

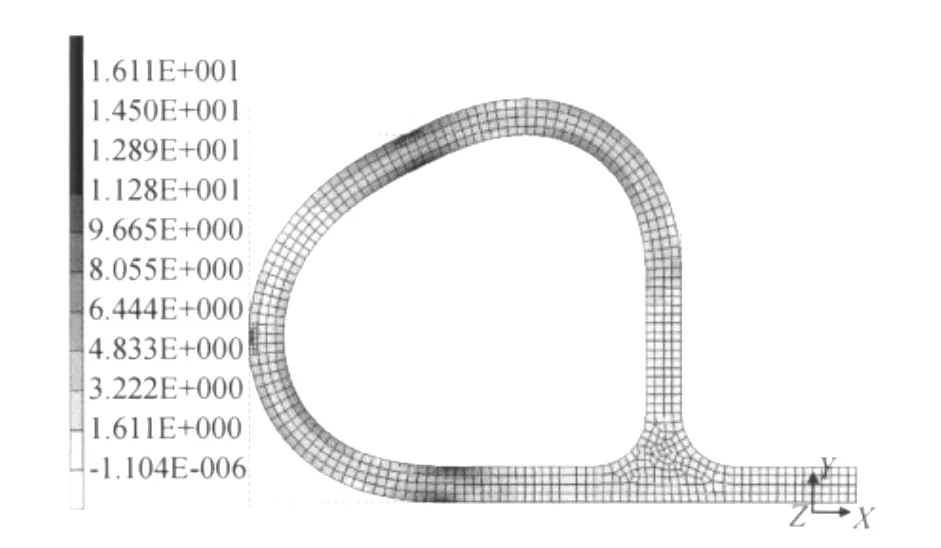
图7 舱门关闭时密封圈的Cauchy应力及接触区域网格重划分Fig.7 Contacting－remesh and Cauchy stress of sealing strip when the aero－port closed

图8 单位面积接触力与关门行程的关系Fig.8 The relation between the contact force per area and closing－stroke

3 可靠性分析

3.1 随机变量与极限状态函数

由于制造误差、安装偏差或者使用过程中门轴等的磨损，均将导致实际装配尺寸与设计理想值发生随机偏差，使密封圈的压缩接触力不能够达到密封要求。这里着重评估上述变量对舱门密封带密封性，根据概率论中心极限定理，一般可认为结构尺寸服从3σ（σ为标准差）的均值正态分布，且相互独立。随机变量及其分布特征如表1所示。

密封失效是可靠性评估中的一项重要失效模式。密封带通过发生弹性变形填满相互接触的门体、门框表面之间的间隙，并维持一定的接触压力，从而达到气密效果。泄露率是定量评估舱门密封效果的重要指标，泄露经常是由于密封压缩力不足导致的，因此接触力常常作为密封结构气密性的评判指标［5，8］，舱门设计要求能够承受3倍设计压差载荷的内外压差，折算到单位接触面积上的压缩力要求大于0.25N，因此密封失效的极限状态方程gi可以定义为：

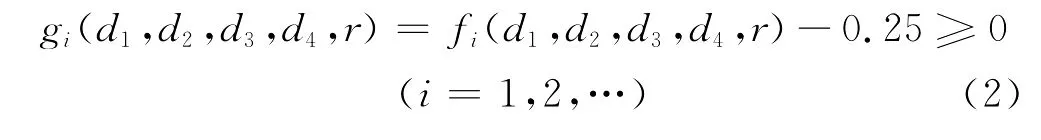
表1 随机变量及其分布特征Table 1 The parameters of seal structure and distribution characteristics

式中：fi（＊）为门体与门框的二次接触力，与舱门密封结构参数密切相关，其隐式响应关系可以通过有限元确定性计算获得，i为抽样次数。根据应力－强度干涉原理，式（2）小于零时的次数与总计算次数的比值即为密封结构的失效概率。

3.2 可靠性分析方法及过程

采用Monte Carlo法进行可靠性计算，主要基于以下3点：（1）密封结构计算涉及接触问题，其压缩响应具有非线性隐式关系，对于隐式极限状态方程的可靠性分析，Monte Calro法计算思路简单且易于编程实现；（2）由上述确定性分析可知，密封圈与门框属于二次接触问题，结构参数不但决定了接触力的大小，还决定了能否发生接触，不发生接触时接触力恒为零，因此，密封圈与门框之间接触力与结构参数之间的响应关系是一个接触点位置随机变化并且与密封圈与挡件的第一次接触相关，会导致难以拟合合适的响应面和计算收敛性问题［10］；（3）Monte Carlo法的结果可信度要高于其他方法，常常作为校核其他方法的依据。本密封圈单次确定性仿真的时长较短，因此Monte Carlo法的计算成本仍然在可接受的范围。

结合自编程实现数据指定分布的随机化处理与抽样，同时调用 Marc软件进行上述确定性计算，计算完成后提取密封带与门体的接触力进行失效统计并代入可靠度计算公式和灵敏度公式，获得舱门密封结构的失效概率和各个随机参数的灵敏度。分析流程如图9所示。

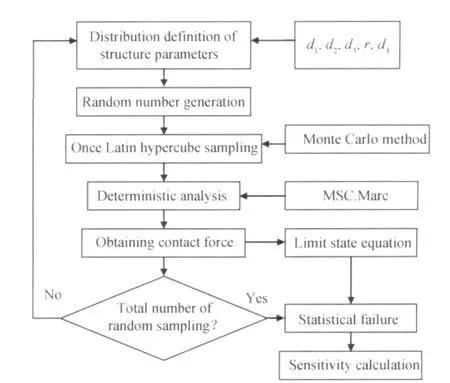
图9 采用Monte Carlo法分析舱门密封结构气密可靠性流程图Fig.9 Air－tight reliability analysis process of aero－port seal structure by Monte Carlo method

3.3 可靠性分析结果

采用Monte Carlo法对随机样本进行抽样5000次，分别计算得到两种密封圈的失效概率对比，如表2所示，Pr为抽样计算获得的可靠度。两者敏度分析结果大致一致，织物增强型密封带由于较好的压缩比具有更高的密封可靠度。

表2 两种密封带的气密可靠度及其概率敏度分析结果Table 2 The reliability，mean value sensitivity and variance sensitivity results for two types sealing strips

织物型密封带的密封组件主要结构变量的均值灵敏度和方差灵敏度分析结果如图10所示，可见合理减小门框间距d1，挡件纵向距离d2和挡件导角半径r，增大Z型挡件横向尺寸d3和关门压缩量d4，均有助于提高气密可靠性。这些变量中，d1，d2，d4的均值和r的方差对失效较为敏感，设计和生产、维修检验过程中需要严格这些尺寸的检查。

另外，设计过程中还应注意上述随机变量对舱门其他性能的双面影响，例如：（1）d1太小会使密封带被挤出或“碰框磨框”影响关门便利性和增大磨损；（2）减小d2或增大d4虽然能够增大接触应力，但是会直接加重开关门手柄力度，在保证气密性的前提下设计合适的关门压缩率是至关重要的；（3）增大d3会减小舱门有效面积，甚至可能会与开关门连杆机构发生干涉；（4）增大r会导致密封带的应力集中，削弱其使用寿命。所以设计过程中还应在保证密封的基础上，综合考虑上述因素和性能指标要求，从而制定出合理的设计范围。

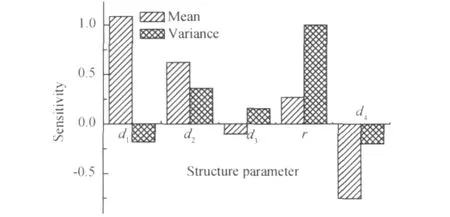
图10 密封结构随机变量灵敏度分析结果（织物型密封带）Fig.10 The sensitivity results of seal structure parameters（fabric sealing strip）

4 结论

（1）设计过程中在保证密封可靠性的基础上，须综合考虑参数的两面性，结合性能指标要求制定合理的设计范围。

（2）织物型密封带具有更高的压缩比，比非织物型密封带具有更高的气密可靠度，建议优先选用。

（3）装配尺寸（门框间距、挡件纵向间距）和关门行程量的均值和挡件导角半径的方差对失效较为敏感，设计和装配、维修检验过程中需要严格这些尺寸的检查。

［1］ 飞机设计手册总编委会.飞机设计手册（第十册）［M］.北京：航空工业出版社，2003.

［2］ 李晓芳，杨晓翔.橡胶材料的超弹性本构模型［J］.弹性体，2005，15（1）：50－58.

［3］ 王伟，赵树高.橡胶O形密封圈的接触变形及应力分析［J］.弹性体，2005，15（4）：28－31.

［4］ 孙兵晓，常新龙，胡成荣，等.固体火箭发动机密封结构随机有限元可靠性分析［J］.火箭推进，2008，34（5）：22－26.

［5］ 常洁，陈同祥.航天器中一种典型O形密封圈的有限元分析［J］.航天器工程，2008，17（4）：104－108.

［6］ 任全彬，蔡体敏，胡春波.固体火箭发动机密封结构设计参数分析［J］.弹箭与制导学报，2006，26（3）：151－157.

［7］ 王红艳，陈国定，张延超.指尖密封性能与结构参数的灵敏度分析［J］.润滑与密封，2008，33（10）：11－14.

［8］ 王建军，高新陵.O形橡胶密封圈尺寸公差对密封性能的影响［J］.机电产品开发与创新，2008，21（5）：79－80.

［9］ 刘纪涛，张为华.基于Kriging模型的密封圈非概率可靠性分析［J］.润滑与密封，2010，35（1）：67－70.

［10］ 吕震宙，宋述芳，李洪双，等.结构机构可靠性及可靠性灵敏度分析［M］.北京：科学出版社，2009.

Air－tight Reliability Analysis of Aero－port Seal Structure

LIU Wei，LIU Zhi－qun，ZHAO Xiao－bo，XI Bao－an，YUE Zhu－feng
（School of Mechanics and Civil.＆ Architecture，Northwestern Polytechnical University，Xi’an 710129，China）

The reliability method was applied to analyze the influence of the seal structure parameters on the air－tight performance of aero－port.The Ogden constitutive model was fitted based on compression experimental data of two types of aero－port sealing strip，which was applied to simulate the implicit response of secondary contact force between the door body and door frame by FEM.The seal structure’s parameters such as closing－stroke，assembly dimension，and baffle sizeetcwere treated as random variables，the reliability of the two sealing strips types was compared by Monte Carlo method.The mean value sensitivity and variance sensitivity of above parameters were obtained.The results were helpful for the sealing strip selection and seal structure optimum design.

aero－port seal structure；sealing strip；air－tight reliability；sensitivity

TH114

A

1001－4381（2012）04－0047－05

科工技技术基础资助项目（Z142010B001）；高等学校学科创新引智计划资助项目（B07050）

2011－04－06；

2011－11－12

刘伟（1981－），男，博士，讲师，主要从事结构疲劳和可靠性方面的研究，联系地址：西北工业大学长安校区883信箱（710129），E－mail：lw＿npu＠mail.nwpu.edu.cn