欧氏群与二次曲线方程的化简

尹彦彬， 王建永， 陈敏茹

（河南大学数学院，开封 475004）

欧氏群与二次曲线方程的化简

尹彦彬， 王建永， 陈敏茹

（河南大学数学院，开封 475004）

讨论欧氏群E（2）在二次曲线方程化简理论中的应用.在此背景下，给出二次方程化简的方法；讨论了二次曲线方程的若干性质.

欧氏群；反射；二次曲线

1 预备知识

在本文中我们约定coli（A）表示A的第i列向量；At表示A的转置；向量u的单位化记为u0.考虑二次曲线Γ的一般方程

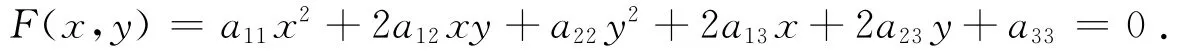
为了方便起见，特引进一些记号

定义1.1［1］二次曲线的一族平行弦的中点轨迹是一条直线，这条直线称为二次曲线的共轭于平行弦方向的直径.

定义1.2［1］设l为二次曲线的一条直径，如果它垂直于自己的共轭弦，则l称为主直径，主直径的方向和垂直于主直径的方向称为主方向.

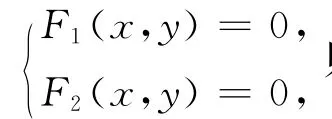
命题1.2二次曲线的主直径的共轭方向是A2的非零特征根对应的特征向量的方向.

证 设X∶Y为主直径弦的方向，主直径方向为X′∶Y′，则有X′∶Y′＝－Y∶X.由命题1.1，X′∶Y′＝－（a12X＋a22Y）∶（a11X＋a12Y）＝－Y∶X，得

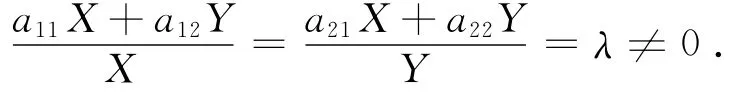
从而X∶Y为A2的属于非零特征根λ的特征向量.

（i）有心二次曲线（detA2≠0）：此时二次曲线有唯一中心（x0，y0）.A2有两个非零特征根，所以二次曲线有两个主方向.设X∶Y为一主方向，则其共轭方向为－Y∶X，也是主方向.那么以X∶Y为主方向的主直径为YF1（x，y）－XF2（x，y）＝0，另一主直径方程为XF1（x，y）＋YF2（x，y）＝0.当然它们经过二次曲线中心（x0，y0），所以以X∶Y为主方向的主直径可以表示为

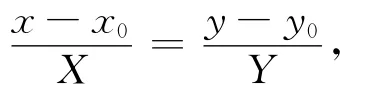
参数方程表示为

2 二次曲线的化简

2.1 欧氏群.

定义2.1平面上的运动群

平面上的运动是三种运动合成的即沿任意给定向量的平移，旋转某个角度和关于过原点直线的反射.后两种构成正交群O（2，R）.

说明 （i）旋转某个角度的变换即将原来的向量逆时针旋转θ角度，对应变换

这里detR＝1矩阵R对应的旋转变换记为fR，即fR（x，y）＝（x，y）Rt.

（ii）关于直线y＝tanθx反射，对应变换

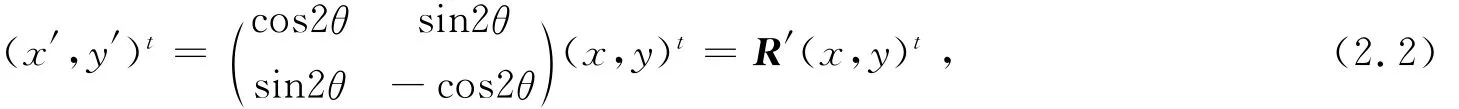
这里detR′＝－1.矩阵R′对应的反射变换记为fR′，即fR′（x，y）＝（x，y）R′t.

（iii）沿向量a＝（a1，a2）的平移，（x′，y′）＝（x＋a1，y＋a2）.向量a对应的平移变换记作Ta，即Ta（x，y）＝（x，y）＋a.

Rn空间到自身的等距群称为Rn上的欧氏群［2］，记作E（n）.任意的欧氏变换能被分解为正交变换和平移的复合.因此，E（n）可以表示为E（n）＝｛（x，R）｜x∈Rn，R∈O（n，R）｝对应欧氏变换记作f（a，R）＝Ta◦fR即f（a，R）（x，y）＝（x，y）Rt＋a.容易看出，平面上的欧氏群就是运动群M（R2）.

说明E（n）不是一般线性群GL（n，R）的李子群，而且平移不满足线性.但是存在同构

使得E（n）成为GL（n＋1，R）的李子群［2］.由此视为矩阵李群.于是在E（n）中的乘积、取逆定义如下：

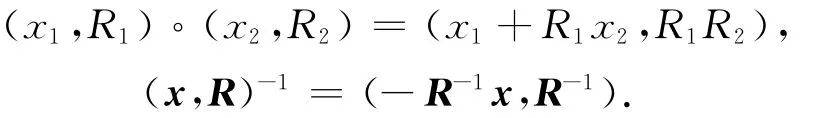
命题2.1Ta＝f（a，I）和fR＝f（0，R）.

2.2 二次曲线化简.

设（a，R）∈E（2），对应欧氏变换（x′，y′）＝f（a，R）（x，y），则有（x′，y′，1）t＝（a，R）（x，y，1）t.

推论2.1在平移变换Ta下，A′2＝A2和F′3＝（F1（a），F2（a），F（a））t.

推论2.2对有中心的二次曲线，取a为二次曲线的中心时，在平移变换Ta下，一次项系数F1（a）＝F2（a）＝0.在正交变换下，设R∈O（n，R），

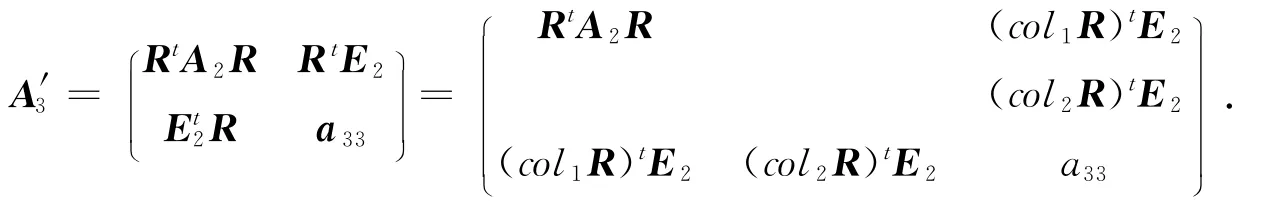
推论2.3在正交变换fR下，A′2＝RtA2R和

命题2.2［3］存在平面上的正交变换R，使得A2化为对角型，即RtAR＝Λ＝diag（λ1，λ2），其中λ1，λ2为A2的特征根，R的列向量col1R，col2R为属于λ1，λ2单位正交特征向量.

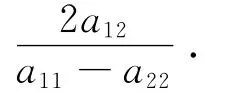
推论2.5设u＝（x1，x2）t为属于λ的单位特征向量，那么（x1，x2）A2（x1，x2）t＝λ.

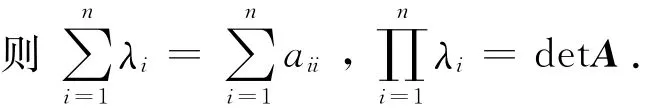
推论2.6设A2的特征根为λ，μ，则（x1，x2）是属于λ的特征向量，那么（－x2，x1）为属于μ的特征向量.

命题2.3给定二次曲线F（x，y）＝（x，y，1）A3（x，y，1）t，行列式I1，detA2，detA3在平移、旋转和反射变换下不变，称为二次曲线的不变量.

证根据特征方程和上述定理我们可以得到I′1＝trA′2＝trA2＝I1.对于detA2是显然的，因为detA′2＝det（RtA2R）＝detA2.考虑det（a，R）＝1.因此，

其中前一式为共轭于u2的直径，即主直径.从而a为抛物线的顶点.

［1］吕林根，许子道， 解析几何［M］.4版.高等教育出版社，2007.

［2］Brian C.Hall，Lie groups，Lie algebras，and representations，an elementary introduction［M］.世界图书出版社.

［3］王萼芳，石生明.高等代数［M］.3版.北京：高等教育出版社，2007.

Euclidean Groups and the Simplification of Conic Equations

YINYan－Bin，WANGJian－Yong，CHENMin－Ru
（School of Mathematics and Information Sciences，Henan University，Kaifeng 475004，China）

This paper is an application of the Euclidean groupE（2）to the simplification of Conic equations.In this way，we provide a method of the simplification of conic equations and discuss some properties of conic.

Euclidean group；reflection；conic

O182

A

1672－1454（2012）04－0107－06

2010－03－26