水位下降条件下黏性土边坡稳定性的图表法

年廷凯，刘 成，万少石，张克利

（1.大连理工大学 土木水利学院，辽宁 大连 116024；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；4.大连九成测绘信息有限公司，辽宁 大连 116400）

1 引 言

对于库（河）岸边坡与堤坝、高填方路堤边坡、人工开挖边坡等边坡工程，经常由于坡体迎水面水位的下降造成坡体局部或整体稳定性降低，导致滑坡现象发生。对于工程人员来讲，如何快速评估水位变化条件下的边坡稳定安全系数显得至关重要。国内外许多学者采用各类解析与数值方法获得了大量的不同表达形式的边坡稳定性图表，给地质或岩土工程师快速评估边坡的安全性提供了有力参考。其中Taylor[1]在1937年首先应用土坡稳定分析摩擦圆法得到了不考虑孔隙水压力的边坡稳定性图表法；Morgenstern[2]应用条分法，通过简化土体内部的孔隙水压力，得到了水位骤降条件下土质边坡稳定性的图表；Desai[3]假定水位下降率与土体的渗透系数比为定值情况下，应用有限元法获得了骤降条件下坡体稳定性的图表；Cousins[4]采用孔隙水压力比获得了坡体内部的孔压，通过极限平衡法获得了简单土质边坡的稳定性图表；Viratjandr等[5]通过应用极限分析上限方法，将影响土坡稳定性的参数进行分类整合，通过简化处理土坡内的孔隙水压力，建议了 4种不同水位下降模式下的边坡稳定性图表；万少石[6]通过有限元渗流计算，获得土坡内不同时刻的渗流场，再结合强度折减法求解边坡稳定性系数，并采用图表方式对变动参数条件下的边坡稳定性进行了初步研究。

纵观现有图表法，大多不考虑坡体内部的孔隙水压力或采用简化的孔压比，或对浸润线做简化处理，不能考虑坡外库（河）水下降与坡内浸润线变化的联动效应；在稳定性方面，只考虑边坡坡角、水位下降比、土性参数或综合土性参数的影响，很难做到全面考虑。本文在文献[6]研究的基础上，采用非稳定渗流有限元法，合理模拟库（河）水位变化引起的坡体内孔隙水压力变化，将土坡内不同时刻的渗流场与应力变形场结合分析，并将影响边坡稳定性的主要参数进行分类整合，采用强度折减技术获得不同参数组合下考虑水位下降过程的边坡安全系数；针对一般黏性土边坡，提出边坡相对安全系数的综合图表方法。

2 有限元计算理论

2.1 静力平衡方程

将整个土体分为土骨架和孔隙水，其中孔隙水不可压缩，则考虑静水压力的多孔介质静力平衡方程以张量形式表达如下[7]：

式中：σij,i为有效正应力；σf,j为孔隙水压力；Fj为单位体力。

2.2 连续性方程

采用达西定律计算流-固耦合问题，同性多孔介质材料固结下的渗流方程表达式[8]为

式中：εvol为体应变；pf为孔隙水压力；n′为孔隙率；β′为孔隙水的压缩模量；k为渗透系数；γw为水的重度；t为时间。其中渗透系数k并非常数，它与饱和度和孔隙率密切相关，通常可用描述土-水特征曲线和非饱和透水系数的拟合公式模型表达[8－9]。有关公式如下：

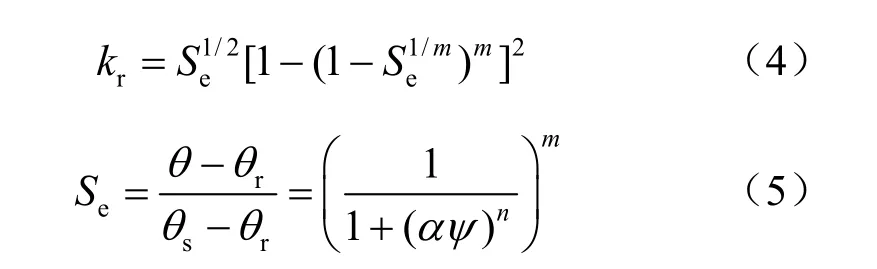
式中：Se为相对饱和度；θs与θr为最大、最小体积含水率；ψ为负压水头； m=1-1/n；α、n为土的非饱和参数；kr为相对渗透系数；kw为饱和渗透系数。

2.3 有限元数值实施

应用ABAQUS程序进行强度折减有限元计算，首先在渗流分析中引入土-水特征曲线、相对渗透系数与饱和度关系曲线，通过对现有程序的二次开发，采用VF6.5对土坡迎水面的边界条件进行改进，使水位可随着时间变化，合理模拟非饱和-非稳定渗流，从而获得不同时刻、不同水位条件下土坡内的渗流场及真实的浸润线分布。在稳定性分析中，不考虑自由水面以上负孔隙水压力（基质吸力）的影响，将负孔隙水压力简化为 0。以有限元数值计算不收敛并综合考虑坡体等效塑性应变带贯通作为边坡失稳判据，将边坡内不同时刻的渗流场与应力变形场结合分析，获得各水位变化条件下的边坡稳定安全系数。

3 非稳定渗流条件下土坡稳定性分析

3.1 参数的选取原则

水位变化条件下边坡稳定性的主要影响因素为坡度、坡高，坡外水位下降比、下降速率、边界透水状况、边坡土体渗透系数、给水度、内摩擦角和黏聚力及土-水特征曲线等。如若单一的考虑各个因素，在数值计算及后期图表处理上都会遇到很大的困难，这里对主要参数进行分类整合、综合表达。主要组合参数为水位下降比L/ H，坡角β，相对降速比k/μV，无量纲参数λ=c/γHtan φ等。其中无量纲参数λ[5,10]，源于探讨一定坡角条件下，参数F/tanφ与 cd/γ H tanφd的关系，cd和φd是折减后的强度参数，具体如式（6）所示。

这种表达式的优点在于参数λ与安全系数F相对独立，并且涵盖坡体的基本土性参数，大大简化了图表参数的表达形式。

相对降速比k/Vμ选做判别库（河）水位降落快慢的一个组合指标，其中k为土体的渗透系数，μ为土体的给水度，V为库（河）水位的下降速率。考虑到黏性土渗透系数的区间范围和一般库（河）水位下降速率的大小，本文选取的参数k/Vμ值大致包括了所研究的黏性土的合理比值区间。渗透系数k取值范围为 1× 10-4～ 1× 10-6cm/s ；结合文献[11]，黏性土的给水度变化区间较小，取μ=0.02；水位下降速率V取值范围为0.1～10 m/d。利用有限元程序进行验证，当参数k/μV取值相同时，不同参数组合下能够得到相同的渗流场。因此，计算中取相对降速比k/μV来评判水位下降快慢是可行的。

为了更好地模拟实际涉水边坡边界透水状态，采用两种不同边界条件，一种考虑两侧面均不透水，另一种考虑一侧透水，一侧不透水边界条件。

关于土-水特征曲线，针对一般黏性土岸坡，选用一组典型的 VG 模型土-水特征参数[9]，其中α=1.06 m-1，n=1.395，θr=0.106，θs=0.469；通过式（3）与式（5）的拟合可得到如图1所示的土-水特征曲线、相对渗透系数与饱和度的关系曲线。

图1 典型的黏性土-水特征曲线Fig.1 Typical soil-water characteristic curves for clay

3.2 模型的建立

考虑边坡的一般性，取文献[6]边坡作为算例，其坡体几何尺寸与材料参数如下：坡高H=10 m，重度γTot=20 kN/m3，变形参数为弹性模量E=100 MPa，泊松比ν=0.3。边坡底面为不透水边界条件，侧面分为前述的两种情况考虑。边坡底面采用完全约束条件，左右采用水平约束条件。土体本构模型采用 Mohr-Coulomb破坏准则与非相关联流动法则的理想弹塑性模型，单元形式采用四边形二次单元。

3.3 参数的影响

3.3.1 λ=c /γ Htan φ对边坡稳定安全系数的影响

为了考查参数λ对边坡稳定性的影响，选取λ分别为 0.025(c=2 kPa ，φ=21.8°)、0.05(c=3.64 kPa，φ=20°)、0.1(c=7.28 kPa ，φ=20°)、0.2(c=14.56 kPa ，φ=20°)、0.4(c=29.12 kPa ，φ=20°)、0.8(c=58.24 kPa ，φ=20°) 6种比值下的边坡相对安全系数。如图2，绘制了15°、30°、45°3种坡角情况下，不同水位下降比边坡相对安全系数。

图2 不同坡角和不同水位下降比情况下F/tanφ -λ关系曲线Fig.2 The relative FOS of slope under different slope angles and water level drawdown ratios

分析图2可见，曲线呈现上凸趋势，在同一水位下降比条件下，相对安全系数F/tanφ随着c/γ H tan φ值的增大而增大。这是因为边坡的稳定性主要受土体本身的强度参数影响，内摩擦角和黏聚力的大小直接影响了最终的坡体稳定性。对于单一参数，边坡安全系数F随着黏聚力的增大而增大，对于内摩擦角也有相同的结论。

3.3.2 相对降速比k/Vμ对边坡安全系数的影响

为了研究参数k/Vμ对边坡稳定安全系数的影响，图3分别绘制了β=30°边坡水位下降条件下k/μV分别为0.1、1.0、10、100，4种比值情况下的相对安全系数，λ分别选取0.05、0.1、0.4、0.8，4种土性参数下，相对安全系数与水位下降比的变化关系。

图3 不同λ和不同相对比值情况下F/tanφ -L/H关系曲线Fig.3 The relative FOS under different values of λ and k/μV

从图3可以看出，在同一下降比条件下，参数k/μV越大，相对安全系数也就越大；当参数λ较小时，相对安全系数随k/Vμ的变化波动较大；随着λ的不断增大，变化幅度趋于稳定。当参数λ=0.05，k/Vμ从0.1增加到100时，相对安全系数的增幅最大可达35.8%；当参数λ分别等于0.1、0.4、0.8时，相对安全系数的最大增幅分别为28.4%、10.2%和8.06%。这表明随着土体自身强度的增加，水位变化对坡体的安全系数的影响也在不断的减弱。

从以上的分析结果可以看出，k/Vμ较小时，土体渗透系数小，而水位下降速率快，从而导致坡体排水时间短，孔隙水压力不能很好地消散，坡体内渗流自由面在库水位降落后仍然保持很高的位置，导致坡体内外的水压力差加大，从而降低了坡体的安全系数；k/Vμ较大时，则恰恰相反。当k/μV相当小时，趋近于0时，坡体内自由面在水位下降过程中接近于不动，属于极限状态时的骤降，不利于坡体本身的安全；相反，当k/Vμ越大，趋近于无穷大时，自由面下降速度几乎与坡体外侧的库（河）水位下降速度相同，这时属于缓降状态，有利于边坡体安全。

3.3.3 边界条件对边坡安全系数的影响

选取相对降速比k/Vμ的不同比值，获得各值下土坡内最终浸润线位置。研究结果表明，k/Vμ能够合理反映边坡在水位下降条件下，从缓降到骤降整个过程中浸润线的变化情况。为了考查边界透水条件对边坡稳定安全系数的影响，选取β=30°边坡、两种透水边界条件进行分析。相应边界条件下的相对安全系数结果如图4所示。从图中可以得到，同一边坡在两种不同透水边界条件下，坡体相对安全系数结果差别不大。经过计算，在k/Vμ情况下，不透水边界改为透水边界后，相对安全系数最大降幅为7.4%；在k/Vμ==100情况下，不透水边界改为透水边界后，相对安全系数最大降幅为9.57%，随着参数λ的不断减小，边界的透水条件对稳定安全系数的影响将有所增加。因此，在有限元数值计算中，应尽可能根据实际情况选取不同的边界透水条件。

4 边坡稳定性的图表法

以无量纲参数 λ=c/γ Htan φ反映基本土性、以相对降速比k/Vμ反映岩土渗透特性，分别建立不同坡角β（15°，30°，45°）边坡在水位下降条件下相对稳定安全系数F/tanφ与无量纲参数λ、相对降速比k/Vμ、水位下降比L/ H的相关关系，得到一系列图表，其中部分图表如图5所示。对于实际工程，可根据获得的大量图表直接查得或采用插值方法获得边坡稳定的安全系数。

图4 不同λ和k/μV情况下F/tanφ -L/H关系曲线Fig.4 The relative FOS under different values of λ and k/μV

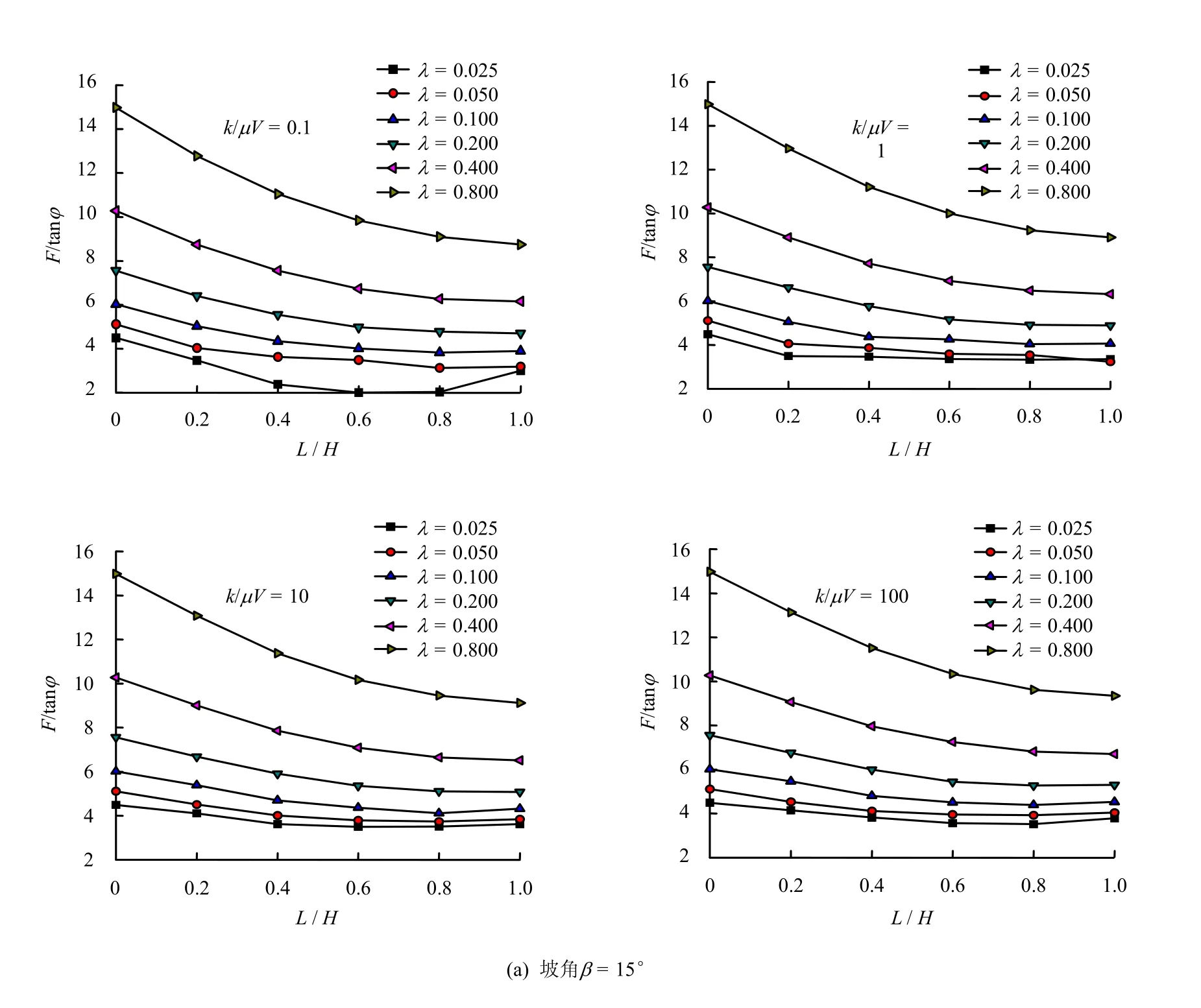
图5 边坡稳定性图表Fig.5 Slope stability charts

5 对比分析及验证

为了考察强度折减有限元法分析库水位变化情况下边坡稳定性的适用性及其稳定性，本节选取图表法中的1条曲线与极限平衡法进行对比分析。选取图表法中图5(b)，坡角β=30°，k/Vμ=1.0，λ=0.4，（c=29.12 kPa，φ=20°）曲线，与边坡工程分析软件GEO-SLOPE的计算结果进行对比分析，计算结果如图6所示。

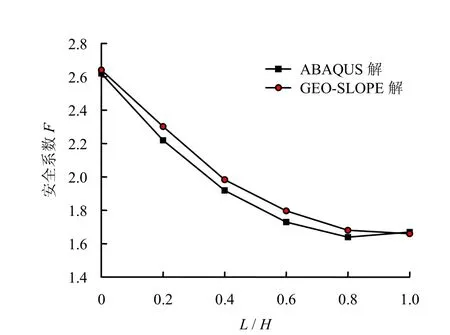
图6 计算结果对比分析Fig.6 Contrast of the computed results

由图可见，强度折减有限元法的计算结果与GEO-SLOPE极限平衡法的计算结果比较接近，最大偏差仅为3.7%。由此可见，采用ABAQUS程序进行水位下降条件下的边坡稳定性分析是合理可行的。

6 实例分析

利用绘制的大量图表，在实际工程中可根据边坡的土性参数及水位下降条件直接查得不同工况下的边坡稳定安全系数；另外，图表法还可应用于库（河）岸边坡的工程设计中，根据水位条件、土质特性、设计安全性要求等来设计库岸与河堤坡度。以下列举一例进行说明。

某涉水边坡土性参数如下：c′/γH=0.0728，内摩擦角φ′=20°，k/Vμ=1.0，边坡设计安全系数要求Fs=1.2，考虑水位变化的影响，给出边坡坡比的合理取值范围。

根据参数λ与k/Vμ的比值大小，通过查阅图表，获得在不同下降比条件下，边坡稳定安全系数与坡角余切值cotβ的关系曲线，如图7(a)所示。当边坡设计安全系数取Fs=1.2时，可以得到不同下降比时最大坡比曲线，如图7(b)所示。分析曲线发现，库（河）水位变化L/ H=0～1.0区间时，最不利水位大体位于L/ H=0.8附近，对于水位变化条件下的边坡稳定性而言，这是一个最小稳定安全系数水位值，与文献[12－13]已有研究结论是一致的，这里取坡比(H: L)为3:1可以满足任意下降比条件下边坡稳定要求。

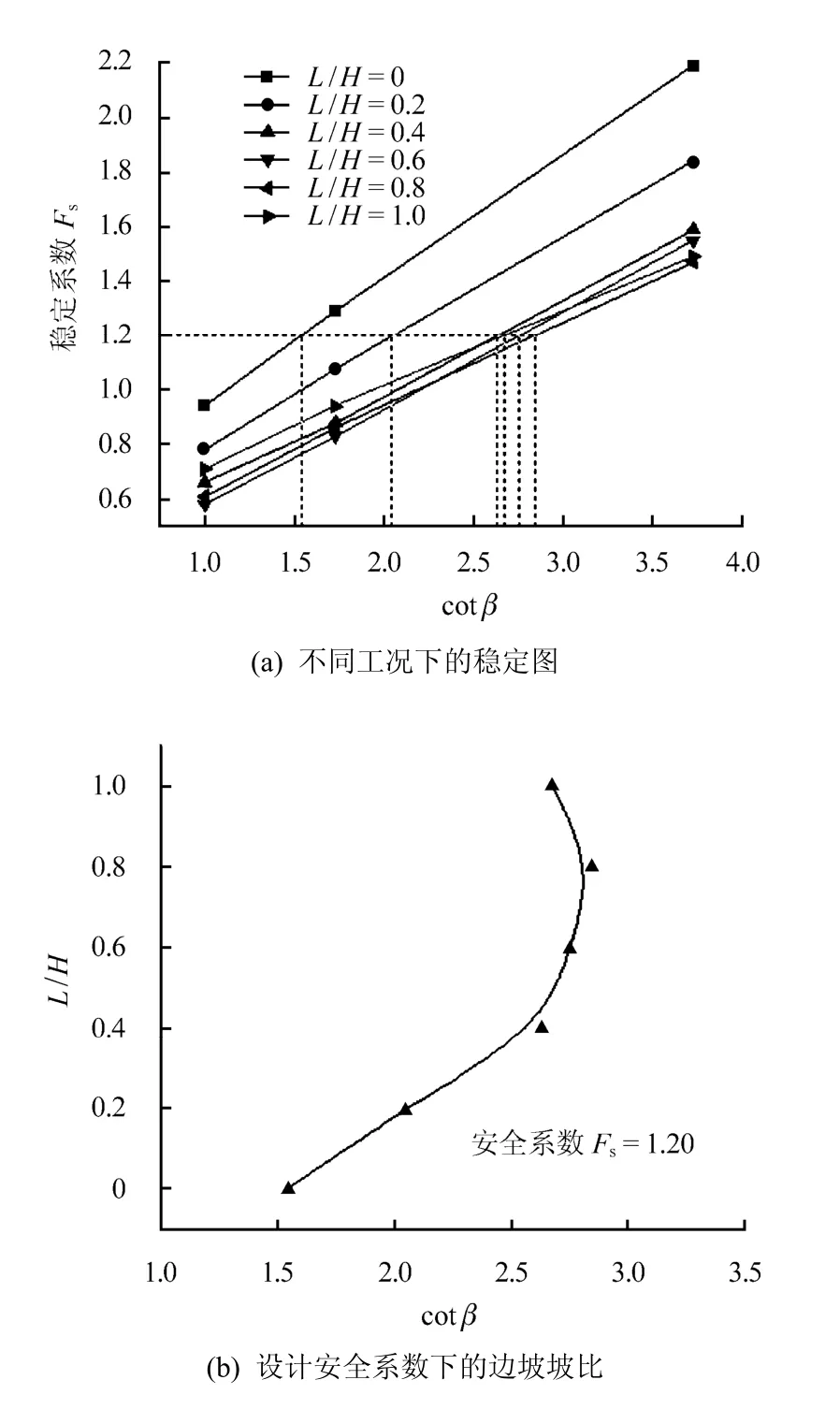
图7 图表法应用实例Fig.7 Application of graphic method

7 结论与建议

（1）在同一水位下降比条件下，相对安全系数F /tanφ随着无量纲土性参数λ值的增大而增大，随着相对比值k/Vμ的增大而增大。

（2）当无量纲土性参数λ值较小时，相对安全系数F/tanφ随相对比值k/Vμ的变化波动幅度较大；随着λ值的不断增大，库（河）水位变化对相对安全系数F/tanφ的影响不断减弱。相对比值k/μV可用于合理评价水位下降条件下边坡稳定性。

（3）在数值计算中，应根据边坡工程的实际情况选取不同的边界透水条件，一般情况下边界透水条件对边坡稳定安全系数的影响不大。

（4）综合考虑边坡稳定的各类影响因素，提出水位下降条件下黏性土边坡稳定性的图表方法，通过实例分析验证，本文方法可行。为快速评估中小型库（河）岸边坡和堤坝在水位变化条件下的稳定性提供了直接依据，是对现行图表法的有益补充。

本文所研究提出的边坡稳定安全系数综合图表表示方法，在现阶段仍局限于边界简单、地质条件相对均匀的土质边坡，更复杂的情况有待于深入研究。

[1] TAYLOR D W. Stability of earth slopes[J]. Journal of the Boston Society of Civil Engineers, 1937, 24(3): 337－386.

[2] MORGENSTERN N. Stability charts for earth slopes during rapid drawdown[J]. Geotechnique, 1963, 13(2):121－131.

[3] DESAI C S. Drawdown analysis of slopes by numerical method[J]. Journal of the Geotechnical Engineering Division, 1977, 103(7): 667－676.

[4] COUSINS B F. Stability charts for simple earth slope[J].Journal of the Geotechnical Engineering Division,1978, 104(2): 267－279.

[5] VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown[J].Canadian Geotechnical Journal, 2006, 43(8): 802－814.

[6] 万少石. 涉水边坡稳定性的三维强度折减有限元分析[硕士学位论文D]. 大连: 大连理工大学, 2009.

[7] 钱家欢, 殷宗泽. 土工原理与计算(第二版)[M]. 北京:中国水利水电出版社, 1996

[8] UGAI K. A method of calculation of total factor of slopes by elasto-plastic FEM[J]. Soils and Foundations, 1989,29(2): 190－195.

[9] VAN GENUCHTEN MTH. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Sci. Am. J., 1980, 44(5): 892－898.

[10] BELL J M. Dimemsionless parameters for homogeneous earth slopes[J]. Journal of the Soil Mechanics and Foundations Division, ASCE,1966, 92: 51－65.

[11] 张蔚榛, 张瑜芳. 土壤的给水度和自由空隙率[J]. 灌溉排水学报, 1983, 3(2): 1－16 ZHANG Wei-zhen, ZHANG Yu- fang. Specific yield and free voidage of the soil[J]. Journal of Irrigation and Drainage, 1983, 3(2): 1－16.

[12] 马崇武, 刘忠玉, 苗天德, 等. 江河水位升降对堤岸稳定性的影响[J]. 兰州大学学报(自然科学版), 2000,36(3): 56－60.MA Chong-wu, LIU Zhong-yu, MIAO Tian-de, et al. The influence of water level changing on the stability of river embankment[J]. Journal of Lanzhou University (Natural Sciences), 2000, 36(3): 56－60.

[13] 年廷凯, 万少石, 蒋景彩, 等. 库水位下降过程中土坡稳定强度折减有限元分析[J]. 岩土力学, 2010, 31(7):2264－2269.NIAN Ting-kai, WAN Shao-shi, JIANG Jing-cai, et al.Finite element analysis(FEA) of slope stability by strength reduction technique under drawdown conditions[J]. Rock and Soil Mechanics, 2010, 31(7):2264－2269.