客观世界的n元关系——兼谈传统形式逻辑和数理逻辑

龚启荣

(贵州大学，贵阳 550025)

客观世界的n元关系
——兼谈传统形式逻辑和数理逻辑

龚启荣

(贵州大学，贵阳 550025)

当代形式逻辑对客观世界n元关系的研究，其视野是传统形式逻辑和数理逻辑无法相比的。从主导思想上看，传统形式逻辑是真正的名副其实的逻辑科学，但它只研究1元关系，不研究多元关系和真正普遍有效的关系推理，因此，传统形式逻辑顶多只能算n分之1的逻辑。数理逻辑虽然把1元或多元关系作为自己的研究对象之一，但它没有从内涵的角度去区分关于同一外延的k个尽管相当然而并不相同的n元关系，从量上说至少是“挂1漏k－1”的，即只从外延的角度研究一种关系而漏掉(k－1)种关系，因此，纯外延的数理逻辑顶多只能算k分之1的逻辑。当代形式逻辑从研究论域上的n目组和n目组集入手，亦即通过确定论域上的个体的所有不同序列，对论域上n个个体(n≥1)之间的所有关系进行了逻辑科学应有的全方位研究。

当代形式逻辑;传统形式逻辑;数理逻辑;n目组;n目组集;n元关系

古希腊亚里士多德2300多年前开创的传统形式逻辑的推理能出新知、论证不许循环、深深植根于同自然语言紧密联系的人的普通逻辑思维实际等思想，迄今久盛不衰。但是，传统形式逻辑演算技巧陈旧简陋，因而发展缓慢。数理逻辑虽然系统地采用清晰的符号语言，演算技巧精密严格，但它把非函数的以充分条件为核心的真正的逻辑关系处理成同语反复的真值函数和个体－真值函数关系，完全背离了传统形式逻辑深刻正确的主导思想，彻底离开了逻辑科学的发展轨道，成为一门离散的基础数学(又称“真值数学”或“二值数学”)。我们的研究立足于辩证唯物论，充分肯定先贤韩非自发的客体逻辑倾向，以自觉的逻辑客体说为主导思想，坚持传统形式逻辑真正的逻辑科学方向，继承其久盛不衰的理论成果，尽力廓清笼罩在它身上朦胧的历史迷雾，在不背离其主导思想从而不会发展成为数学的一部分的先决条件下，借鉴现代数学精确的演算方法，探讨具有当代科学水准的客体说当代形式逻辑。当代形式逻辑就是应用按照指谓同一准则同自然语言相互翻译的符号语言的机械的排列和变形方式去探讨以客观世界事件之间的客观的充分条件关系为核心的逻辑结构和逻辑规律，从而向人们提供认识和改造客观世界的普遍有效的从已有知识获取新知识的工具。

当代形式逻辑对客观世界n元关系的研究，其视野是传统形式逻辑和数理逻辑无法相比的。当代形式逻辑从讨论论域上的n目组和n目组集入手，亦即通过确定论域上的个体的所有不同序列，对论域上n个个体(n≥1)之间的所有关系进行了逻辑科学应有的全面分析。因此，为了讨论清楚n元关系，我们得先讨论n目组和n目组集。

一、n目组和n目组集

(一)论域上的n目组

讨论所涉及的不空的个体的领域称为论域，以U加撇或下标表示。譬如，数学研究现实世界的数量关系和空间形式，而生物学则以生物为探讨的对象领域。对于所进行的讨论来说，论域是最广泛的集，讨论只在这个范围内进行。关于对象的讨论不仅需要有作为分析的起点的对它进行分解的个体，而且还需要有作为概括的终点的始终不可逾越的论域。

若e1、e2、…、ei、…、en是论域U中的n(n为非负整数)个未必互异的个体，则由之组成的具有一定顺序的排列(简称序列)称为U上的一个有序n目组，简称为n目组。论域U上的n目组可表示为:

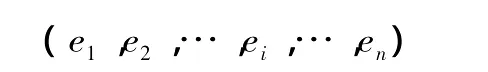
左右括弧表示n目组的起止范围，括号中的e1、e2、…、ei、…、en表示组成该n目组的U中的n个未必互异的个体序列。

“屈原是伟大的诗人”这句话指谓的事实涉及到的个体域是“人”，故，其论域是“人”，而(屈原)便是“人”这个论域上的一个1目组。“越南入侵柬埔寨”这句话指谓的事实涉及到的个体域是“国家”，其论域是“国家”，而(越南，柬埔寨)便是“国家”这个论域上的一个2目组。“地球内邻金星外邻火星”这句话指谓的事实涉及到的个体域是“太阳系”，其论域是“太阳系”，而(地球，金星，火星)便是“太阳系”这个论域上的一个3目组。可见，当讨论客观上存在着某一个事实时，就可以确定这个事实所涉及到的不空的领域，即论域，同时也可以确定这个确实有的论域上的n目组。

在序列的n个位置中，任意两个不同位置上出现的个体未必互异，其意思是说，在n目组中，任意两个个体ei和ej可以不同，但也可以相同。

论域U上的全部n目组，是这个论域内的个体的全部可能的不同序列。鉴于在序列的n个位置中的任意两个不同位置上出现的个体未必互异，因而，在序列中出现的互异的个体数可以小于n，当然可以等于n，但是不会大于n;序列中不同的位置有且仅有n个。正由于此，我们称含有n个不同位置的序列为“n目组”，而不称“n元组”。比如，任意一首7言律诗，除去题跋，共有56个汉字，这首7言律诗就是论域“汉文字”上的一个56目组，而其中互不相同的汉字就是这56目组的互不相同的个体，这些互不相同的个体不会多于56个，可以等于56个，可以少于56个(如果这首7言律诗中有重复的汉字)，但这56目组的目有且仅有56个。

(二)n目组的性质

与论域上的n元子集不同，论域U上的n目组的性质主要有:

1.个体排列的有序性

n目组中个体的排列是有次序的，换一下顺序就会改变原n目组的性质，成为新的n目组;而n元子集与构成该集的n个元的排列顺序无关(n元子集的元具有无序性)，改变元的排列顺序仍然是同一个n元子集。例如，(2，1，3)和(1，2，3)是论域“自然数”上两个不同的3目组，前者满足关系“…介于…和…之间”，后者却不满足;而{2，1，3}和{1，2，3}是论域“自然数”上同一个3元子集，因为它们的元相同，无需排列顺序。又如，(地球，太阳)和(太阳，地球)是太阳系的两个不同的2目组，前者满足关系“…绕…转”，不满足关系“…比…大”，但后者满足“…比…大”，而不满足“…绕…转”。然而，{地球，太阳}和{太阳，地球}则是太阳系的同一个2元子集，因为它们的元相同，也无需排列顺序。

2.个体可重复性

在n元子集中，任一属于该集的元只能在这个集中出现一次，这就是集中之元的单一性。然而，对于同一个n目组来讲，n个位置中出现的个体未必不同，或者说，n目组中可以有重复出现的个体。例如，(3，3)和(3)不同，前者是论域“自然数”上的一个2目组，满足2元关系“…与…相等”，后者则是论域上的一个1目组，满足1元关系“…是奇数”;{3，3}和{3}是论域“自然数”上的同一个子集，只是{3，3}表述不规范。(雷锋，螺丝钉)和(雷锋，雷锋，螺丝钉)不同，一个是2目组，一个是3目组，前者满足2元关系“…像…”，后者满足3元关系“…把…比作…”;{雷锋，螺丝钉}和{雷锋，雷锋，螺丝钉}是同一个集，只是{雷锋，雷锋，螺丝钉}表述不规范。

3.当论域的基数为m时，U上的n目组的数目可以大于m，而n元子集的元的个数不可能大于m

以“英文字母”为论域，由于互不相同的英文字母共有26个，故这个论域的基数是26。一首出现200个字母的英文诗就是这个26元论域U上的一个200目组，它的目数远远大于U的基数，而该26元论域的n元子集的元的个数绝不会大于26。

(三)n目组的种类

对论域U上的n目组进行分类，可按“目”的有无，先把n目组分为空组和实组，然后再按“目”的数量分为1目组和多目组，即:

当n目组的n＞0时，该n目组就叫实组。在实组中，当n=1时称为1目组;当n＞1时称为多目组。当n=2时，除了称为2目组外，有时也称为“序偶”、“序对”或者称为“有序偶”、“有序对”。

以“太阳系”为论域，(金星)就是这个论域上的一个1目组，(金星，水星)就是这个论域上的一个2目组，(金星，水星，地球)就是这个论域上的一个3目组，这3个n目组中目的个数大于0，因而都称为实组。

当n目组中目的个数等于0，即n=0时，该n目组就叫0目组，又称为空组。在空组中，其目数为0，也就是论域中的任何个体不会在其中出现。空组可用中空的括弧“()”表示。这个中空的括弧表明在其中没有位置，因而也没有个体。空组并不是不满足任何性质，而是切切实实地满足“不存在”，而且只有空组才满足这个性质，因为任何目数大于0的n目组都必须满足性质“存在”，不会满足“不存在”。比如说“美国历史上的皇帝是女的”，这显然是以“人”为论域，但在人这个论域中，“美国历史上的皇帝”是空组，因为美国历史上根本就没有皇帝。

(四)m元论域上的n目组的个数

1.相同的n目组和不同的n目组

同一论域上的两个n目组(e1，e2，…，ei，…，en)、(e'1，e'2，…，e'i，…，e'n)，若它们的每一对ei和e'i(1≤i≤n)均相同，则这两个n目组是相同的n目组。若其中至少有一对ei和e'i不相同，则这两个n目组是不相同的n目组。(北京，天津，上海，苏州)与(北京，天津，上海，西安)就是“城市”这一论域上两个不同的4目组，因为它们有一对个体“苏州”、“西安”不同。

2.m元论域上的n目组的个数

由于论域U上的全部n目组(n指确定的一个非负整数)是这个论域内的个体的全部可能的不同序列，因此，m元论域上的全部n目组应该是m元论域内的m个个体的全部不同的序列。一般说来，m元论域上的不同的n目组共有mn个。

(五)论域U上的n目组集

由且仅由U上的任意n目组为元组成的集，称为论域U上的n目组集(n为确定的非负整数)。更通俗地说，论域U上的n目组集就是以论域上所有具有相同目数的n目组为元组成的集合。以“人”为论域，满足1元关系“…是歌唱演员”的1目组有:(关牧村)、(李谷一)、(董文华)、(殷秀梅)、(德德玛)、(陈美玲)、(费翔)等等。以所有这些1目组为元构成的集{…(关牧村)，(李谷一)，(董文华)，(殷秀梅)，(德德玛)，(陈美玲)，(费翔)，…}，就是论域“人”上的一个1目组集。仍以“人”为论域，满足2元关系“…早于…”的2目组有(孔子，孟子)，(老子，庄子)，(施惠，公孙龙)，(董仲舒，杨雄)，(王充，王弼)，…。以所有这些2目组为元构成的集{…(孔子，孟子)，(老子，庄子)，(施惠，公孙龙)，(董仲舒，杨雄)，(王充，王弼)，…}就是论域“人”上的一个2目组集。

论域U上的n目组集可用符号Un表示(n为目数)，U0、U1、U2、U3、U4、U5就分别表示U上的 0目组集、1目组集、2目组集、3目组集、4目组集、5目组集。按照n目组集的定义，采用一般元刻划法，n目组集可表示为:

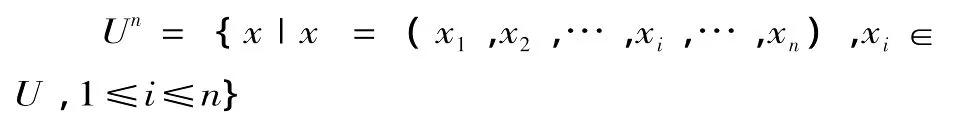
其中，(x1，x2，…，xi，…，xn)表示论域U上的任一n目组。

由于n目组集是以论域U上的任意n目组为元组成的集，并且m元论域U上不同的n目组共有mn个，因此，m元论域U上n目组集的元的个数就为mn个。或者说，当U的基数为m时，不同的n目组共有mn个，因此，m元论域U上n目组集的基数就为mn。亦即，m元论域U上的n目组集Un为mn元集。

二、n元关系

一个论域的n目组集确定了这个论域的个体的所有可能的序列。在这个基础上我们就可以进一步讨论论域U上某个个体或n个个体之间的所有可能关系，即n元关系。

(一)n元关系的定义

若集P的任意元均为集Q的元，则称P为Q的子集，以P⊂Q(读做“P含于Q”)表示。若P⊂Q且QP，则称P为Q的真子集。

若P⊂Un(集P为n目组集Un的一个子集)，且p为P的共仅属性，则称p为U上的一个n元关系。较通俗地说，U上的一个n元关系p就是U上的n目组集的一个子集P的共仅属性。

例如，论域U为 4元集{(a)，(b)，(c)，(d)}，集Q1={(a，a)，(b，b)，(c，c)，(d，d)}，Q1是论域U上的2目组集U2的一个子集，用q1表示“…等于…”，q1就是集Q1的共仅属性，这个共仅属性q1就称为U上的一个2元关系。论域U2为{x|x是人}，通俗地说，以人为论域，集P={…，(赵高，胡亥，李斯)，(秦桧，赵构，岳飞)，(魏忠贤，朱由校，周顺昌)，…}，是论域U上的3目组集U32的一个子集，其的共仅属性p是“…通过…杀害…”，这个共仅属性p就称为U32上的一个3元关系。而“…侵略…”则是论域“国家”上的一个2元关系，它是U22的下述这个确定的2元子集的共仅属性:{…，(美国，中国)，(日本，中国)，(德国，苏联)，(英国，阿根廷)，…}。

若n元关系的n=1，则这样的n元关系就称为1元关系。如，论域U2为{x|x是人}，集R={…，(李斯)，(岳飞)，(周顺昌)，(赵高)，(秦桧)，(魏忠贤)，(奥巴马)，(布什)，(卡特)，…}，R是论域U2上的1目组集U12的一个子集，它的共仅属性r是“…是人”，这个共仅属性r就称为U2上的一个1元关系。又如，集S={…，(鲁迅)，(巴金)，(郭沫若)，(但丁)，(歌德)，(高尔基)，(巴尔扎克)，(李白)，(杜甫)，…}，S是论域{x|x是人}上的1目组集U12的一个子集，它的共仅属性s是“…是文学家”，这个共仅属性s就称为论域{x|x是人}上的一个1元关系。

(二)m元论域U上不同的n元关系

1.互相对当的不同的n元关系

我们知道，任一集的共仅属性未必是唯一的。当论域U上的n目组集Un的任一子集P具有一个以上互相对当的共仅属性p1、p2、…、pi、…、pk时，这k个互相对当的共仅属性又称为论域U上互相对当的不同的n元关系。比如，论域U={x|x是人}上的1目组集U1的一个子集P为{(马克思)，(恩格斯)}，这个子集就有两个互相对当的共仅属性:p1为“…是科学社会主义的创始人”，p2为“…是《共产党宣言》的作者”，p1和p2就是论域{x|x是人}上的2个互相对当的1元关系。又如以太阳系为论域，太阳系这个论域上的2目组集的一个子集Q为{(月亮，地球)，(地球，太阳)}，集Q有两个互相对当的共仅属性:q1是“…绕…转”，q2为“…比…小”，q1和q2就是论域太阳系上的2个互相对当的2元关系。

2.互不相当的n元关系

一个n元关系pi也就是论域U上的n目组集Un的幂集P(Un)的一个元(即Un的一个子集)的共仅属性，而P(Un)的不同的元作为Un的一个子集，具有不同的共仅属性p1、p2、…、pi、…、pk。这些不同的共仅属性不仅互不相同，而且互不相当，因此称为论域U上的互不相当的n元关系。

当论域U的基数为m时，论域U上的n目组集Un的基数为mn，此时，Un的不同的子集共有2mn。以4元论域(即基数m=4)为例，4元论域上3元关系的个数就为:

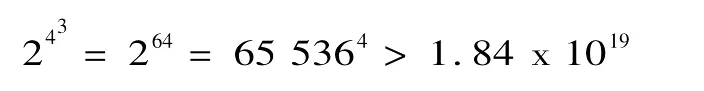
这已经是一个非常巨大的天文数字了。实际上，对于m元论域上2mn个互不相当的n元关系，人们感兴趣的只是其中很小的一部分。

三、n元关系的并、交、补

n元关系可以简称关系，当p是P的共仅属性时，就称p为P的关系。

(一)并关系

并关系就是两个集的并集所具有的关系，是原先两个集的关系的并。设关系p、q、r分别是集P、Q、R的关系，若R是P、Q的并集，则称关系r是关系p、q的并关系。

以3元集{四川，贵州，西藏}为论域，满足2元关系“…比…海拔高”的2目组集P是集{(西藏，四川)，(西藏，贵州)，(贵州，四川)};满足 2元关系“…比…海拔低”的2目组集Q是集{(四川，贵州)，(四川，西藏)，(贵州，西藏)}。集P和集Q的并集R是{(西藏，四川)，(西藏，贵州)，(贵州，四川)，(四川，贵州)，(四川，西藏)，(贵州，西藏)}，并集R中所有的2目组都满足2元关系“…与…的海拔高度不相等”。因此，2元关系“…与…的海拔高度不相等”是2元关系“…比…海拔高”和2元关系“…比…海拔低”的并关系，即r是p和q的并关系。

(二)交关系

交关系就是两个集的交集所具有的关系，是原先两个集的关系的交。设关系p、q、r分别是集P、Q、R的关系，若R是P、Q的交集，则称关系r是关系p、q的交关系。

以3元集{长江，黄河，珠江}为论域，满足2元关系“…比…长”的2目组集P是{(长江，黄河)，(长江，珠江)，(黄河，珠江)};满足2 元关系“…与…不一样长”的2目组集Q是{(长江，黄河)，(长江，珠江)，(黄河，长江)，(黄河，珠江)，(珠江，长江)，(珠江，黄河)}。集P和集Q相乘所得的交集R是{((长江，黄河)，(长江，珠江)，(黄河，珠江)}，显然，交集R仍然是集P，所以，集R满足2元关系“…比…长”。这个关系正是集P的关系“…比…长”和集Q的关系“…与…不一样长”的交关系，即r是p和q的交关系。

(三)补关系

设关系p、r分别是集P、R的关系，若R是P的补集，则称关系r是关系p的补关系。以～p表示p的补关系，～p读作“补p”。

以4 元集{1，2，3，4}为论域，满足 2 元关系“…等于…”(p)的 2 目组集P是{(1，1)，(2，2)，(3，3)，(4，4)}，论域上除此之外的其它 2 目组所组成的2 目组集R是{(1，2)，(1，3)，(1，4)，(2，1)，(2，3)，(2，4)，(3，1)，(3，2)，(3，4)，(4，1)，(4，2)，(4，3)}，这个 2 目组集R满足的关系是“…不等于…”(r)。因此，r关系“…不等于…”就是p关系“…等于…”的补关系，反之，p关系“…等于…”就是r关系“…不等于…”的补关系。

显然，论域上满足某个关系的n目组和满足它的补关系的n目组就是该论域上的全部n目组。比如，满足2元关系“…小于…”的2目组和满足它的补关系“…不小于…”(2元关系)的2目组就是该论域上的所有2目组，亦即论域上所有2目组都在满足“…小于…”关系的2目组集和满足“…不小于…”关系的2目组集的并集之中。

四、n元全关系和n元空关系

(一)n元全关系

论域U上的n目组集Un的所有n目组所满足的关系，就称为n元全关系。

以3元集{长江，黄河，珠江}为论域U，这个论域上的一个1目组集是{(长江)，(黄河)，(珠江)}，由于“…是中国的河流”为该1目组集中所有的1目组所满足，故“…是中国的河流”就是论域U上的1元全关系。而“…是中国最长的河”就不是该论域上的1元全关系，因为只有其中一个真子集所满足。论域{长江，黄河，珠江}上的一个2目组集是{(长江，长江)(长江，黄河)，(长江，珠江)，(黄河，长江)，(黄河，黄河)，(黄河，珠江)，(珠江，长江)，(珠江，黄河)，(珠江，珠江)}，由于“…和…并存”为该2目组集中所有的2目组所满足，故“…和…并存”就是论域{长江，黄河，珠江}上的2元全关系。而关系“…比…长”、“…比…短”，以及“…与…不一样长”就不是该论域上的2元全关系，因为他们都是只为其中的某些真子集所满足的关系。

对于不同的n，Un是不同的，如U0为U的0目组集，即{()}，U1为U的1目组集，U2为U的2目组集，U3为U的3目组集，……因此，对应于不同的n，n元全关系也是不同的。以“人”为论域，“…是制造和使用生产工具的动物”就是“人”这个论域上的1目组集的1元全关系;“…认识或者不认识…”就是“人”这个论域上的2目组集的2元全关系;“…的岁数介于或者不介于…的岁数和…的岁数之间”就是“人”这个论域上的3目组集的3元全关系;……

由于集P与其补集～P的并集是论域U，所以，关系p以及补关系～p的并关系就是n元全关系。以3元集{1，2，3}为论域，满足关系“…小于…”的2 目组集是{(1，2)，(1，3)，(2，3)}，满足其补关系“…不小于…”的补集～P是{(1，1)，(2，1)，(2，2)，(3，1)，(3，2)，(3，3)}，集P与其补集～P的并集R是{(1，1)，(1，2)，(1，3)(2，1)，(2，2)，(2，3)(3，1)，(3，2)，(3，3)}，它所满足的关系r是“…小于…”和“…不小于…”的并关系，即“…小于或者不小于…”，这一关系是论域{1，2，3}上的一个2元全关系，因为它为论域{1，2，3}上2目组集中的所有2目组所满足。

我们知道，0目组是空组。在任意的m元论域上只有唯一的一个0目组“()”，因此，0目组集只有唯一的一个元()，并且任何论域上的0目组集都是相同的，即{( )}，故，0目组集既是一个单独集又是一个全集，但不是一个空集而是其中有一个元即0目组()的1元集{()}。0目组所具有的共仅属性，就是0元全关系，即是为而且只为0目组具有的属性，它可以表述为“…在论域上”或者“有…存在”。比如，我们知道某种空想(相当于0目组)确实是存在的，尽管符合空想的事物并不存在，虽然没有“美人鱼”、“龙王爷”、“以太”、“燃素”之类的个体存在，但确实有“空想美人鱼”、“空想龙王爷”、“空想以太”、“空想燃素”的存在。这就是0目组满足的全关系。

(二)n元空关系

空关系就是没有个体能满足的关系，是没有n目组满足的关系。空关系可表述为“不在论域上”或者“不存在”。

空集Φ是无元之集，是任何集的子集，也是n目组集的子集，是没有n目组的n目组集，因此，任何n目组集都有一个共同的子集，即空集。由于空集一无所有，所以它只满足空关系“不在论域上”，并且，由于空集Φ是不同的Un的一个共同的子集，因此，对应于不同的n，n元空关系都是相同的，即“不在论域上”。

在集的运算中，由于某个集P与其补集～P的交集是空集，故关系p与其补关系～p的交关系就是空关系。以3元集{1，2，3}为论域，满足关系“…小于…”的 2 目组集是{(1，2)，(1，3)，(2，3)}，满足其补关系“…不小于…”的补集～P是{(1，1)，(2，1)，(2，2)，(3，1)，(3，2)，(3，3)}，集P与其补集～P的交集就是空集Φ，这一空集Φ所满足的关系就为空关系“不在论域上”。

五、2元关系

在n元关系中，2元关系是一种最普遍最常见的关系。对于2元关系本身，有一些需要引起注意和研究的关系和性质，前者如逆关系、连关系，后者如对称性、传递性、自反性。

(一)2元关系的前域、后域和域

1.2 元关系的前域

设P⊂U2，且，p为P的共仅属性，则2元关系p的前域D(p)为:由任意的x组成之集，使得对于某个y，(x，y)∈P，亦即:

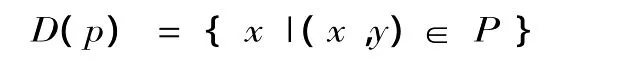
2元关系是为2目组满足的关系。在某个2目组中，位置在前的个体称为关系前项，位置在后的个体称为关系后项。2目组(穆铁柱，朱建华)满足2元关系“…比…个子高”，在这个2目组中，“穆铁柱”就是2元关系“…比…个子高”的关系前项，“朱建华”是关系后项。

2元关系的前域就是由论域中满足2元关系的2目组中的关系前项的个体为元所组成的集。以4 元集{1，2，3，4}为论域，满足 2 元关系“…大于…”的2 目组有 6 个，即(2，1)、(3，1)、(3，2)、(4，1)、(4，2)、(4，3)，其中满足 2 元关系“…大于…”的关系前项分别是2，3，4，因此，由它们所组成的集{2，3，4}就是论域{1，2，3，4}上的满足 2 元关系“…大于…”的前域D(p)。以集{上海，北京，天津，苏州}为论域，满足2元关系“…比…人口多”的2目组有6个，即(上海，北京)、(上海，天津)、(上海，苏州)、(北京，天津)、(北京，苏州)、(天津，苏州)，其中满足2元关系“…比…人口多”的关系前项分别是上海，北京，天津，因此，由它们所组成的集{上海，北京，天津}就是论域{上海，北京，天津，苏州}上的满足2元关系“…比…人口多”的前域D(p)。

2.2 元关系的后域

设P⊂U2，且p为P的共仅属性，则2元关系p的后域C(p)为:由任意的y组成之集，使得对于某个x，(x，y)∈P，亦即:

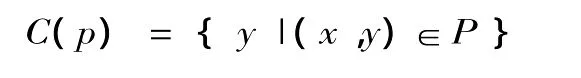
2元关系的后域就是由论域中满足2元关系的2目组中的关系后项的个体为元所组成的集。前述以4元集{1，2，3，4}为论域，满足2元关系“…大于…”的后域C(p)就是{1，2，3};以集{上海，北京，天津，苏州}为论域，满足2元关系“…比…人口多”的后域C(p)就是{北京，天津，苏州}。

3.2 元关系的域

2元关系的域F(p)就是由满足某种2元关系的个体为元组成的集。其中，满足2元关系的个体包括关系的前项的个体和后项的个体，因此，2元关系的域F(p)就是其前域和后域的并集。用符号表示为:

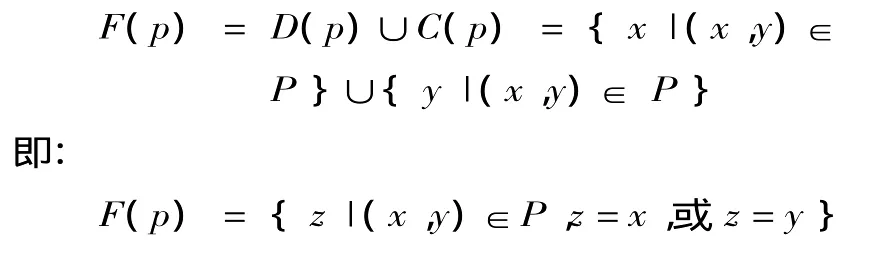
以4元集{1，2，3，4}为论域，满足 2 元关系“…大于…”的前域D(p)是{2，3，4}，后域C(p)是{1，2，3}，故，这个论域上的 2元关系的域F(p)为:

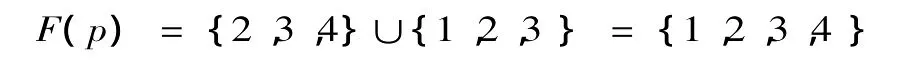
以4元集{上海，北京，天津，苏州}为论域，满足2元关系“…比…人口多”的前域D(p)是{上海，北京，天津}，后域C(p)是{北京，天津，苏州}，故，这个论域上的2元关系的域F(p)为:

F(p)={上海，北京，天津}∪{北京，天津，苏州}={上海，北京，天津，苏州}

“…是…的父亲”是以“人”为论域的2元关系，其前域是所有满足这个关系的前项的人的集合，如曹操(曹植之父)、苏洵(苏轼之父)、周树人(周海婴之父)、金正日(金正恩之父)等等，都是2元关系“…是…的父亲”的前域之元，即D(p)={x|x是有子女的男人}。而这个关系的后域是一切人，即C(p)={y|y是人}，因为任何人都有父亲。因此，这一关系的域是F(p)={x|x是有子女的男人}∪{y|y是人}={z|z是人}，即一切人。

(二)逆关系、连关系与对称性、传递性、自反性

1.逆关系与对称性

(1)2元关系的逆关系

设有两个集P、P'⊂U2，且，p、p'分别为集P、P'的共仅属性，p'为p的逆关系，当且仅当，(x，y)∈P，则(y，x)∈P'。这就是说，如果关系p的后域是另一关系p'的前域，并且关系p的前域是关系p'的后域，那么这两个关系间就具有逆关系。

以“人”为论域，关系p“…杀害…”的前域D(p)={x|x是杀害别人的人}，其后域C(p)={y|y是被杀害的人};关系p'“…被…杀害”的前域D(p')={x|x是被杀害的人}，其后域C(p')={y|y是杀害别人的人}。由于关系p的前域是关系p'的后域，并且，关系p的后域是关系p'的前域，因此，关系“…杀害…”的逆关系是“…被…杀害”，反之亦然，二者互为逆关系。

以“国家”为论域，关系“…侵略…”与“…被…侵略”互为逆关系。以“自然数”为论域，关系“…大于…”与“…小于…”互为逆关系。

(2)2元关系的对称性

若关系p的逆关系也是关系p，即，如果(x，y)∈P则(y，x)∈P，那么称关系p具有对称性。关系p具有对称性是2元关系中关系p与其逆关系正好相同时的特殊情况。

以“国家”为论域，关系“…与…相邻”的逆关系仍然是“…与…相邻”，因此称关系“…与…相邻”是具有对称性的2元关系。即，若x与y相邻，则必有y与x也相邻。

以“人”为论域，关系“…和…是同学”的逆关系仍然是“…和…是同学”，因此称关系“…和…是同学”是具有对称性的2元关系。即，若x与y是同学，则必有y与x也是同学。

2.连关系与传递性

(1)2元关系的连关系

设有3 个集P、Q、R⊂U2，且，p、q、r分别为P、Q、R的共仅属性，r是p、q的连关系，当且仅当，(x，y)∈P，且(y，z)∈Q，则(x，z)∈R。这就是说，对于任意的两个关系p、q，当p的后项就是q的前项时，就必然存在连关系r，r以p的前项为其前项，以q的后项为其后项。

以“人”为论域，关系“…是…的哥哥”为关系p，以“…是…的父亲”为关系q，当p的后项与q的前项完全相同时，关系p与关系q就有连关系r，r就是“…是…的伯父”。亦即，若x是y的哥哥，并且y是z的父亲，则x一定是z的伯父。论域为“人”，关系p为“…是…的邻居”，关系q为“…是…的同学”，当p的后项与q的前项完全相同时，关系p与关系q就有连关系r，r就是“…是…同学的邻居”。亦即，若x是y的邻居，并且y是z的同学，则x一定是z的同学的邻居。

对于任意两个2元关系，只要当关系p的后项与q的前项完全相同时，那么关系p的前项与关系q的后项就必定满足一种关系，这种关系就是关系p与关系q的连关系r，尽管这种关系有时不容易用一个短语说清楚，但它一定是存在的。

(2)2元关系的传递性

若p是p、p的连关系，即，如果(x，y)∈P且(y，z)∈P则(x，z)∈P，那么就称p具有传递性。具有传递性的2元关系是与连关系有关的p、q、r均为p时的特殊情况。

以“自然数”为论域，“…大于…”为关系p1，显然，关系p1与关系p1的连关系仍然是p1。因此，称“…大于…”是具有传递性的2元关系:若x＞y，且y＞z，则x＞z。

以“人”为论域，“…是…的哥哥”为关系p2，显然，关系p2与关系p2的连关系仍然是p2。因此，关系“…是…的哥哥”具有传递性:若x是y的哥哥，且y是z的哥哥，则x一定是z的哥哥。

3.2 元关系的自反性

设集P⊂U2，p为P的共仅属性，若对于任意的x，必有(x，x)∈P，则称关系p具有自反性。

以某集的“n元子集之集”为论域，关系“…包含…”就具有自反性，即，任一集x包含x自身。以“人”为论域，关系“…认识…”具有自反性。张三自己认识自己，王五自己认识自己。以“自然数”为论域，关系“…等于…”具有自反性;以“几何图形”为论域，关系“…相似于…”也具有自反性。

一个关系具有自反性，是指任一个体与其自身必定满足该关系。因此，在一个2元关系中，只要同一个体必定在其前域和后域中同时出现，则这一2元关系一定具有自反性。

六、对传统形式逻辑和数理逻辑的相关讨论

(一)对传统形式逻辑的讨论

通常，习惯于把1(n=1)元关系称为“性质”，2元或2元以上的多(n＞1)元关系才称为“关系”。其实，性质和关系只不过是同一事物的两个不同的侧面:“关系”是多(n＞1)目组的性质，也是一种性质;而“性质”则是1(n=1)目组的关系(即1元关系)，也是一种关系。迄今，流行的传统形式逻辑读本给概念内涵下的定义是:“概念的内涵就是指反映在概念中的对象的本质属性。”［1］有些书不叫“本质属性”，而叫“特有属性”，有些书则叫“固有属性”。无论流行的传统形式逻辑读本用什么属性定义概念的内涵，传统形式逻辑所研究的“概念的内涵”就是相当于我们这里讲的1元关系p。流行的传统形式逻辑读本给概念外延下的定义是:“概念的外延，就是指具有概念所反映的本质属性的对象。”［2］显然，传统形式逻辑研究的“概念的外延”就相当于我们这里讲的与1元关系p相对应的U1的确定的子集P。关于作为传统形式逻辑研究的命题系列的出发点的性质命题(或称直言命题、简单命题)，流行的传统形式逻辑读本的定义是:“性质命题，就是断定思维对象性质的简单命题。”［3］传统形式逻辑研究的性质命题就是基于1元关系命题的复合命题，譬如，为传统形式逻辑所研究的全称肯定命题“所有在座的都是中国人”(其符号表达式为:所有S都是P)，实际就是当代形式逻辑所研究的外延合取命题:“在座的第一个人是中国人，并且，在座的第二个人是中国人，并且，…，并且，在座的第i个人是中国人，并且，…，并且，在座的最后一个人是中国人”(当代形式逻辑的符号表达式为:p(e1)∧p(e2)∧…∧p(ei)∧…∧p(em)。这是m个传统形式逻辑所研究的单称命题(性质命题的一种)构成的合取命题)。又如，为传统形式逻辑研究的特称肯定命题“有些在座的是中国人”(其符号表达式为:有些S是P)，实际就是当代形式逻辑所研究的外延析取命题:“在座的第一个人是中国人，或者，在座的第二个人是中国人，或者，…，或者，在座的第i个人是中国人，或者，…，或者，在座的最后一个人是中国人”(当代形式逻辑的符号表达式为:p(e1)∨p(e2)∨…∨p(ei)∨…∨p(em)。这是m个传统形式逻辑所研究的单称命题构成的析取命题)。传统形式逻辑从诞生之日起，从来就不研究多元关系概念。虽然在一些后来出版的传统形式逻辑读本中增添了关于关系命题的内容，可是，仍然不研究多元关系和真正的普遍有效的关系推理，譬如，流行的传统形式逻辑读本介绍的对称性关系推理是:

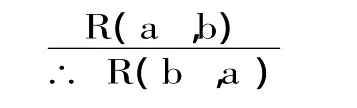
或者表达为:

反对称性关系推理是:

或者表达为:

专业人士一眼就能看出，上述2式不是有效式，故而，不是推理式。

传统形式逻辑读本新增的关系命题，前无渊源后无归宿。因此，尽管从主导思想上说，传统形式逻辑是真正的名副其实的逻辑科学，其研究成果是久盛不衰的，然而从研究范围来看至少是“挂1漏n－1”的，即研究1元关系而漏掉(n－1)种关系，因此，传统形式逻辑至多只能算n分之一的逻辑。

(二)对数理逻辑的讨论

以研究内涵为主同时也研究外延的当代形式逻辑与只研究外延的数理逻辑不同。n元关系指的不是Un的一个子集P，而是它的共仅属性p。对应于Un的同一个子集P，客观世界有k个尽管互相对当然而却依旧两两不同的n元关系p1、p2、…、pi、…、pk。纯外延的数理逻辑(其实并非逻辑，而是被称为“逻辑”的离散数学)却不从内涵的角度来区分这k个互不相同的n元关系，从量上说至少是“挂1漏k－1”的，即只从外延的角度研究一种关系而漏掉(k－1)种关系，数理逻辑顶多只能算k分之1的逻辑。也正是由于它不从内涵的角度研究k个互不相同的n元关系，因此，我们称其为“纯外延的”数理逻辑［4－6］。

注:本文作者通讯地址为贵阳市花溪区贵州大学(北区)，欢迎广大读者来函交流。

［1］李小克.普通逻辑学教程［M］.北京:首都经济贸易大学出版社，2002:13.

［2］李廉.普通逻辑基础［M］.南京:南京大学出版社，1985:44.

［3］楚明锟.逻辑学:正确思维与言语交际的基本工具［M］.开封:河南大学出版社，2000:61.

［4］龚启荣.客观世界的集——兼对悖论之王“罗素悖论”的剖析［J］.重庆理工大学学报:社会科学，2011(9).

［5］龚启荣.当代形式逻辑及其在人工智能中的应用理论研究［M］.北京:电子工业出版社，2011.

［6］龚启荣.逻辑斯谛——又称“数理逻辑”的二值数学［M］.贵阳:贵州教育出版社，1998.

N-ary Relations of Objective World——Also a Discussion on Traditional Formal Logic and Mathematical Logic Being at Most 1/x of Logic

GONG Qi-rong
(Guizhou University，Guiyang 550025，China)

The prospect of the study onn-ary relations of objective world by contemporary formal logic is incomparable that traditional formal logic and mathematical logic can do.To view the dominant ideas，traditional formal logic is a veritable science of logic，which just studies on 1-ary relations，but not on multivariate relations and generally effective relation inference.Therefore，traditional formal logic is at most onen-th of logic.From connotation angle，mathematical logic doesn’t distinguish the equivalent but differentk n-ary relations of denotation，though 1-ary or multivariate relations is one of the study objects of mathematical logic.It is at least having 1 but losingk-1，that’s to say，mathematical logic just studies one relationship from denotation angle but losesk-1 relationship.Therefore，mathematical logic of pure denotation is at most onek-th logic.Contemporary formal logic begins to study withn-item andn-item set of universe of discourse，i.e.it does thorough study，including every field of science of logic，on all the relations among n individuals(n≥1)by confirming the different sequences of individuals in universe of discourse.

contemporary formal logic;traditional formal logic;mathematical logic;n-item;n-item set;n-ary relation

B81

A

1674－8425(2012)04－0016－09

2012－01－11

教育部人文社会科学研究项目“当代形式逻辑及其在人工智能中的应用理论研究”(07JA720006)成果。

龚启荣(1942—)，男，江西景德镇人，教授，研究方向:逻辑学、离散数学、人工智能学。

(责任编辑 魏艳君)