改进的Zernike 矩工业CT 图像边缘检测

陶 李，王 珏 ，邹永宁，伍立芬，王慧倩

(重庆大学 自动化学院 光电技术及系统教育部重点实验室ICT 研究中心，重庆400044)

1 引 言

近年来，随着工业CT 技术的迅速发展，工业CT 系统已不仅用于对物体的无损探伤和对物体内部结构的定性分析和质量评价，还广泛应用于物体内部结构尺寸和材料密度的定量测量，因此提高测量精度和测量速度以及自动化程度已成为工业CT 领域当前研究的重点之一。通过工业CT图像测量物体的几何尺寸主要包括: 点与点之间的距离、目标面积、表面积和体积等。

通过工业CT 图像实现对被测物体几何尺寸实时精确的测量，首先要提高工业CT 图像的边缘定位精度和速度，这直接影响后续测量结果的精度和速度。提高图像测量精度和速度主要通过:(1) 提高工业CT 系统的硬件性能，如提高扫描系统速度和探测系统精度等; ( 2) 利用软件方法，如提高图像边缘定位算法的精度和速度等。前者设备成本高、周期长而且在精度和速度的提高上受限; 后者设备成本低、速度快、易于更新。如果能够将CT 图像边缘定位在亚像素级别，则可直接提高测量系统精度。

亚像素边缘定位算法具有边缘定位精度高等优点，常用于亚像素边缘检测当中，方法主要包括: 基于一阶微分期望值、小波变换［2］、空间矩［3］、插值、拟合［4］等，其中，Haralick［5］等人提出的基于Facet 模型的亚像素级边缘检测算法，通过3 次多项式拟合Facet 模型，再根据方向导数信息求得二阶导数过零点，最终确定亚像素边缘位置。该方法稳定可靠，能定位图像微小细节，从而提高检测精度，但是因为运算量巨大而耗时［6］，不能同时满足精度和速度的要求［7］。利用基于Zernike 正交复数矩［8］的亚像素边缘检测算法在单位圆内具有正交性，可减少亚像素边缘检测所需要的模板数目、降低函数的阶数、增强抗干扰能力，从而提高边缘定位精度［9］，但是运算耗时不能满足实时在线测量要求。因此，为了提高工业CT 图像边缘检测算法的精度和速度，本文研究了改进的Zernike 矩边缘检测算法，该方法不仅能够高精度定位工业CT 图像边缘，而且能够大幅度提高定位速度。通过高精度定位图像的亚像素边缘，保证了后续图像测量的精度;在保证精度的前提下，算法大幅减少运算时间，提高检测速度，实现了实时在线工业CT 图像的高精度测量。

2 Zernike 矩边缘检测原理

2．1 Zernike 矩原理

根据复数域Zernike 多项式的定义，可得到具有正交、旋转不变特性的Zernike 矩。Zernike 的n阶多项式定义为［10］:

式中:n≥0，且n- |m|为偶数，实值多项式Rnm由下式给出:

Zernike 多项式在单位圆x2+y2=1 内是正交的，即:

当且仅当n=p，m=q，公式( 3) 成立。其中* 表示复共轭。

一幅连续图像f(x，y) 的n阶m次Zernike 矩定义为:

式中:Vmn( ρ，θ) =Rmn( ρ) eimθ为积分核函数，* 为复共轭，ρ 为圆点到点(x，y) 的矢量长度，θ 角为矢量长度ρ 与x轴之间逆时针方向的夹角。Rmn( ρ) 是径向多项式，定义为:

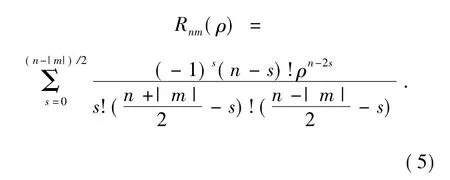
对离散的数字图像而言，其表示形式为:

Zernike 矩的最重要性质是旋转不变性［10］，一幅图像旋转θ 角度后，A'mn=Amne-imθ，即图像旋转前后的Zernike 矩只改变相位角，而幅度保持不变。

2．2 Zernike 矩边缘检测算法

Ghosal［11］等人提出基于Zernike 矩的边缘检测算法，其基本原理是通过建立Zernike 矩与图像边缘检测理想模型的4 个边缘参数的关系，分别求解矩而得到图像模型4 个边缘参数，在将参数与预设的阈值进行比较判定为边缘点之后，通过计算来精确定位图像边缘位置。利用Zernike 矩的旋转不变性旋转图像后，可以容易地计算出4 个参数，进而实现对边缘的精确定位。Zernike 矩是积分型算子，对噪声不敏感，抗噪能力较强。

二维平面亚像素边缘检测理想边缘模型如图1所示。理想的采样区域为单位圆，直线L被单位圆包含的部分代表理想边缘，圆内L两侧的灰度值分别为H和H+k，k为两侧的灰度差，l表示原点到边缘的理论距离值，θ 表示线段l与x轴之间的夹角。

图1 二维平面亚像素边缘检测理想模型Fig.1 Ideal model of two-dimensional sub-pixel edge detection

若把图像边缘顺时针旋转θ 角，线段l将与x轴平行，则:

式中，f'(x，y) 是图像经过顺时针旋转后的得到的边缘函数。利用Zernike 矩进行边缘定位时，需要用到3 个不同阶次的Zernike 矩，分别是A00，A11，A20。这些不同阶次的Zernike 矩相对应的积分核函数分别为:V00=1，V11=x+iy，V20=2x2+2y2-1。

旋转后图像的Zernike 矩与原图像的Zernike矩之间的关系为:

由于式(7) 是A＇11的虚部，因此有:

式中Re［A11］，Im［A11］分别为A11的实部和虚部。因此可以求出θ 角，即:

式中，(xs，ys) 是边缘的亚像素坐标。

综上所述，利用3 个Zernike 矩A00，A11，A20可以求解理想边缘模型的4 个参数θ，l，k，h，并可以根据4 个参数计算出边缘点的亚像素坐标。

2.2.1 Zernike 矩算子的7 ×7 模板

采用Zernike 矩算子进行图像边缘检测，需要对每个边缘点计算得到4 个参数，用来判断该像素点是否为边缘点。计算不同阶次的Zernike 矩模板是对图像进行亚像素边缘检测的前提条件。原Ghosal 算法仅仅推导了Zernike 矩的5 ×5 模板中A00，A10，A20的系数，在Ghosal 等人的5 ×5 模板基础上，高世一等人计算了Zernike 矩的7 ×7 模板系数［13］，这是因为实际CT 图像边缘不是理想阶跃边缘，边缘存在灰度过渡，而采用7 ×7 模板能够细化边缘，从而更好地抑制CT 系统带来的噪声。

2.2.2 消除模板效应

仔细分析Ghosal 算法能够发现，Ghosal的Zernike矩亚像素定位精度虽然较高，却忽略了模板效应导致的边缘坐标系数计算不精确问题。模板效应是指Zernike 矩算子根据实际需求要选择不同大小的模板，而使边缘坐标计算产生偏差［14］。假设所选的模板大小为N×N，由于边缘点坐标公式的推导和计算都在单位圆内进行，而在实际边缘检测过程中，模板是从左到右、从上到下移动着和图像进行卷积计算，这时模板每次移动覆盖了被检图像上N2个像素点，单位圆的半径则变为N/2，因此需要把计算出来的到边缘的垂直距离l放大为Nl/2，相应的式(12) 变换为:

3 算法改进

由于Zernike 矩边缘算法需要将图像和模板进行卷积计算，运算量随着图像的大小而增大。虽然它检测精度高，但算法的运行时间较慢，不能满足对工业CT 图像边缘实时在线检测的要求，因此，本文提出了综合Sobel 的改进Zernike 矩工业CT 图像边缘检测算法。主要流程如图2 所示。

3．1 Sobel 算子边缘定位

首先利用Sobel 算子粗定位整个CT 图像可能的边缘点;

图2 算法流程图Fig.2 Algorithm flowchart

Sobel 边缘检测的主要目的是找出全部边缘可能存在的位置，在Sobel 算子粗定位之前，需要对CT 图像进行预处理，用来减少粗检时产生多余的伪边缘。

利用Sobel 边缘算子检测图像边缘的步骤如下:

(1) 对CT 图像上灰度值为f(x，y) 的点(x，y)在x，y方向上分别计算灰度值的偏导数f'x与f'y，公式如下:

式中:f'x(x，y) ，f'y(x，y) 分别表示x，y方向的一阶微分，G［f(x，y) ］为梯度。

(3) 设阈值为t，当G［f(x，y) ］＞t时，即可判定该点即为图像可能的边缘点。然后将这些可能的边缘点保存在数组中。

3．2 Zernike 矩边缘精确定位

在对整个图像使用Sobel 算子进行粗检后，利用Zernike 矩算子对保存在数组中可能的边缘点图像重新精确定位图像边缘，步骤如下:

(1) 将像素点和计算的7 ×7 模板进行卷积;

(2) 计算每一个像素点的边缘角度θ，k，l;

(3) 如果像素点的参数满足判定条件k≥kt且l≤lt;则利用式(13) 计算亚像素边缘坐标。

3.3 边缘点判据

从3.2 步骤(3) 可以看出，在Zernike 矩算子中利用式(9) 和式(11) 求出4 个参数之后，需要对参数判断是否满足k≥kt且l≤lt，其中kt和lt分别是阶跃强度阈值和圆心到边缘的距离阈值，只有当上面的条件成立时，才能将像素点判定为边缘点并进行计算。通过分析可知，若强度阈值太小，则产生的伪边缘较多，强度阈值太大虽然能抑制伪边缘，但是会丢失部分真实边缘，效果也不理想。由式(11) 可知，k是关于A＇11和l的函数，因此可以得到k的关系式:

而其中:

令A'11=amp，则k=1．5(1 -l2)-3/2amp=λ·amp

式中，λ =1．5( 1 -l2)-3/2，当l取值较小时，则有:

为了细化边缘图像，通常取l为＜0.3 的正数，l与λ 的关系见表1。因此，使用amp代替k没有损失图像边缘检测精度，其主要目的是减少算法的运算量。

表1 l 与λ 之间的关系Tab．1 Relationship between l and λ

4 试验与结果分析

4.1 改进算法的边缘检测精度

利用Matlab2008Ra 工具验证加速算法不损失图像边缘定位精度。实验所用的为一幅800 pixel×800 pixel 工业CT 图像［16］，如图3 所示。

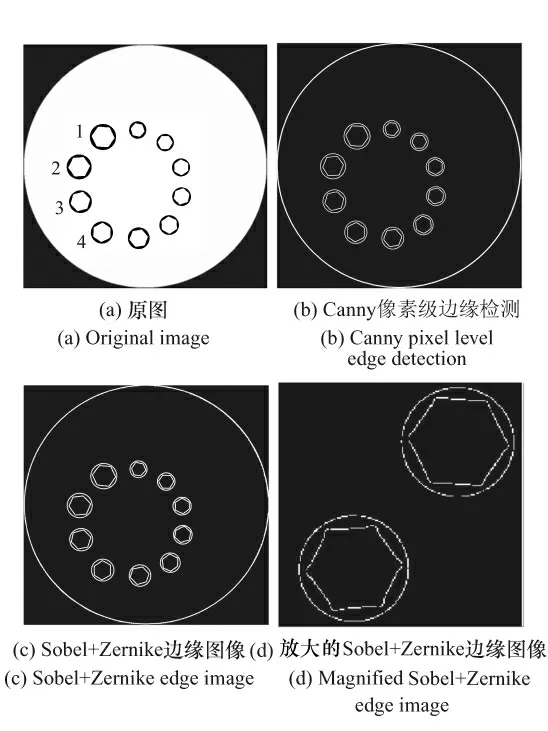
图3 工业CT 图像边缘检测结果比较Fig.3 Comparison of industrial CT image edge detection results

从图3( b) 可以看出，Canny 边缘算子检测出的边缘图像为像素级，经过非极大值抑制后的图像边缘为单像素，但是精度达不到亚像素级别，满足不了测量需求; 图3( c) 利用改进的Zernike 矩检测出亚像素边缘，但将亚像素边缘图像局部放大后( 见图3( d) ) ，由于边缘坐标为浮点数，可能会有小的断裂［17］。

通过对边缘图像进行边缘跟踪连接［18］，能够计算出圆半径参数。表2、表3 列出了图4 中圆半径参数测量结果以及测量值与真实值的绝对误差和相对误差。

图4 运算速度检测图像Fig.4 Images of processing speed detection

表2 Sobel+Zernike 矩工业CT 图像中圆半径参数的测量Tab．2 Circle radius parameter measurement of Sobel+Zernike moment industrial CT images

表3 Zernike 矩工业CT 图像中圆半径参数测量Tab．3 Circle radius parameter measurement of Zernike moment industrial CT images

由表2、表3 可以看出，测量值较真实值偏大，使用Zernike 矩的半径测量值绝对误差＜0.24 pixel，相对误差＜0.64%; 使用改进的Zernike 矩半径测量值绝对误差＜0.24，相对误差＜0.55%;可以看出改进的Zernike 矩算法在测量精度上和原Zernike 矩算法一致，没有降低精度。

4.2 改进算法的运算速度

为了验证加速算法的有效性，对加速算法的运算时间进行了测量。运行环境为个人计算机( 配 置CPU 为DualCore AMD Athlon II X 2 2 5 0 3GHz，内存为2G) 和Matlab2008。仿真了4 个图像中不同的边缘点数量，在不同图像尺寸( 256 pixel×256 pixel、512 pixel × 512 pixel、1 024 pixel×1 024 pixel、2 048 pixel×2 048 pixel)中测量了运算时间，分析了边缘点数量对算法运算速度的影响。

从表4 中可以得出，Zernike 矩算子的边缘检测时间随着图像尺寸大小而剧增，改进的Zernike 矩算子能够大幅度减少运算时间。

表4 Sobel、zernike 矩和改进的Zernike 矩运算时间Tab．4 Computation time of Sobel，Zernike moments and improved Zernike moments (s)

图5 图像尺寸、边缘数量与加速比Fig.5 Image size，edge quantity and acceleration ratio

由图5 可以看出，图像尺寸越大，改进算法的加速比越大;图像边缘点数量多，加速比越小;边缘点数量越少，改进算法的加速比越大，加速效果也会越明显。在实际CT 图像中，边缘数量比例小于5%，因此改进算法可提高实际CT 图像的边缘检测速度。

改进的Zernike 矩算子运算时间较Zernike 矩算子快的主要原因在于该算子先利用快速的Sobel算子对整个图像进行了粗检测，缩小Zernike矩算子检测范围，再利用7 ×7 大模板的Zernike矩算子精确定位边缘。

综上所述，图像中边缘点个数决定了整个算法的运算时间。在一幅图像中当边缘点比例为n≈87%时，两个算子的运行时间才相等。然而在任何情况下边缘点比例n≤50%。考虑到Soble算子粗检出可能的边缘点会多于实际边缘点数量，如果Sobel 算子粗检出的可能边缘点数量为真实边缘点数量的2 倍，则n≈48%。在实际工业CT 图像边缘检测中，由于存在噪声和灰度过渡，Sobel 算子会粗检出比真实边缘多的边缘点，验证了改进后的Zernike 矩算法能够大幅提高运算速度。

5 结 论

研究了一种改进的Zernike 矩的工业CT 亚像素边缘检测算法，并进行了工业CT 图像实验。实验结果表明，该方法的边缘定位精度无损失，运算速度快。运用该算法能够精确定位工业CT 图像边缘亚像素位置，在定位精度上和Zernike 矩保持一致，半径测量值绝对误差＜0.1 mm，相对误差＜0.5%;在速度上比单独使用Zernike 矩算子快，在实际CT 图像中，检测速度提高了70%。因此该算法适用于对检测精度和实时在线性要求较高的工业CT 图像测量。

［1］ 庄天戈.CT 原理与算法［M］.上海:上海交通大学出版社，1992.ZHUANG T G.CT Theory and Arithmetic［M］. Shanghai:Shanghai Jiaotong University Press，1992.( in Chinese)

［2］ 林晓梅，李琳娜，牛刚，等.基于小波边缘检测的图像去噪方法［J］.光学 精密工程，2004，12(1) :88-93.LIN X M，LI L N，NIU G，et al.. Image de-noising based on wavelet edge detection［J］.Opt． Precision Eng，2004，12(1) :88-93.( in Chinese)

［3］ 郭玉波，姚郁，遆晓光.基于空间矩的圆标记中心亚像素定位算法［J］.吉林大学学报，2009，39(1) :160-163.GUO Y B，YAO Y，DI X G. Subpixel location algorithm for circle target center based on spatial moment［J］.J． Jilin University( Engineering and Technology Edition) ，2009，39(1) :160-163.( in Chinese)

［4］ 尚雅层，陈静，田军委.高斯拟合亚像素边缘检测算法［J］.计算机应用，2011，31(1) :179-181.SHANG Y C，CHEN J，TIAN J W. Sub-pixel edge detection algorithm based on Gauss fitting［J］.J． Computer Appl.，2011，31(1) :179-181.( in Chinese)

［5］ HARALICKR M. Digital step edges from zerocrossing of second directional derivatives［J］.IEEE T． Pattern Anal．，1984，6(1) :58-68.

［6］ HU Z F，DANG H SH，LI X R. A novel fast subpixel edge location method based on sobel-OFMM［C］//Proc. of the IEEE International Conference on Automation and Logistics，Sept 1-3，2008，Qingdao，China，2008

［7］ 王云慧，马军山，孙军.基于边缘检测的七阶矩方法［J］.计算机应用，2010，30( S1) :159-161.WANG Y H，MA J SH，SUN J. Seven-order moments based on edge detection［J］.J． Computer Appl．，2010，30( S1) :159-161.( in Chinese)

［8］ 魏本征，赵志敏，华晋.基于改进形态学梯度和Zernike 矩的亚像素边缘检测方法［J］.仪器仪表学报，2010，31(4) :838-844.WEI B ZH，ZHAO ZH M，HUA J. Sub-pixel edge detection method based on improved morphological gradient and Zernike moment［J］.Chinese J． Sci． Instrument，2010，31(4) :838-844.( in Chinese)

［9］ XIANG L M，WAN T，HE C ZH. A stable least squares ellipses fitting algorithm based on Zernike moments［J］.Advanced Mater． Res．，2011，142:199-203.

［10］ GHOSAL S，MEHROTRA R. Orthogonal moment operators for subpixel edge detection［J］.Pattern Recognition，1993，26(2) :295-306.

［11］ Al-RAWI M. Fast Zernike moments［J］.Real-Time Image Proc．，2008，3(1-2) :89-96.

［12］ LIANG B，DONG M L，WANG J，et al. Sub-pixel location of center of target based on Zernike moment［J］.SPIE，2010，7544:75443A.

［13］ 高世一，赵明扬，张雷，等.基于Zernike 正交矩的图像亚像素边缘检测算法改进［J］. 自动化学报，2008，34( 9) :1163-1168.GAO SH Y，ZHAO M Y，ZHANG L，et al.. Improved algorithm about subpixel edge detection of image based on Zernike orthogonal moments［J］.Acta Automatica Sinica，2008，34(9) :1163-1168.( in Chinese)

［14］ FANG Y H，XIAO H M，WANG B L. A sub-pixel feature extraction method for CT image based on Zernike moments［C］//2nd IEEE International Conference on Advanced Computer Control( ICACC 2010) ，Mar 27-29，2010，Shenyang，China，2010:539-542.

［15］ 曲迎东，李荣德，白彦华，等.高速的9 ×9 尺寸模板Zernike 矩边缘算子［J］.光电子·激光，2010，21( 11) :1683-1687.QU Y D，LI R D，BAI Y H，et al.. A high-speed Zernike moments edge operator based on 9 ×9 masks［J］.J．Optoelectronics·Laser，2010，21(11) :1683-1687.( in Chinese)

［16］ 曲迎东，崔成松，陈善本，等.Soble-Zernike 矩亚像素边缘算子的影响因素分析［J］.光电工程，2005，32(7) :71-73.QU Y D，CUI CH S，CHEN SH B，et al.. Analysis of the influencing factors on subpixel Sobel-Zernike moments edge operator［J］.Opto-electronic Eng.，2005，32(7) :71-73.( in Chinese)

［17］ 刘丰林，乔桂锋，邹斌.工业CT 图像圆精确测量［J］.光学 精密工程，2009，11(17) :2842-2848.LIU F L，QIAO G F，ZOU B. Precise measurement of circles in industrial computed tomographic images［J］.Opt． Precision Eng.，2009，11(17) :2842-2848.( in Chinese)

［18］ 向才兵，曾理.综合CV 和Facet 模型的裂纹边缘检测［J］.计算机工程与应用，2011，47(2) :153-155.XIANG C B，ZENG L. Crack edge detection using comprehensive CV and facet model［J］.Computer Eng． Appl.，2011，47(2) :153-155.( in Chinese)

［19］ 马睿，曾理，卢艳平.工业CT 图像的亚像素级面积测量［J］.计算机工程与应用，2009，45(15) :233-236.MA R，ZENG L，LU Y P. Sub-pixel area measurement method of ICT image［J］.Computer Eng． Appl.，2009，45(15) :233-236.( in Chinese)

［20］ AGNIESZKA L. Multiscale moments-based edge detection［C］//Eurocon 2009. IEEE，May 18-23，2009，St.-petersburg，USA，2009:1414-1419.

［21］ 陈娟，陈乾辉，师路欢，等.图像跟踪中的边缘检测技术［J］.中国光学与应用光学，2009，2(1) :46-52.CHEN J，CHEN Q H，SHI L H，et al.. Edge detection technology in imaging tracking［J］.Chinese J． Optics and Appl．Optics，2009，2(1) :46-52.( in Chinese)

［22］ 袁理，叶露，贾建禄.基于Hough 变换的椭圆检测算法［J］.中国光学与应用光学，2010，3(4) :379-384.YUAN L，YE L，JIA J L. Ellipse detection algorithm based on Hough transforms［J］.Chinese J． Opt． and Appl． Optics，2010，3(4) :379-384.( in Chinese)