修改的BWRS状态方程
2012-10-29苑伟民
苑伟民
(中国石化天然气分公司广西液化天然气工程项目部,广西北海 536000)
0 引言
在天然气工程中,在进行输气管道水力热力计算时需要计算天然气的热物性参数,如密度、压缩因子、焓、熵、定压热容、热容比、焦耳—汤姆逊系数等,这就需要用到状态方程,并且随着管道仿真技术的发展,对于模型精度的要求也越来越高。准确计算流体的属性和建立准确的热力学模型需要准确的状态方程[1]。
由于BWRS状态方程可用于气体和液体计算,其方程系数可由公式算得,并且有适用于很多烃类的混合规则;因此,在高密度或者含有凝液的管道仿真中BWRS是使用最广的状态方程[2]。但是,Staring给出了18种常见组分间的二元交互作用系数Kij数据,对于天然气多样化的组分还是显得有些少,有必要增添常用组分及其二元交互作用系数。其次,BWRS方程中所采用的密度单位为kmol/m3[3-8],而在国际单位制中[9],密度的单位采用kg/m3;同时在天然气稳态模拟及其他工艺计算中,需要用到BWRS方程的偏微分项,其单位制同样需要转换,如果直接修改方程系数,使其各个参数都统一为国际单位制,这样用BWRS方程来求解其他参数时就会很方便。如何对其中各参数的单位进行统一,文献 [3-8]都没有给予说明,并且这些文献中同一物性参数存在多种单位制,没有统一的单位制[10]。再次,由于BWRS状态方程是关于密度的隐式方程,如何精确并且快捷地求解该超越方程也是值得关注的。
为此,给出了改写的BWRS状态方程——MBWRS状态方程。
1 Benedict-Webb-Rubin-Starling (BWRS) 状态方程
BWRS方程是通过修正BWR方程而得到的,它保留了BWR方程中与密度关联的系数项,改变了与温度关联的系数项。BWRS方程包含了计算轻烃组分的系数,决定烃类混合物气体系数的混合规则,因此可以用于热力学性质计算和气液平衡计算。
BWRS状态方程是一个多参数状态方程,其基本形式[3-8]为:

式中p——系统压力/kPa;
ρ——气相或液相的密度/(kmol/m3);
R——通用气体常数,8.314 3 kJ/(kmol·K);
T——系统温度/K。
方程中的 11 个参数 A0,B0, C0, D0, E0,a,b,c,d,α,γ必须通过大量的实验得到。
2 改写的BWRS状态方程 (MBWRS状态方程)
2.1 因次和谐
在工程中许多实际问题目前尚不能用数学分析求解。有时虽然导出偏微分方程,但它是非线性的,亦常难于得到精确解。这就不得不借助于实验,此即经验公式的来源。经验公式能近似地在一定范围内符合实际情况;经验公式的导出又和涉及某一物理现象的各种参数及其合理排列有关。借助于因次分析,把控制物理现象的参数化为无因次群,这为实验数据处理提供极大方便。
对于一个物理现象所包含的各物理量间的函数关系,如果选用一定的单位制,则其关系的函数式就确定了。若改变单位制则函数关系可能受影响,要保持函数关系不变,就必须具有特殊函数关系的结构形式。有物理意义的代数表达式或完整的物理方程是因次和谐的,或称齐次的。一个方程如果因次上齐次,则方程的表达式不随基本单位的改变而改变[11]。
下面给出将BWRS状态方程改写为无因次方程的转化公式。
2.2 BWRS方程的改写
将BWRS方程各参数改写为如表1所示的形式:

表1 BWRS方程中各参数的改写
11个参数的关联式仍保持不变,混合规则亦保持不变。于是BWRS方程转化为:

式中p——系统压力,其因次为ML-1T-2;
T——系统温度,其因次为Θ;
ρ——气相的密度,其因次为ML-3;
R′——气体常数,其因次为L2T-2Θ-1;
W——平均分子量。
上述因次的物理意义如下:长度的因次为L,质量的因次为M,时间的因次为T,温度的因次为Θ[11-12]。通过上述处理发现,方程中11个参数的量纲并未转换为1,但是,可以发现,上述公式中的参数已经不受单位制限制,由π定理可知,此时该函数关系为无因次的函数关系。
将方程 (2)中的参数改写如下,其意义仍为修改过的BWRS方程:
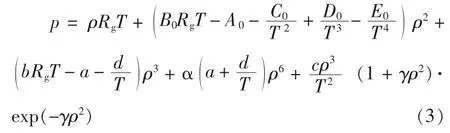
式中Rg——气体常数,其因次为L2T-2Θ-1。
2.3 二元交互作用系数的改进
Staring给出了18种常见组分间的Kij数据,但是对于天然气多样化的组分还是显得有些少,在参考商业软件的基础上,增添了一些常见组分,包括了在内的25个组分,见表2,为准确地求得天然气的物性参数提供了有力的保障。
3 方程的求解
Starling提供了纯物质的临界性质和普适化系数。一旦知道了对于流体所附加的系数值 (临界参数、分子量等),所有的状态参数都可以用己知的状态来计算。但是,很多流体模型通过流动方程计算压力和温度,用状态方程求解密度或者压缩因子[2]。由于BWRS方程中关于密度的关系式是隐式的,需要通过迭代方法来计算,使得大型管网中的密度或者压缩因子计算需要消耗大量的时间[13],用弦截法求解简单、快捷、精确。
3.1 密度的求解
将已知压力p、温度T代入式 (3)进行计算,求得气体密度ρ。为方便求解,将式 (3)改写为如下形式,并用弦截法求解[14]。

弦截法迭代公式为:
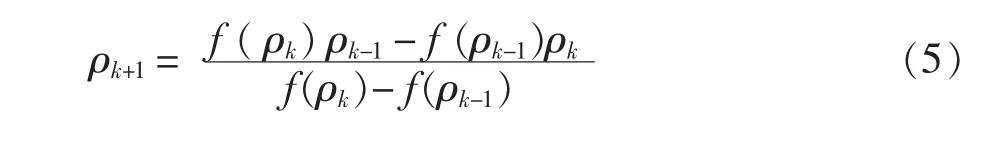
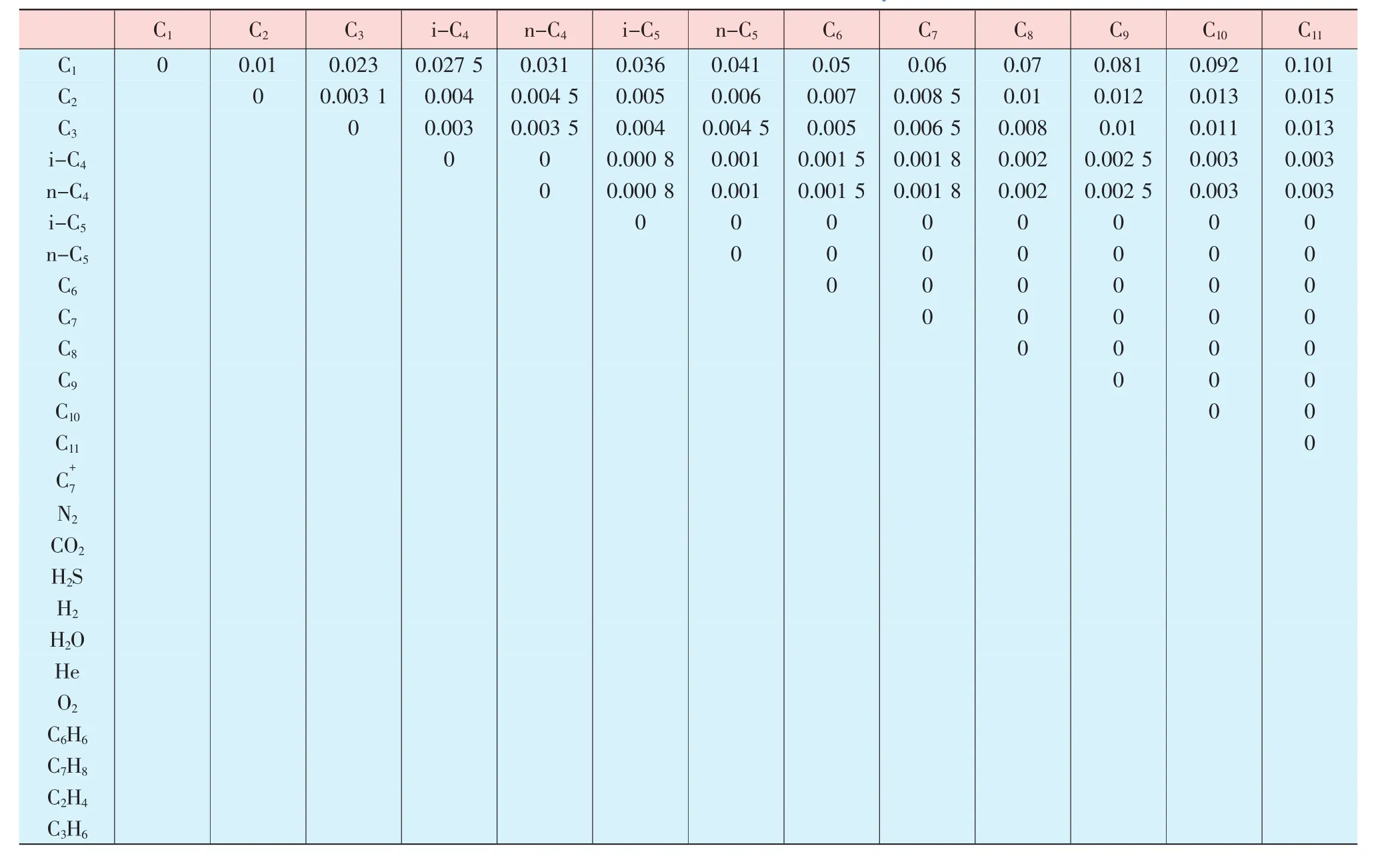
表2 BWRS修改模型中的二元交互作用系数Kij(待续)
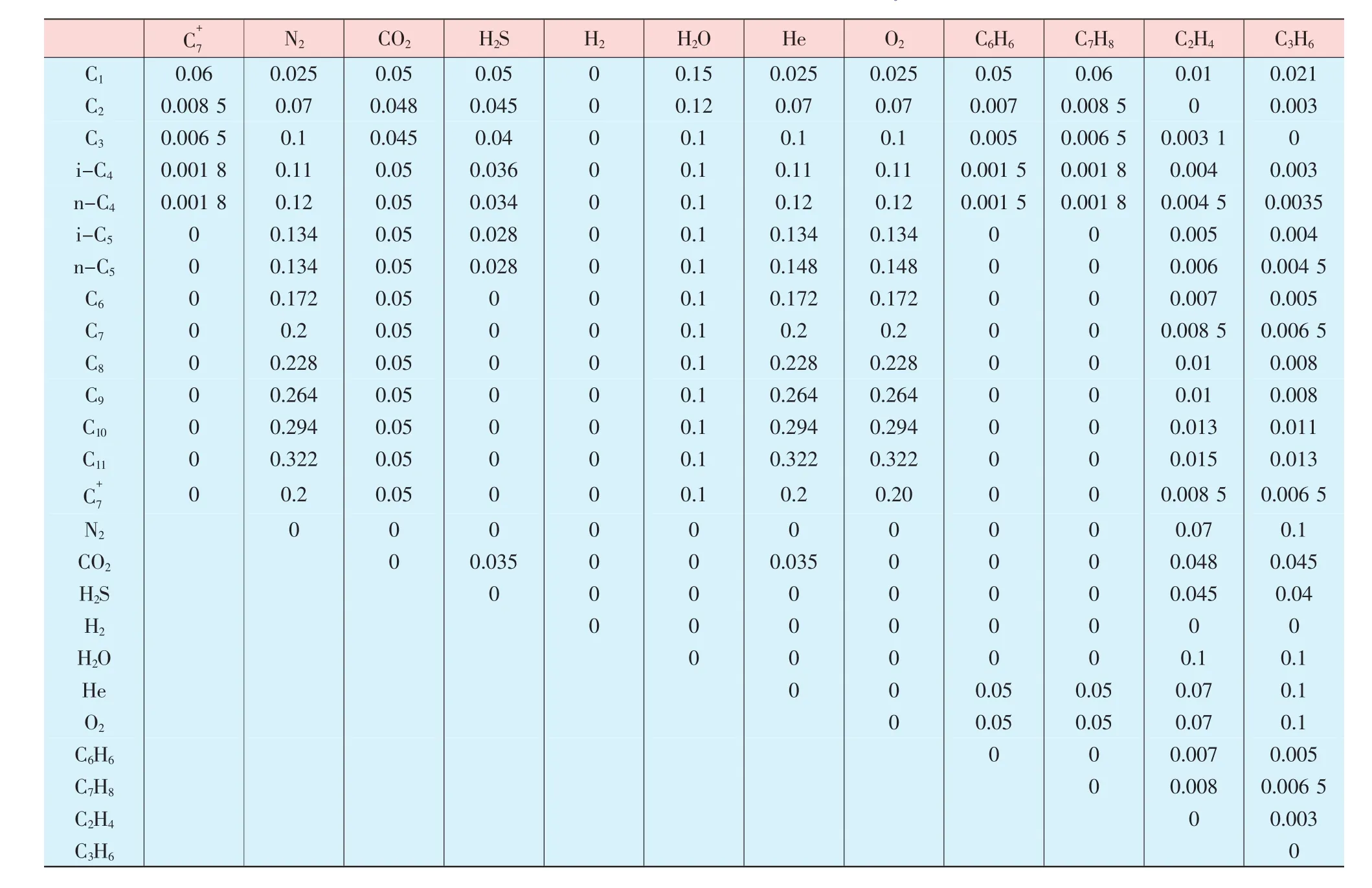
表2 BWRS修改模型中的二元交互作用系数Kij(续)
弦截法求解需设两个初值。
求解气相时:可设ρ1=0,ρ2=
求解液相时:当混合物的偏心因子ωm≤0.24时, ρ1=40.0 kmol/m3(40 mol/L,kg/m3), ρ2=38.0 kmol/m3(38.0 mol/L, kg/m3); 当混合物的偏心因子 ωm> 0.24时, ρ1=20.0 kmol/m3(20 mol/L,kg/m3), ρ2=18.0 kmol/m3(18.0 mol/L, kg/m3)。
迭代到|ρk-ρk-1|≤ε为止,取ε=10-6时,一般迭代次数在6次左右即能收敛。
3.2 压缩因子的求解
当求解出密度后,压缩因子可用下式计算:
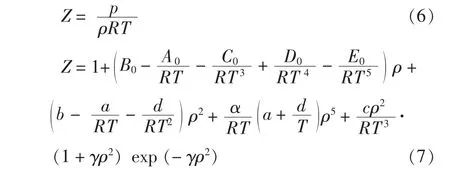
式 (6)和式 (7)计算结果并无差别,推荐使用式 (6), 便于计算[15]。
4 结论
(1)对BWRS状态方程的11个参数进行了改写,将BWRS方程的函数关系转化为无因次的函数关系。使用MBWRS状态方程,可以引入任何一套国际单位制和非国际单位制,计算过程无需单位制转换,避免了管道模拟模型或者其他计算中单位制换算带来的累积误差。
(2)BWRS方程的修正中还包括:引入BWRS新的研究成果,添加了常用组分及其二元交互作用系数。弥补了BWRS状态方程中没有的组分,为更为准确地求得天然气的物性参数提供了有力的保障。
[1]Modisette J L.Equation of State Tutorial[A].PSIG Annual Meeting,2001[C].Salt Lake City:PSIG,2001.
[2]苑伟民,青青,袁宗明,等.输气管道模拟状态方程[J].油气储运,2010,29(3):194-196.
[3]李长俊,汪玉春,陈祖泽,等.天然气管道输送[M].北京:石油工业出版社,2000.
[4]郭天民,阎炜,濮芸辉.多元气液平衡和精馏[M].北京:石油工业出版社,2002.
[5]袁宗明,谢英,梁光川.城市配气[M].北京:石油工业出版社,2004.
[6]姚光镇.输气管道设计与管理[M].山东:石油大学出版社,1991.
[7]吴玉国,陈保东.BWRS方程在天然气物性计算中的应用[J].油气储运,2003,22(10): 16-21.
[8]童景山.流体的热物理性质[M].北京:中国石化出版社,1996.
[9]Gas Processors Suppliers Association.Engineering Data Book[M].Tulsa:GPSA,2004.
[10]苑伟民,孙啸,贺三,等.BWRS方程中参数单位制的讨论[J].长江大学学报(自然科学版), 2008,5(3):179-180.
[11]袁恩熙.工程流体力学[M].北京:石油工业出版社,2002.97-105.
[12]赵汉中.工程流体力学 (I)[M].武汉:华中科技大学出版社,2005.154-161.
[13]苑伟民,袁宗明,贺三,等.输气管网稳态模拟方法研究[J].油气储运,2009,28(10):34-38.
[14]苑伟民,贺三,袁宗明,等.求解BWRS方程中密度根的数值方法[J].天然气与石油,2009,27(1):4-6.
[15]苑伟民,贺三,袁宗明,等.求解BWRS方程中压缩因子的数值方法[J].管道技术与设备,2009,16(3):14-16.
