电性源瞬变电磁响应计算中的误差研究

周楠楠，薛国强，孔祥儒

（中科院矿产资源研究重点实验室，中国科学院地质与地球物理研究所 北京 100029）

0 前言

瞬变电磁法属于时间域电磁感应方法，它利用不接地回线或者接地导线向地下发射阶跃电流，观测由地下介质电磁感应所引起的纯二次场场值。由于观测的是时间域的场值，早期信号反应浅层地电特征，晚期信号到达较晚，反应较深部的地电信息，从而达到测深的目的。电偶源瞬变电磁测深方法采用接地导线源装置，将长接地导线直接作为偶极源处理，观测位于偶极源较远距离处的场值响应［1～5］。

电偶源瞬变电磁测深法具有工作效率高，对地电断面分辨能力强，可以同时弥补频率测深方法探测深度不足，以及MT方法使用天然场为场源的数据不足的缺点。该方法属于深层瞬变电磁测深和回线源的瞬变电磁测深，具有很好的互补性，在煤田、油气田、地热田和地壳深部探测方面有着重要作用［6～12］。

在国际上，陆地和海洋的多道电源瞬变电磁研究，已经取得了重要进展，可为油气勘探中识别油气水和监测液体流动提供重要依据。对电性源瞬变电磁响应进行深入研究非常必要，目前我国也开始筹备电源多道瞬变电磁仪器，准备为研制和使用电性源多道瞬变电磁仪开展资源探测建立试验场地。目前在电偶源场值响应的推导过程中存在大量的近似，这种近似的存在制约着电偶源测深精确测深的发展，因此，我们需要对电偶源测深响应计算中存在的误差进行分析讨论，使我们在使用电偶源测深时对电偶源的数据处理和解释有更加清晰的认识。

作者在本文通过计算，对电性源瞬变电磁响应计算中的理论误差进行研究，研究结果对电性源瞬变电磁法的推广应用具有重要的意义。

1 偶极源本身有长度时的误差

对于电偶极子的定义不是有限长度线源的电荷分布，而是区域分布的概念［13］。理论上，我们在讨论电偶极源的问题时，应该假设源为点源。但在实际的应用中，我们往往以远区条件作为偶极子近似的标准，那么这种近似会带来多大的计算误差呢？我们将以有线长度的天线赤道向上产生的水平电场为例，分析天线长度不为“1”产生的场值及相对应的视电阻率的修正问题。

将记录点设在物探远区场，以保证近似条件的满足，如图1所示，并假设发射天线上的电流是均匀的。

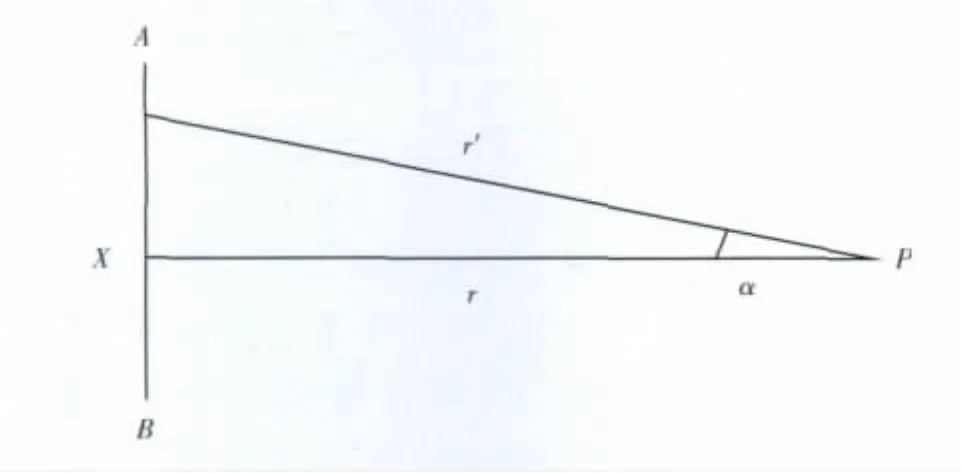
图1 偶极子天线源场值计算示意图Fig.1 Schematic map of dipole antenna

计算赤道向的Ex处理方式是，把发射天线源分为许多地小段，当段数足够多时，对每一小段就可以使用偶极子公式进行计算。设r为发射天线中心点到观测点的距离，r′为天线上某一小段（x，x＋dx）到观测点的距离：

另外，对以该小段来说，观测点也不再是赤道向，其角度为α：

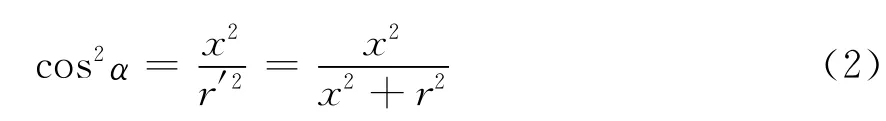
纳米吉安［14］给出了均匀半空间模型下的，平行于电偶极源的电场Ex的表达式（3）。

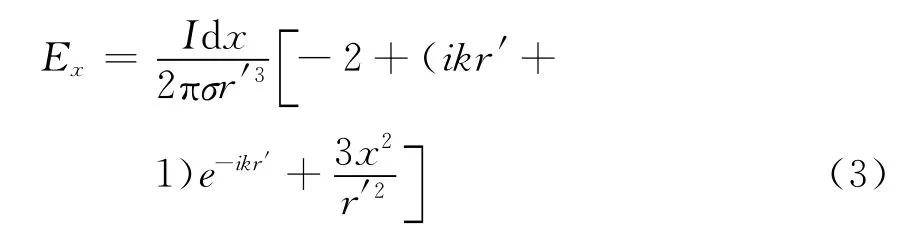
将式（2）代入式（3）中，并运用三角函数关系cos2α＝2cos2α－1，可以得到式（4）。

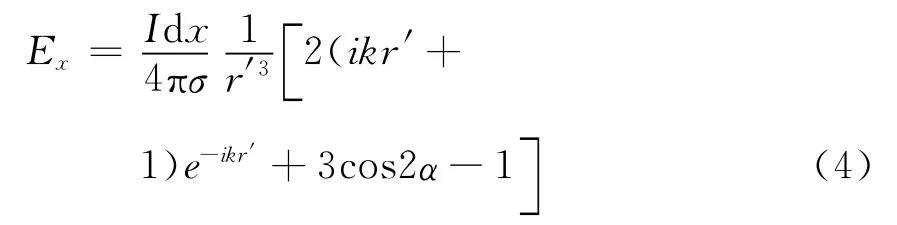
对于层状模型的情况，水平分层情况下的物探远区场的表达式与均匀半空间的模型相似，只是在其中的σ乘上一个因子。

因此，最终我们得到如图1所示的一小段天线在观测点所产生的电场x分量（用dEx表示），可以通过偶极子公式来计算：

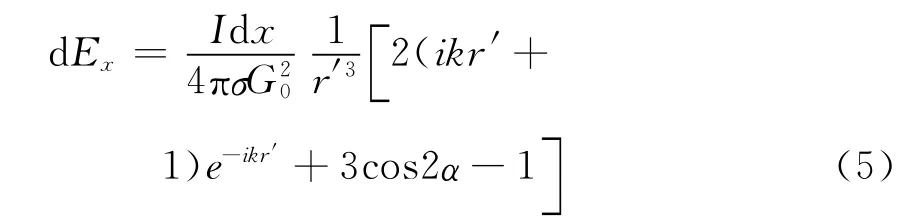
在物探远区｜kr′｜≫1，在式（5）中，含有e－ikr′的项都可以略去，因此得到远区物探场的电场分量的表达式为：

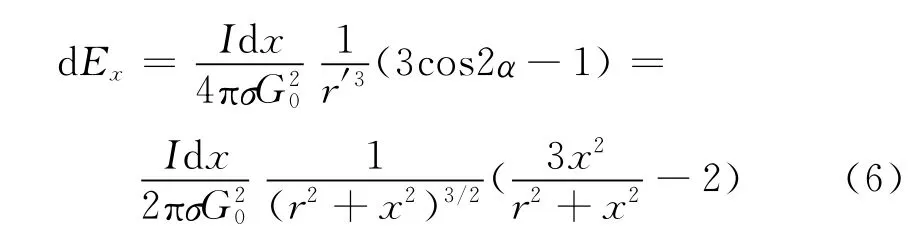
然后，再对各小段产生的场叠加起来，就可以得到总的Ex。当段数无限多时，求和就成为对dx的积分，积分的结果是：

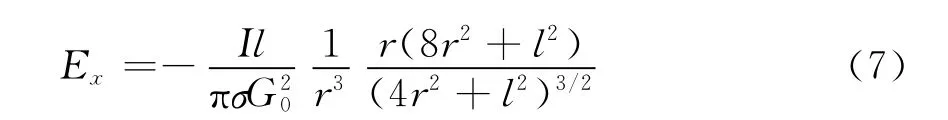
位于中心点的偶极子产生的场为：

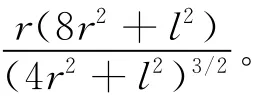
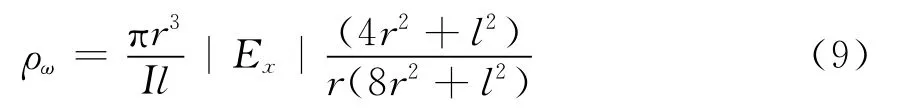
另外，在进行场强测量时，由于接收天线有一长度所测的场不是某一点的值，而是该点附近的平均值，因此需要做一个修正。以物探远区赤道向的Ex为例，设接收天线的长度为l′，同样得到实测的电场¯Ex与接收天线中心点的Ex的关系为：

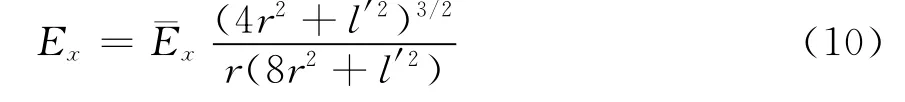
在发射天线和接收天线都比较长时，可以将两个修正因子乘起来，于是在赤道向有式（11）。

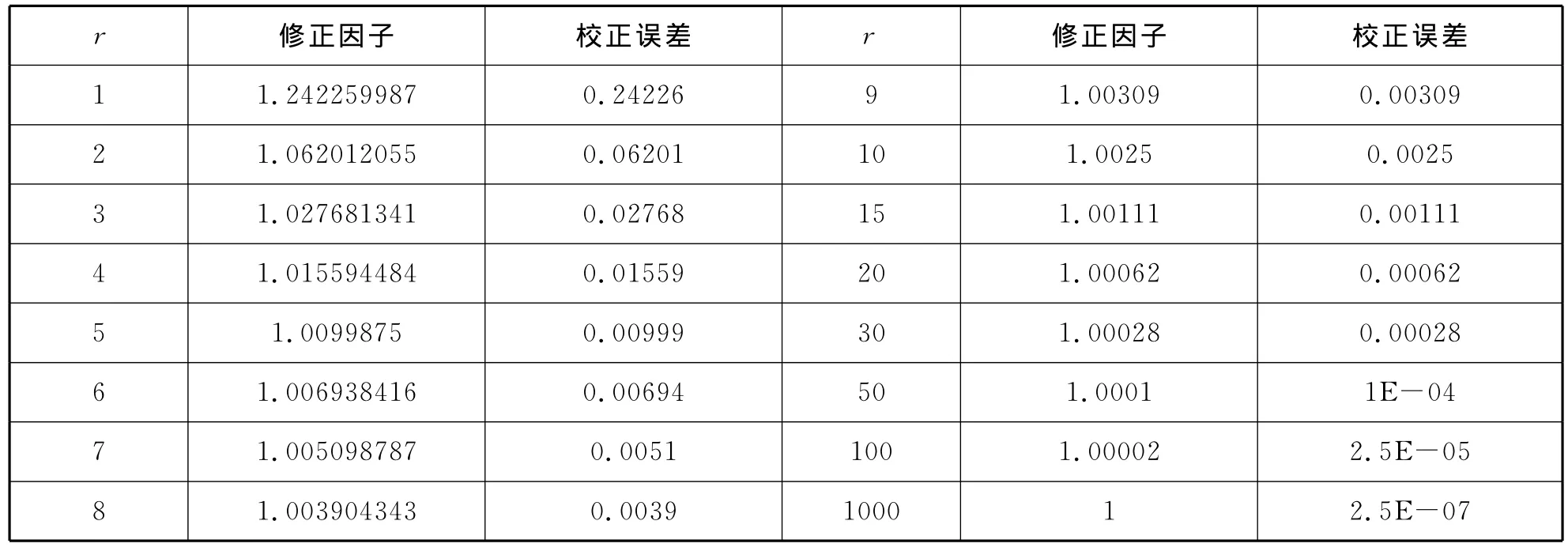
表1 发射长度为“1”时，收发距不断变化引起的视电阻率的校正因子表Tab.1 Correction factor of apparent resistivity for different offset at the length of 1

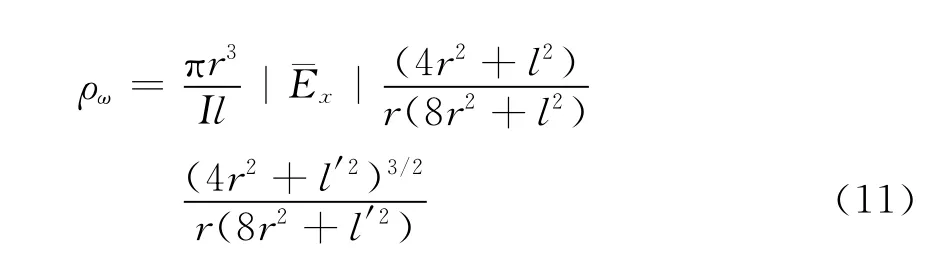
2 均匀半空间频率域场响应计算时的近似

2.1 准静态条件下的位移电流影响

纳米吉安［14］指出在有限源问题中，通常只有发射和接收装置均置于地面，且频率足够低，因而可以采用准静态近似时，才能方便地求得解析解。

在层状介质下的Ex表达式为

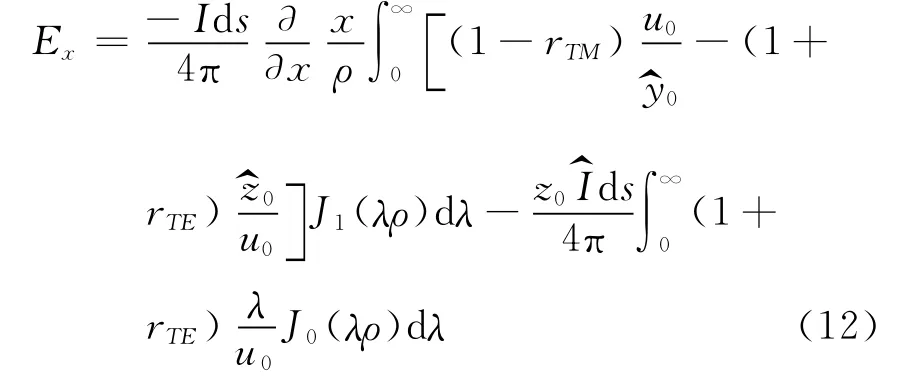
在均匀半空间的介质条件下：

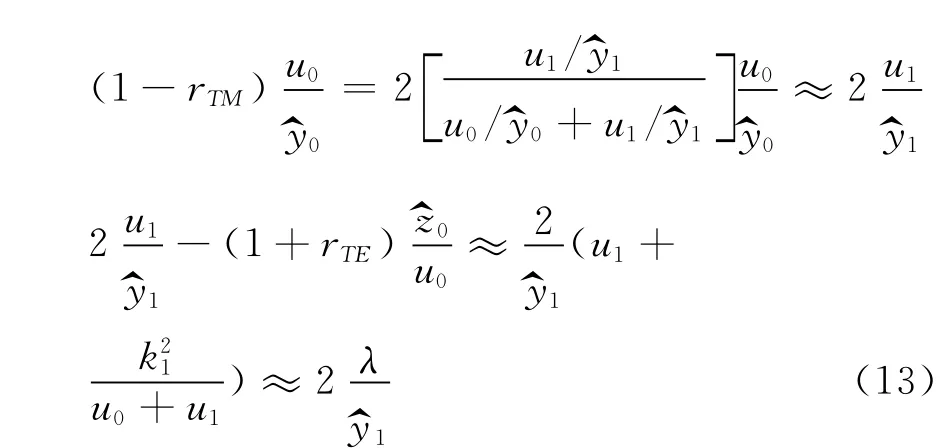
式（13）是在层状介质下的场的表达式，通过准静态近似得到均匀半空间下的场的解，在准静态条件下，忽略位移电流的影响。因此，λ和k1之间存在着近似的对等，这种误差的影响较小，但在理想电介质中这种误差不可忽略。在常见的地质结构中，电导率值相对理想电介质较高，而且电偶源瞬变电磁的发射频率属于低频的范围，远远低于位移电流需要考虑时的高频值。

2.2 比拟过程中的误差分析

为了得到谐变电偶极源的场的特点，往往采用比拟的方法，即将谐变的发射频率设为零，在求频率等于零的均匀半空间表面上，当水平电偶极子形成的电磁场特征时，存在一种假设条件［15］即：

使得原本的均匀半空间介质的频率域的电场径向分量从式（14），在频率等于零时（恒定电流场），简化成式（15）。

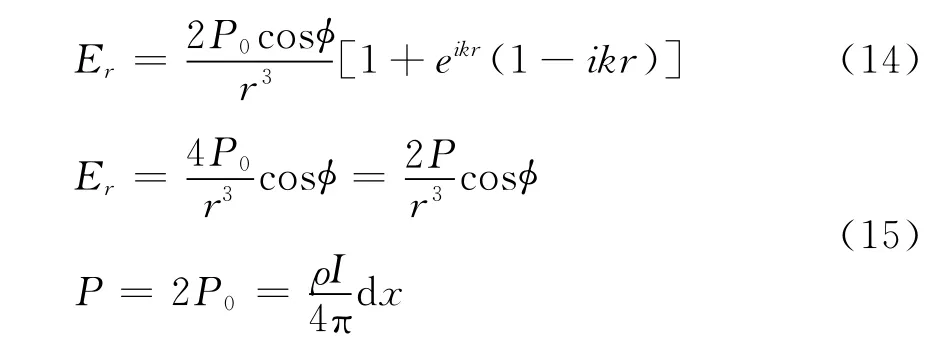
式中 ρ表示均匀半空间的电阻率值。

这种级数的省略带来了一定的计算误差，我们以ex不同阶数的展开式为例进行分析，设x不断变化时，各级数项省略带来的计算误差。

相对误差＝（精确值－各阶次近似）／精确值。所有数值小数点后显示六位有效数字。

表2（见下页）为ex的麦克格林级数展开的不同次数近似的相对误差分析。

2.3 远区勘探近似公式存在的误差分析

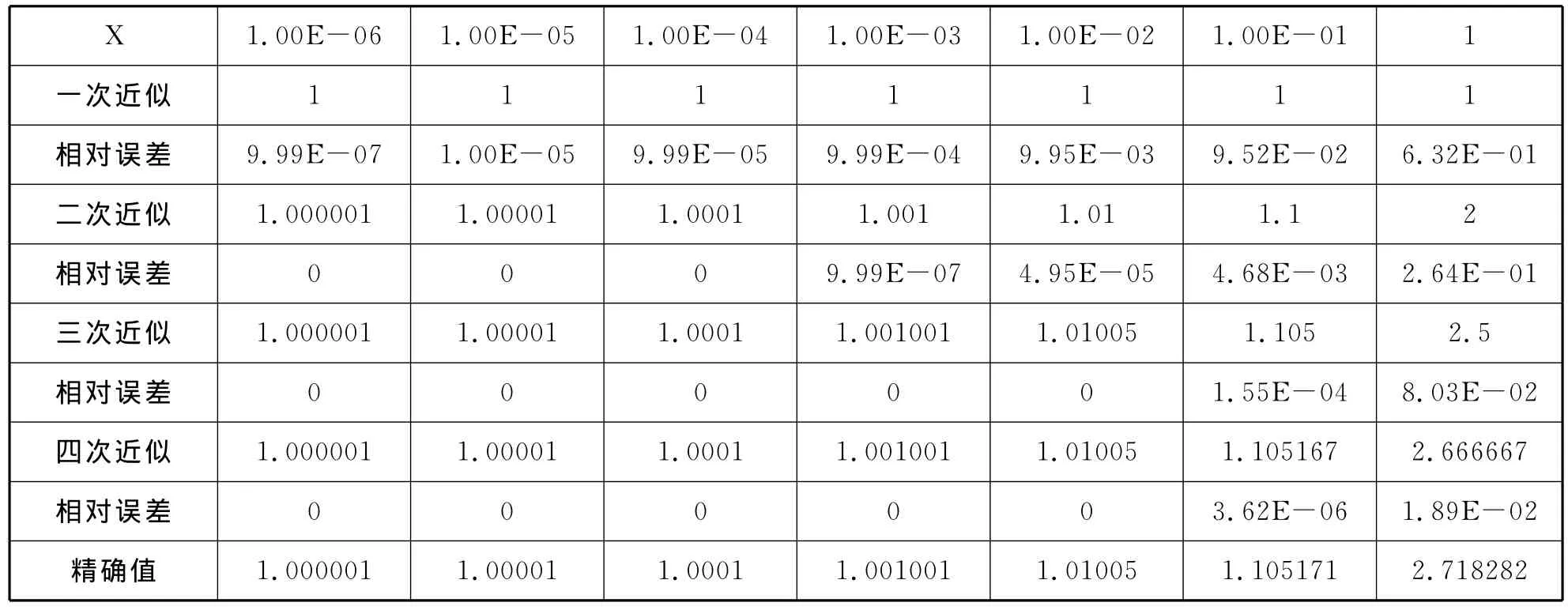
表2 ex的麦克格林级数展开的不同次数近似的相对误差表Tab.2 Relative error for different power at the Maclaurin series

（1）近区：Kr≪1的区域。

（2）远区：Kr≫1的区域。

不论近区和远区，都同时有感应场和辐射场存在，不过若将两者比较起来：在近区感应场较强，辐射场可忽略；在远区，辐射场较强，感应场可以忽略。因而近区主要显现感应场的性质，远区主要显现辐射场的性质。尽管在近区内辐射场比感应场小，但仍比远区的辐射场大很多，否则就会得出离波源越远，辐射场越强的错误结论。实际上，辐射场由近及远随着距离的增加而逐渐衰减。

均匀大地情况水平电偶极子的物探场，理论计算的物探场值为：

在远区，k1r≫1，式（16）中包含eik1r的项略去，则有：

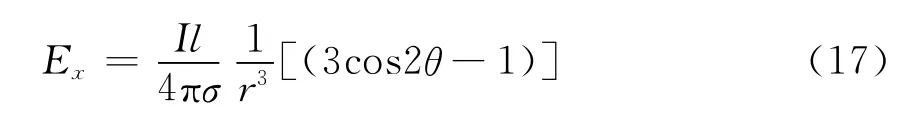
由于在实际使用中的发射频率较低，而且探测区电阻率相对真空小的多，因此，忽略eik1r不会带来较大的相对误差，可以忽略。

3 时间频率域转换的误差存在分析

虽然，在某种条件下频域数据可以转换成时域数据，但就一次场对观测结果的影响而言，两者截然不同。以往先求得频域公式，然后经由频域到时域的转换，利用已有的时域场的结果来研究时域问题，不失为一种重要的方法。但是，有时候很难确定在频率域中采取的哪些近似会对时域影响不大；哪些近似影响较大，可能会掩盖时域最本质的属性。根据因果律，无论何种形式的时间域～频率域转换，都会引起截断误差和混跌计算误差。比如，按照偶极子叠加由频域转换得到的回线源时域解，感应电动势往往在回线边框附近迅速增长，产生奇异。实际上，由于时域中的因果关系，对于以阶跃函数下降沿触发的瞬变场，当电源关断后，在原来的源点处，不会发生奇异，这也是时域瞬变场能够实现频域无法实现的同点装置的原因。在恒定电流场时，偶极源的场解在源点时是奇异的。但我们在野外实际观测的数据是存在的，因为恒定电流场不存在场源的关断，而瞬变电磁法勘探中场源关断后的场解是非奇异的。这也是时间域瞬变电磁测深优于频率域测深的地方。

4 水平层状介质的电偶源场值响应常规计算的误差分析

针对电偶源，一般使用数字滤波等方法进行转换。在转换中存在计算误差，通过分析与解析解的对比，分析误差存在。

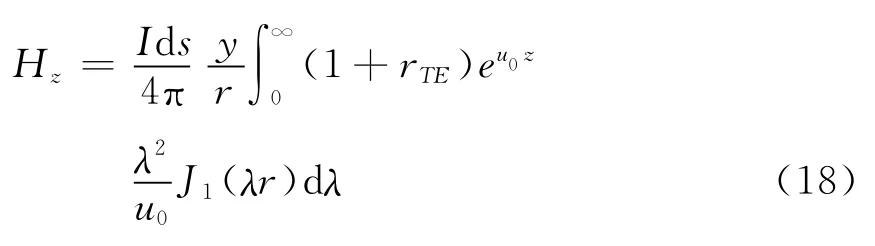
纳米吉安［14］给出层状模型下的水平电偶源的垂直磁场频域解的表达式：其中 I表示激发电流；ds代表偶极源长度；y表示观测点到偶极源的赤道距离；r为收发距；J1（λρ）为一阶贝塞尔函数；λ2＝＋，k0表示波数。

对于N层大地，地表导纳为：

对式（18）进行傅里叶变换式，可得：

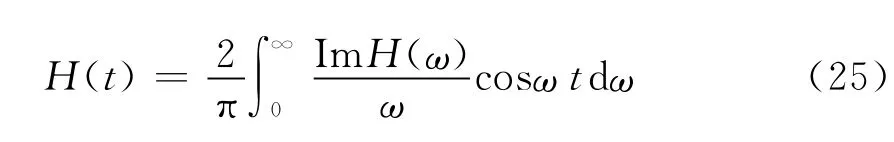
得到时域瞬变电磁场响应公式

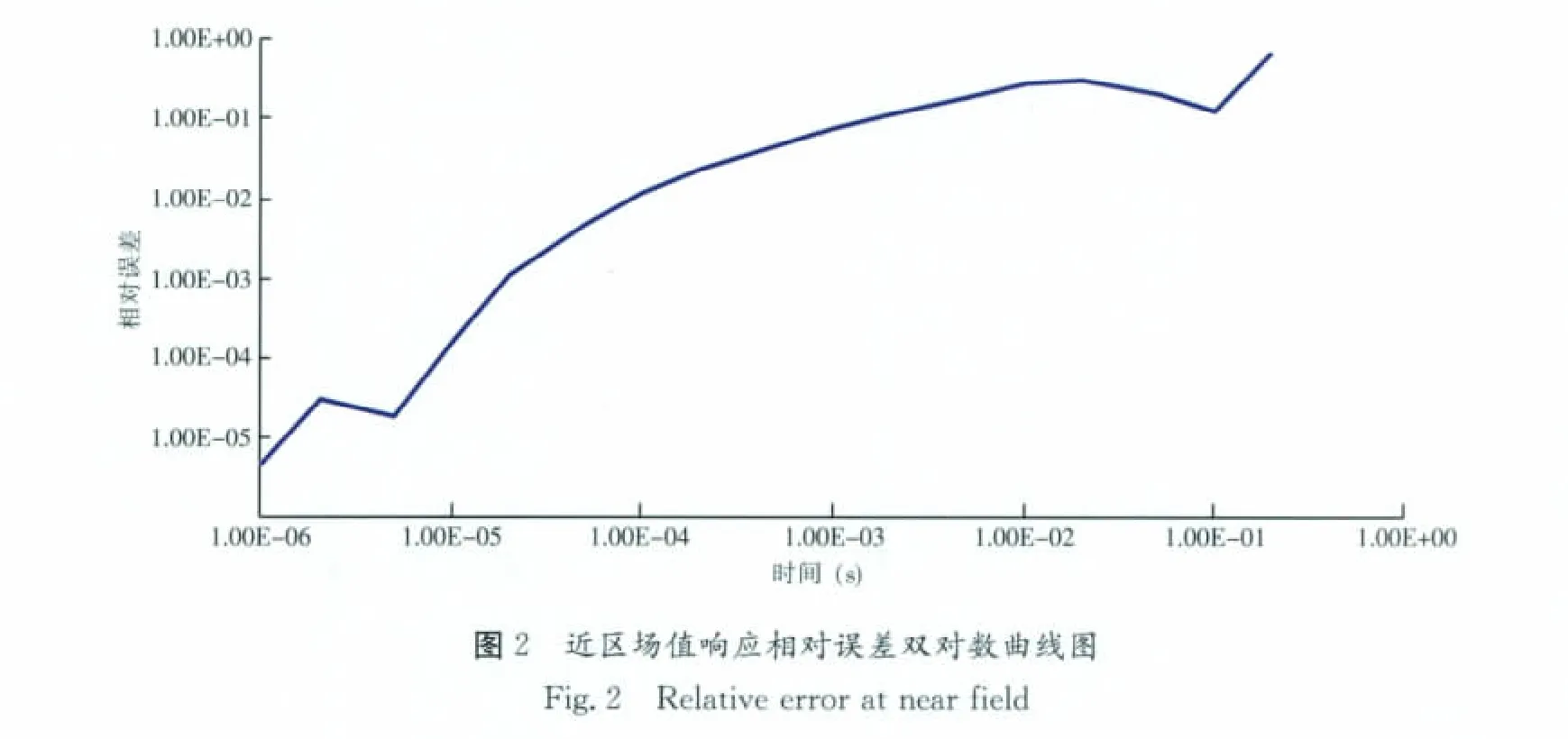
图2为坐标点（0，1）分别使用均匀半空间的精确解和数字滤波方法计算出的场值相对误差曲线。

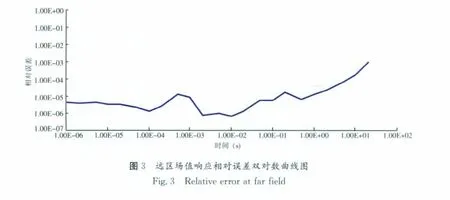
在远区情况下，选取坐标点（0，1000），给出该点的数字滤波方法场值与精确解的相对误差曲线。

通过图2和图3的对比发现，在收发距较小的近区，场值响应使用数字滤波方法求解汉克尔变换和余弦变换时存在一定的计算误差，尤其是在时间较大时。但对于远区点时，在瞬变电磁测深的观测时间范围内，数字滤波的计算偏差可以忽略。以（0，1000）点为例，在10ms时，相对误差只有6.782 97E－07，可以满足野外实际观测的需要。

5 结论

通过上述分析，我们发现在电偶极源瞬变电磁测深的场值响应的推导过程中存在着多处近似，这些近似有的带来较大的计算偏差，如偶极子自身有长度时的误差和数值计算近区场值时相对误差，需要引起我们的注意。同时，在勘探电磁学中，往往需要先在频域中求得稳态场，然后经傅里叶或拉普拉斯变化得到时间域的解这一转换的过程掩盖了因果律，同时在实际的时～频域的变换时带来了计算误差。

尽管瞬变电磁法测深方法和频域场测深方法几乎同时出现，但由于传统的电磁场理论着重研究单一频率的电磁波，直接在时域进行瞬变电磁场研究还属于探索阶段。我们认为有必要寻找一种直接时域求解的方法，以避开频率域求解场值公式时带来的近似和计算偏差。

以时变点电荷为基本单元，不再经过傅里叶或拉普拉斯变换，直接在时间域中推导层状介质表面上的瞬变场解析式，研究时域辅助函数的选取，时变点电荷载流元的处理等，经过一系列处理，分析瞬变场在典型地层和不同场区的响应特征，为瞬变电磁法的进一步发展和实际勘探提供理论基础。

［1］薛国强，李貅，底青云.瞬变电磁理论与应用进展［J］.地球物理学进展，2007，22（4）：1195.

［2］NABIGHIAN M N.Quasi－static transient response of a conducting half－space［J］.Geophysics，1979（44）：1700.

［3］STRACK K M，VOZOFF K.Integrating long－offset transient electromagnetic with seismic in an exploration environment［J］.Geophysical Prospecting，1996，44（6）：997.

［4］陈清礼，严良俊，付志红，等.长偏移距瞬变电磁法全区视电阻率的二分搜索数值算法［J］.石油地球物理勘探，2009，44（6）：779.

［5］方文藻，李予国，李貅.瞬变电磁测深原理［M］.西安：西北工业大学出版社，1993.

［6］BEN K S，JAMES C W，LOUISE P.Correction for the static shift in magnetotelluric using transient electromagnetic souding［J］.Geophysics，1988，53（11）：1459.

［7］严良俊，胡文宝，陈清礼，等.长偏移距瞬变电磁测深法在碳酸盐岩覆盖区落实局部构造的应用效果［J］.地震地质，2001，23（2）：271.

［8］严良俊，王正茂，谢兴兵.表层结构调查中的TEM地形校正［J］.勘探地球物理学进展，2007，30（5）：396.

［9］廖忠，李文尧.线源TEM在腾冲热水塘寻找地热的应用效果［J］.工程勘察，2002，1（2）：67.

［10］吕友生，何展翔.建厂测深在油气勘探中的应用［J］.石油地球物理勘探，1999，34（5）：532.

［11］曹昌祺.水平层状大地的交流视电阻率［J］.地球物理学报，1978，21（3），248.

［12］殷长春，朴化荣.电磁测深法视电阻率定义问题的研究［J］.物探与化探，1991，15（4），290.

［13］吴大猷.理论物理：电磁学［M］.北京：科学出版社，1983.

［14］斯坦利·沃德，杰拉尔德W·霍曼.地球物理用电磁理论［A］.见：米萨克·N纳比吉安主编.勘查地球物理电磁法 第一卷理论［C］.赵经祥，王艳君，译.北京：地质出版社，1992.

［15］A A考夫曼，G V凯勒.频率域和时间域电磁测深［M］，王建谋，译.北京：地质出版社，1987.

［16］周楠楠，薛国强，李梅芳，等.水平电偶源激发的瞬变电磁垂直磁场响应计算与分析［J］.物探化探计算技术，2011，33（增）：88.

［17］李梅芳，薛国强，周楠楠.大回线源瞬变电磁法探测煤矿含水系空区［J］.物探化探计算技术，2011，33（增）：215.