瞬变电磁法对低阻薄层的分辨能力研究
2012-10-29王战军朱自强李建慧鲁光银赵云威彭凌星
王战军,朱自强,李建慧,鲁光银,赵云威,彭凌星
(中南大学 地球科学与信息物理学院,湖南 长沙 410083)
0 前言
瞬变电磁法具有直接观测二次场,近区测量,工作效率高,易穿透高阻覆盖层,对低阻体反应灵敏等优点。目前,瞬变电磁法虽已广泛应用于水文调查,金属矿、煤矿勘探,隧道、巷道超前地质预报中,但瞬变电磁法的资料处理水平并不高。作者在本文将以矩形发射回线中心回线工作装置为例,研究瞬变电磁法对低阻薄层的识别及分辨,探讨瞬变电磁法的探测能力,进而为瞬变电磁法的资料处理解释提供指导。
目前,关于电法及电磁法对地下地质体分辨能力的研究主要有:陈根[1]探讨了偶极和中梯装置反映激电异常的能力;吴英隆等[2]使用直流电测深中的水平层计算软件,研究了对高阻(或者低阻)薄层的有效性探测问题;石显新[3]给出了水平电偶源在地面激发的电磁场各分量表达式,得出了在低频情况下,磁场受低阻覆盖层和水平导电层的影响小的结论;汤井田[4、5]归纳了 MT、CSAMT 对均匀半空间高、低电阻率夹层的分辨能力;安志国等[6]等利用有限元法计算了低阻薄层的电阻率和厚度分别发生变化时的一系列频率——电阻率曲线,归纳了CSAMT法对薄层结构的分辨能力;王艳等[7]通过对三层地电模型的数值模拟研究了如何提高电磁场响应强度,从而研究了CSAMT对深部低阻薄层的分辨能力。
关于瞬变电磁法探测能力研究方面,具有代表性的是:牛之琏[8]讨论了瞬变电磁法对导电层的探测能力;唐新功等[9]以层状介质中两个三维导电薄板为例,计算了距离发送源不同位置的目标体的电磁场响应,但没有分析目标体的厚度发生变化时场的响应规律。Li Xiu[10]等将自适应收缩性遗传算法与视纵向电导微分成像法相结合,提高了瞬变电磁法识别地下薄层的能力。薛国强[11]等通过瞬变电磁法一维响应正演算法,对有无薄层存在的一系列地电模型的视电阻率曲线进行了对比,以相对误差为参数分析了瞬变电磁法对薄层结构体的分辨能力。
1 矩形发射回线激发的瞬变电磁场
作者从垂直磁偶极源激发的频率域电场出发,对其磁矩按回线面积进行积分,推导出了矩形回线源的频率域电场表达式,然后利用14个系数G-S算法得到了时间域电场表达式,根据法拉第电磁感应定律,从电场强度阶跃响应获得了磁场脉冲响应的垂直分量[12、13]。其计算表达式为:
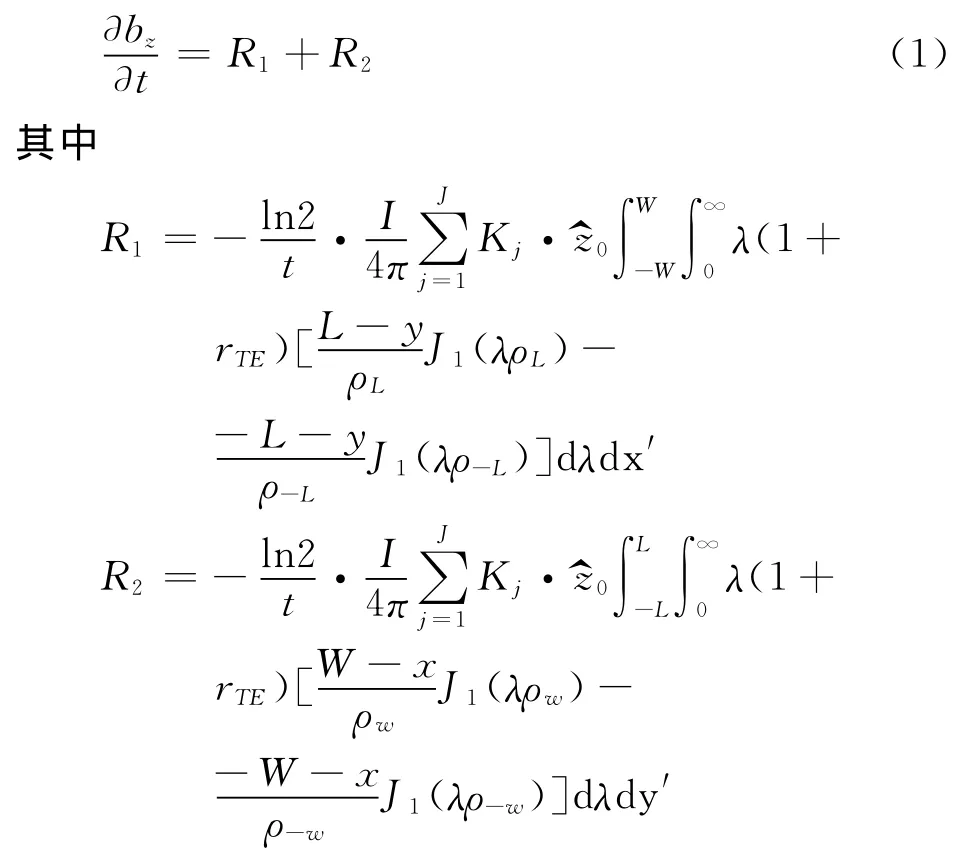
式中 t为时间变量;I为线圈通电电流;Kj是GS算法系数;L和W分别为矩形回线的半边长和半边宽;x、y分别为测点的横、纵坐标;x′和y′分别为矩形线圈内某一小垂直磁偶极源的横坐标和纵坐标;J1为一阶贝赛尔函数;λ为空间波数;=iωμ0(μ0为真空中的磁导率,ω为角频率);ρL=[(x′-x)2+(L-y)2]1/2;ρ-L= [(x′-x)2+(-L-y)2]1/2;ρw= [(W -x)2+(y′-y)2]1/2;ρ-w=[(-W -x)2+(y′-y)2]1/2;rTE为反射系数,由式(2)确定。共有N层;n为序号,表示第n层;μn、εn和σn分别为第n层介质的磁导率、介电常数和电导率。

式(1)是矩形发射回线激发的磁场脉冲响应垂直分量的表达式。由于其含有贝塞尔函数,因此求解式(1)与式(2)时需使用Hankel变换。
2 视电阻率的求取
瞬变电磁法中,视电阻率的定义有晚期视电阻率和全期视电阻率。晚期视电阻率适用于近区晚期情况,并不适用于远区早期。因此在计算早期视电阻率时,往往会出现较大畸变。而作者在本文利用视电阻率来研究瞬变电磁法对低阻薄层的分辨能力,因此需要在所有时刻都能反映真实地电模型的视电阻率定义方法,在此我们采用改进的二分搜索法。
2.1 晚期视电阻率
瞬变电磁场法在近区观测情况下,晚期视电阻率公式可表示为[7]:
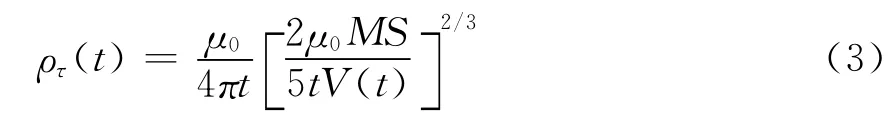
式中 V(t)=-S·∂Bz/∂t,为实测感应电动势;S为接收回线等效面积;M为发射回线磁矩。
2.2 全期视电阻率定义
美国地球物理学家P.Raab和F.Frisehknecht提出:对于均匀半空间,位于地表边长为L的发射回线,其中心处的感应电动势为:
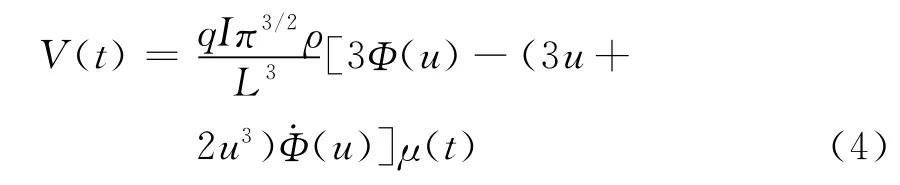
式(4)归一化得核函数为:
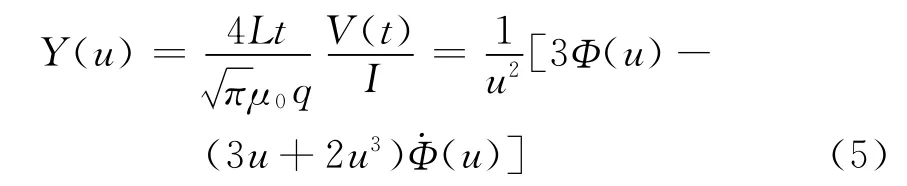
对式(5)求导可知:Y(u)为u的单峰双值函数,并于u=1.613 6处取极大值。因此对于全期视电阻率的求取必然分为三种情况:① 单解;② 双解;③无解。借鉴白登海[15]对全期视电阻率的定义方法:以u=1.613 6作为早晚期的转接点,分段后的函数在各区间均为单调非线性函数。
根据单调函数的一一对应关系,作者在本文采用二分搜索法,并借鉴张成范等[16]求取全期视电阻率的方法估算u值。由于瞬变电磁法勘探具有体积效应,相邻时窗视电阻率值不会突变。因此可利用晚期公式计算最后一个时窗视电阻率,并判断u处于V(t)的上升段或是下降段,从而得出倒数第二个时窗的二分估算区间。依次类推,最终得到全部时窗的视电阻率。
2.3 晚期公式法与改进二分法视电阻率对比
由图1(见下页)可知,利用晚期公式计算的视电阻率,在早期出现畸变,偏大于地电模型真实电阻率。而利用改进二分法可以求解出所有时刻精确的视电阻率,均反映了地电模型的真实电阻率。另外,由于一维正演程序在晚期精度较差,特别是在均匀半空间电阻率较大时,感应电动势精度就会降低,从而导致在晚期视电阻率精度的下降(见图1)。

图1 改进二分法与晚期公式法视电阻率对比图Fig.1 Comparison diagram of apparent resistivity for improved dichotomy and advanced formula
3 低阻薄层的分辨能力研究
作者在本文的研究思路为:首先利用回线源的一维正演公式计算出不同地电模型的感应电动势;并利用改进二分法计算全期视电阻率;再计算该地电模型与均匀半空间地电模型的视电阻率差值百分比,其计算方法见式(6)。
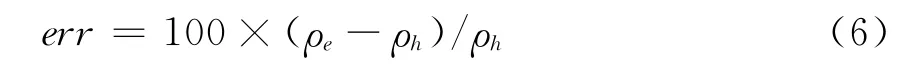
式中 ρe为实际地电模型全期视电阻率;ρh为均匀半空间地电模型电阻率。最后,以err来分析瞬变电磁法对低阻薄层的分辨能力。
我们以三层地电模型作为研究对象。第二层(中间薄层)作为低阻异常体,第一层和第三层作为围岩。①当埋深厚度比为1∶5时,埋深分别为100m及200m,薄层与围岩视电阻率差异为1∶1.2、1∶1.5、1∶2时的瞬变电磁响应曲线;②当埋深厚度比为1∶10时:埋深分别为100m及200m,薄层与围岩视电阻率差异为1∶1.5、1∶2、1∶4时的瞬变电磁响应曲线;③当埋深厚度比为1∶20时:埋深分别为100m及200m,薄层与围岩视电阻率差异为1∶1.5、1∶2、1∶4时的瞬变电磁响应曲线。
围岩电阻率为50Ω·m和100Ω·m时,模型参数为:发送回线边长100m,接收回线边长10m,发送电流10A,观测时间范围为0.05ms~20ms。考虑到一维正演计算精度问题,当围岩电阻率为200Ω·m时,所用发送回线边长改为200m,其它参数不变。
3.1 埋深厚度比为1∶5时地电模型
由下页图2可以看出,随着薄层与围岩电阻率差异比值的减小,视电阻率曲线由趋于平缓逐渐凹陷,至视电阻率差异比为1∶2时,曲线凹陷最为明显并呈倒S形态,并且曲线的最大异常值随围岩电阻率的增大呈现向早期移动的趋势。对比图2(a)及图2(d)、图2(b)及图2(e)、图2(c)及图2(f)可知,随着薄层埋深的增加,电磁波在顶层的传播时间延长,视电阻率异常极值出现明显滞后。通过分析图2模型视电阻率值可知,当薄层埋深厚度比为1∶5时:埋深分别为100m及200m、薄层与围岩电阻率差异为1∶2时,err极大值均略小于10%,即为分辨极限。另外,当围岩电阻率大于100Ω·m时,曲线晚期段出现震荡,导致异常反映不明显。
3.2 埋深厚度比为1∶10时地电模型
由后面图3可以看出,曲线形态与图2呈现相同形态及变化规律,但当电阻率差异比值大于1∶2时,曲线总体趋于平缓,异常反映不明显。对比图3(a)及 图3(d)、图3(b)及 图3(e)、图3(c)及图3(f)可知,随着薄层埋深的增加,视电阻率异常极值出现滞后比图1更为明显。通过分析图3模型视电阻率值可知,当薄层埋深厚度比为1∶10时,埋深分别为100m及200m、薄层与围岩电阻率差异比为1∶2时,err极大值均小于10%,认为不可分辨;而电阻率差异比为1∶4时,err极大值大于10%,故可认为分辨极限。
3.3 埋深厚度比为1∶20时地电模型
由后面图4可以看出,曲线形态与图2呈现相同形态及变化规律,但视电阻率曲线总体趋于平缓,除电阻率差异比为1∶4外无特别明显异常。对比图4(a)及图4(d)、图4(b)及图4(e)、图4(c)及图4(f)可知,随着薄层埋深的增加,视电阻率异常极值出现明显滞后。对图4模型视电阻率值分析可知,当薄层埋深厚度比为1∶20时,埋深分别为100m及200m、薄层与围岩电阻率差异比为1∶4时,err极大值均略小于10%,即为分辨极限。
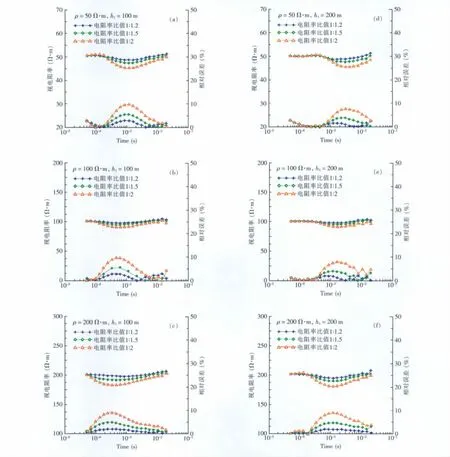
图2 埋深厚度比为1∶5时模型视电阻率曲线Fig.2 The curves of apparent resistivity when the ratio of depth and thickness is 1∶5
4 结论
从瞬变电磁法数值模拟层面来讲,其对于薄层的探测能力与薄层的埋深厚度比,以及围岩电阻率差异比等因素有关。本文作者以三层地电模型为例,深入探讨了瞬变电磁法对低阻薄层的分辨能力,并得到以下结论:
(1)随着薄层与围岩电阻率差异比值的减小,视电阻率曲线异常极大值随围岩电阻率的增大,呈现向早期移动的趋势;而随着薄层的埋深的增加,视电阻率曲线异常极大值向晚期滞后。因此对于视电阻率曲线的异常形态应加以综合评判,以确定这一异常是由薄层电阻率值的变化还是由厚度的变化引起的。
(2)瞬变电磁法能有效探测低阻薄层:当薄层埋深厚度比为1∶5时,薄层与围岩电阻率差异比1∶2可以作为分辨极限;当薄层埋深厚度比为1∶10时,薄层与围岩电阻率差异比为1∶4可以分辨;而当薄层埋深厚度比为1∶20时,薄层与围岩电阻率差异比1∶4可作为分辨极限。

图3 埋深厚度比为1∶10时模型视电阻率曲线Fig.3 The curves of apparent resistivity when the ratio of depth and thickness is 1∶10

图4 埋深厚度比为1∶20时模型视电阻率曲线Fig.4 The curves of apparent resistivity when the ratio of depth and thickness is 1∶20
[1]陈根.偶极装置反映激电异常的能力[J].物探与化探,1986,10(5):398.
[2]吴英隆.直流电测深对高阻和低阻薄层的探测能力[J].桂林冶金地质学院学报,1994,14(2):174.
[3]石显新.水平电偶源充电电磁法正常场研究及其应用[J].煤田地质与勘探,1996,24(2):42.
[4]汤井田,何继善.可控源音频大地电磁法及其应用[M].长沙:中南大学出版社,2005.
[5]汤井田,周聪,邓小红.CSAMT视电阻率曲线对水平层状大地的识别与分析[J].地质与勘探,2010,46(6):1079.
[6]安志国,底青云.CSAMT法对低阻薄层结构分辨能力的探讨[J].地震地磁观测与研究,2006,27(2):32.
[7]王艳,林君,周逢道,等.CSAMT法深部低阻分辨能力及方法研究[J].中国矿业大学学报,2009,38(1):86.
[8]牛之琏.瞬变电磁测深法对导电层的探测能力[J].地质与勘探,1992,28(7):37.
[9]唐新功,胡文宝,严良俊.瞬变电磁法对地下不同位置多个三维薄板探测能力的研究[J].物探与化探,2004,28(6):528.
[10]LI XIU,XUE GUOQIANG,SONG JIANPING,et al.Application of the Adaptive Shrinkage Genetic Algorithm in the Feasible Region to TEM Conductive Thin Layer Inversion[J].Applied Geophysics,2005,2(4):204.
[11]薛国强,邓湘.瞬变电磁法对薄层的探测能力[J].石油地球物理勘探,2007,42(6):709.
[12]米萨克N纳比吉安.勘察地球物理电磁法第一卷理论[M].赵经祥,王艳君,译,北京:地质出版社,1992.
[13]李建慧,刘树才,朱自强,等.矩形回线激发的电磁场与磁场的对称关系研究[J].中南大学学报:自然科学版,2010,41(2):638.
[14]李建慧,朱自强,刘树才,等.基于Gaver-Stehfest算法的矩形发射回线激发的瞬变电磁场[J].石油地球物理勘探,2011,46(3):489.
[15]白登海,MAXWELL A MEJU,卢健,等.时间域瞬变电磁法中心回线方式全程视电阻率的数值计算[J].地球物理学报,2003,46(5):698.
[16]张成范,翁爱华,孙世栋,等.计算矩形大定源回线瞬变电磁测深全区视电阻率[J].吉林大学学报:地球科学版,2009,39(4):755.
