隧道开挖释放荷载的有限元模拟方法研究
2012-10-27陶星
陶 星
(中铁二院工程集团有限责任公司地下铁道设计研究院,四川成都610031)
隧道工程区别于其它建筑工程的特点之一是其不断地开挖和支护,对开挖的模拟是隧道数值分析中的重要问题之一。从理论上讲,隧道的开挖模拟是三维空间黏弹塑性问题,但是由于三维分析工作量巨大,要花费大量的时间进行前后处理和数值计算,因此,往往将其简化为平面应变问题,采用二维分析方法,此时,工作量将成倍减少,容易被工程技术人员掌握,且在正确的模型和边界条件下也可得到满意的结果。
在二维分析中,为了模拟掌子面的空间支护效应,多采用应力释放法进行分析,而释放荷载的选取对计算结果有重要影响。尽管采用有限元方法进行隧道数值分析已有很长的时间,也积累了很多的经验,但是对软件的理解和操作不当,经常会得出错误的结论。本文针对隧道开挖释放荷载的模拟方法进行了对比总结,为正确使用软件进行隧道开挖模拟提供科学依据。
1 几种开挖释放荷载的计算方法
1.1 Mana[1]法
所谓开挖释放荷载实际上是被开挖掉的那部分单元通过开挖界面与剩下的单元之间的相互作用力,因此在开挖前它在本质上是内力。每一次开挖使得所暴露出来的表面为自由表面,即无应力状态,此时,需要将相互作用力反方向施加在开挖剩余体系上。
记被开挖掉的那部分单元的全体为ΩE,SE是开挖边界,作用在ΩE上的外载除了SE上的面力荷载p(开挖荷载)外,还有体积力b(自重或渗流力),由它们产生的内力σ,因此有
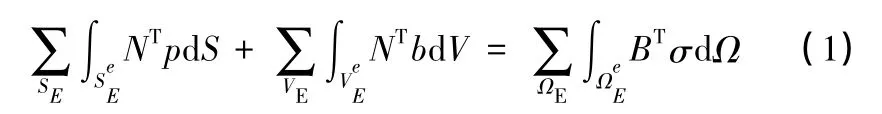
上式第一项即为开挖引起的等效节点力fE,因此
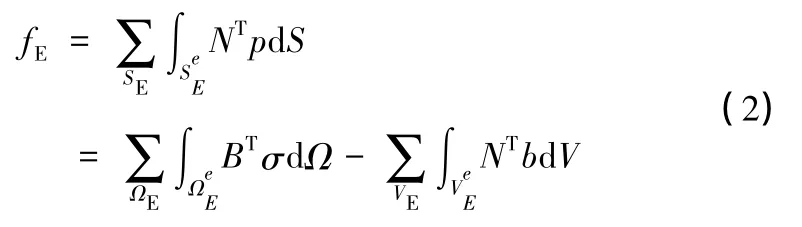
但目前大多数有限元程序给出的开挖荷载仅含上式右边的第一项,也就是Mana提出的应力直接积分法。实际上这是不对的[2],例如b是密度时,传统的计算方法就未计入重力对开挖荷载的贡献。由于开挖往往引起卸荷破坏,因此传统的计算方法可能会低估破坏区,且开挖体的埋深越浅,所引起的偏差就越大。
在隧道开挖模拟过程中,先进行初始应力计算,然后根据Mana公式计算释放荷载,在除去开挖体的结构上向洞内施加(反转应力)等效节点力,计算应力增量和位移增量,然后叠加初始应力场得到二次应力场,位移增量为开挖引起的扰动位移,具体过程见图1。
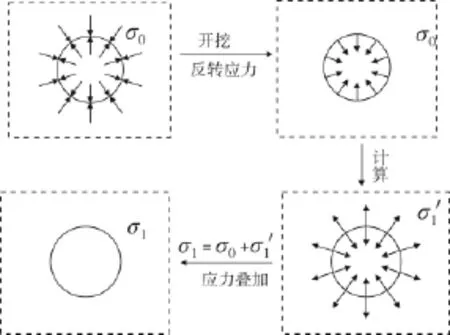
图1 开挖释放荷载计算过程
1.2 刚度折减法
此法由Swoboda教授[3]提出,也称刚度逐步软化法,即对开挖单元的弹性模量乘以一个软化系数α,模拟应力逐步释放,在衬砌施工完成后,开挖单元的弹性模量为零,具体过程见图2。
此法虽没有严格的理论基础,软化系数的选取带有很大的任意性,但是易于在通用有限元程序中实现,如果能结合现场测试结果,确定每次施工合理的软化系数,不失为一种很好的模拟方法。
1.3 支撑荷载法
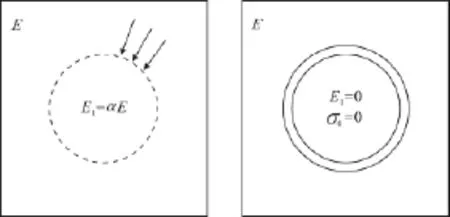
图2 刚度折减法原理
隧道的开挖打破了开挖边界上各点的初始平衡状态,开挖边界上的节点力不平衡,会产生新的变形,引起应力重分布。此时可以“杀死”开挖单元,即开挖单元具有“零应变”状态,为了克服方程的病态性,将开挖单元的刚度乘以一个很小的系数,同时约束位移。此时,可在上一步的基础上继续进行求解,应力状态自动进行叠加,位移需减去初始状态。上述方法称为“地应力自动释放法”,也是目前通用有限元程序采用“生死单元”模拟开挖的方法。如果在开挖边界上施加虚拟的支撑力,来模拟围岩的逐步卸载,就是支撑荷载法[4]。文献[5]详细讨论了支撑荷载的作用方向、选取方式及释放系数的取值,不再赘述。
支撑荷载和释放荷载作用方向相反,且有如下关系,设每一步开挖的荷载释放系数为αi,第n步开挖的释放荷载为αnfi,则支撑荷载为:
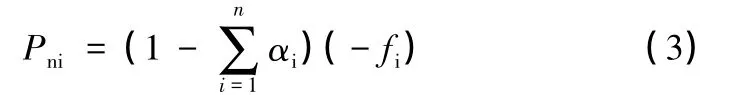
对于分布开挖,可按上式分布施加支撑节点力,具体见图3。
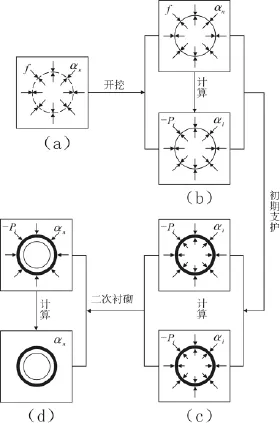
图3 支撑荷载法计算过程
2 从体系平衡观点看释放荷载计算
在数值计算中,可以从两种角度分析开挖对体系的作用。
(1)开挖解除了卸载部分对剩余部分的作用力,使剩余部分失去平衡,所以可对卸载部分对剩余部分的作用力进行分析,也就是对卸载部分进行分析,具体实现方式就是开挖释放荷载的计算(Mana法等),这种思路称为开挖的间接分析。
(2)任一时刻,体系保持平衡或者失去平衡都是体系内力和外力共同作用的结果,开挖将卸载部分的内力转化为剩余部分的外力,故可以对剩余部分进行分析,完全放弃释放荷载的概念,更容易保证分析的可靠性,这种思路称为开挖的直接分析,支撑荷载法和软化刚度法都属于这种思路。
可以从体系平衡的有限元数值格式上证明,这两种方法是等价的,但实现的难易程度是不同的。
3 结论
本文总结了隧道开挖释放荷载的有限元模拟方法,从开挖分析的间接和直接分析思路得出几点结论:
(1)Mana法是一种间接计算开挖作用的分析方法,计算繁琐,经常需要自己编程计算等效节点力,且忽视体积力的影响,不适宜采用通用有限元软件分析。
(2)刚度折减法没有严格的理论依据,软化系数的选取带有很大的任意性,但最容易在通用有限元程序中实现。
(3)支撑荷载法是一种直接考虑开挖作用的分析方法,理论严密、概念清晰,比较容易在通用有限元程序中实现,且计算过程应力场和位移场自动叠加,非常适合多施工步开挖的模拟。
[1]Mana A I,Clough G W.Predicition of movement for braced cuts in clay[J].Geotechnical Engrg Division,1981,107:759-778
[2]郑宏,葛修润,谷先荣,等.关于岩土工程有限元分析中的若干问题[J].岩土力学,1995,16(3):7-11
[3]SWOBODA G,EBNER H,WANG S J,ZHANG J M.Application of the decoupled finite element analysis in tunneling[A].Numerical Methods in Geomechanics[C].Rotterdam:Balkema,1988:1465-1472
[4]孙均.地下工程设计理论与实践[M].上海:上海科学技术出版社,1996
[5]高峰,孙常新.隧道开挖模拟的支撑荷载法研究[J].中国公路学报,2010,23(4)
