微波暗室内静区的功率比计算模型

2012-10-27杨春峰叶文超

沈阳大学学报(自然科学版) 2012年5期

杨春峰，杨敏，叶文超

（沈阳大学建筑工程学院，辽宁沈阳 110044）

为了研制高效吸波的特殊材料，将吸波材料设计成合理的形状使之发挥最大效能等，这样的测试与仿真，常放置在被称为“无回波暗室”的实验室中进行.而设计满足仿真技术要求的微波暗室是实验的前提，静区性能又是微波暗室综合性能的体现，也是暗室设计的关键，且静区从诸墙面得到的反射信号的功率之和与从信号源直接得到的微波功率之比可以作为其判断依据.目前，常常通过电平的试验结果去评价微波暗室是否满足仿真要求，而本文基于模拟目标运动的原理和光学原理，从数学建模角度，推导出了功率比的理论计算公式.

1 研究思路

为了分析微波暗室问题，利用几何光学方法对矩形微波暗室静区性能进行分析.通过控制相邻两天线的辐射强度成比例的变化，运用等价重心原理，模拟了15个视在目标点的相对连续运动.应用光学镜像原理，分析了微波从“发射点→墙面反射区→静区”传播过程.依据“辐射功率＝辐射通量＝辐射强度×立体角”的理论公式，建立了静区从诸墙面得到的反射信号的功率之和与从信号源直接得到的微波功率之比的数学模型.根据发射点、墙面反射区、静区的反射的几何关系，把微波的功率比转换为发射点到墙面反射区中心点的距离、发射点到静区中心点的距离、墙面反射中心点到静区中心点的距离之间的关系.

2 微波静区内功率比的数学模型建立

2.1 微波暗室的基本构造

一种已经研究成功的仿真系统主要由目标模拟器系统、作为导引头支架的三轴转台和微波暗室组成，如图1所示.目标模拟器用来模拟目标运动，它由天线阵列子系统及其控制子系统组成.天线阵列是安置在微波暗室靠近一面墙、有规律排列在同一球面的若干个微波天线，各天线的中心轴线对准球心，按某种规律依次发射模拟目标回波的微波信号，模拟自由空间中目标相对于导弹的运动.需要测试的导引头安装在三轴转台上，转台根据导引头跟踪目标时发出的制导指令作三自由度角度的转动，带动导引头模拟导弹在空间的三自由度运动.微波暗室提供一个微波“自由空间”［1］.

设暗室的宽为B，高为H，长为L，线阵列的圆弧半径为R，目标模拟器对导引头的总张角为β，所有墙面铺设同一规格的吸波体，暗室右端中心的s×s的小方块面积处是安置导引头的部位，称为“静区”.静区小方块的中心点与目标模拟阵列圆弧的圆心重合.同时建立如图1所示的坐标系.

图1 微波暗室基本构造Fig.1 The basic structure of the microwave darkroom

2.2 视在目标点的运动轨迹

2.2.1 视在目标离静区中心点的距离

依据等效重心原理，假定天线信号发出的辐射强度依次为I0，kI0，k2I0，…，k15I0，如图2所示.依据视在目标功率的大小模拟了导弹与目标之间距离的远近，可得式（1）.

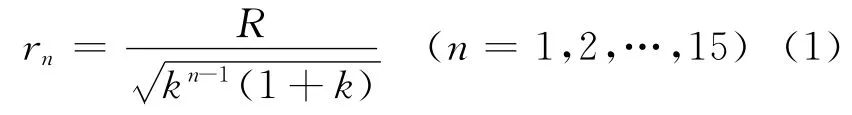
图2 视在运动目标运动过程示意图Fig.2 Moving process diagram installed target

式中，rn为第n个视在目标点离静区中心点的距离，R为线阵列的圆弧半径，k为常系数.

2.2.2 视在方向的确定

由几何关系可推得式（2）和式（3），

当k≤1时，

式中，αn为第n个视在目标点的视在方向与oy轴的夹角，β为目标模拟器对导引头的总张角，β0为相邻两天线的夹角.

2.2.3 视在目标点坐标的确定

根据几何关系可以得出式（4）和式（5），

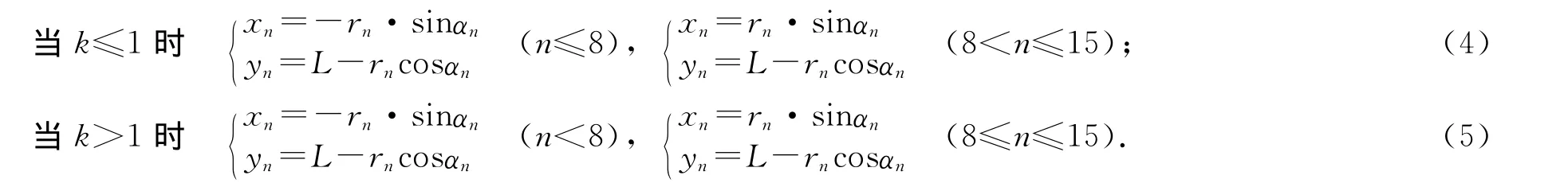
式中，xn为第n个视在目标点的横坐标，yn为第n个视在目标点的纵坐标，L为暗室的长度尺寸.

4～6岁儿童处于前运算阶段(2～7岁)，已经建立了符号功能，能凭借象征性符号进行思维，即可以形成一定的概念，但是，由于掌握的词语、语句还比较匮乏，尚未形成类概念(明玉君，2009)。这意味着4～6岁的儿童能够有基本的死亡概念，但可能在某些维度上发展并不成熟。考察儿童对死亡的无功能性的理解情况，即儿童来生信念的特点，能反映儿童对死亡认知的水平及朴素生物学的理解。

2.3 墙面反射区域的确定

2.3.1 视在目标点的像点坐标

根据镜像原理［2］，如图3所示.对于平行yoz平面的其中一个墙面x＝B／2，此时像点x′n＝B-xn，y′n＝yn；另一墙面x＝-B／2，此时像点x′n＝-B-xn，y′n＝yn.对于平行xoy平面的其中一个墙面z＝H／2，此时像点y′n＝yn，z′n＝H；另一墙面z＝-H／2，此时像点y′n＝yn，z′n＝-H；平行zox平面的墙面，y＝0，此时像点x′n＝xn，y′n＝-yn.

2.3.2 墙面反射区域中心点坐标的确定

像点（B-xn，yn），静区中心点（0，L），此时两点的连线方程为：y＝·x＋L，与墙面的交点；像点（-B-），静区中心点（0，L），此时两点的连线方程为：y＝·x ＋L，与墙面的交点像点（，H），静区中心点（L，0），此时两点的连线方程为-L），与墙面的交点像点，-H），静区中心点（L，0），此时两点的连线方程为：z＝· （y-L），与墙面的交点；像点（），静区中心点（0，L），此时两点的连线方程为与墙面的交点

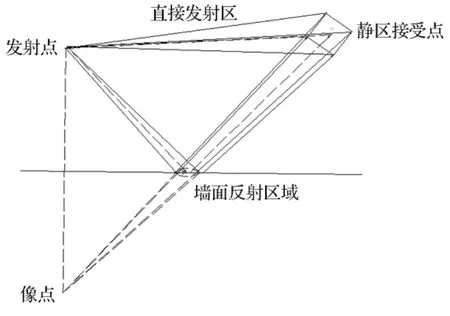
图3 微波传播过程示意图Fig.3 Microwave propagation diagram

2.4 静区内功率比的数学模型

2.4.1 发射点与反射中心的距离ri1和反射中心与静区中心的距离ri2的计算

对于平行yoz平面的墙面、平行xoy平面的墙面和平行xoz平面的墙面，当已知两点坐标时，可推得其之间的距离计算公式分别如式（6）～式（8）所示，

式中，xni，yni分别为平行yoz墙面的像点与静区中心点连线在墙面的交点横、纵坐标；

式中，xni，yni分别为平行xoz墙面的像点与静区中心点连线在墙面的交点横、纵坐标.

2.4.2 功率比值的计算

依据辐射功率的定义［3-4］，即辐射功率等于辐射强度与立体角的乘积，可推得第n个视在目标点在静区内的功率比γn，计算公式如式（9）所示.

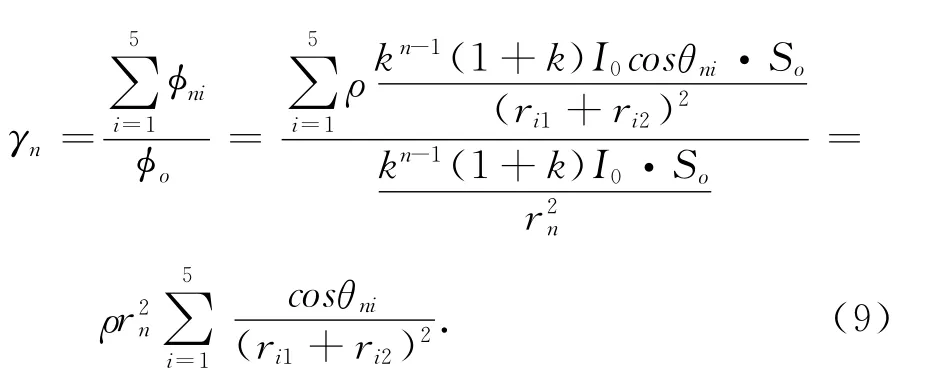
式中，φni为第n个视在目标点在静区内从第i个墙面得到的反射信号的功率，φo为第n个视在目标点在静区内从信号源直接得到的微波功率，ρ为垂直反射率，So为静区面积，cosθni为第n个视在目标点经第i个墙面反射的到静区的电磁波与法线方向夹角的余弦值.

3 实例计算

设暗室的宽B＝18m，高H＝14m，长L＝15 m，b＝1m，线阵列的圆弧半径R＝14m，s＝0.3 m，且目标模拟器对导引头的总张角β＝45°，每3°安装一个天线，共16个天线.目标模拟器对导引头的视在目标运动从左端开始，以匀角速运动到右端，前后共4s，视在天线中心轴线对准静区中心，中心轴线处的发射功率强度随时间线性增大，结束时比初始时增大了一倍.并做出如下假设：①视在天线发射功率强度分布满足余弦辐射体；②只考虑所有墙面对辐射的反射，不计入墙面的散射；③不计入模拟器的天线及其安装支架以及导引头本身对辐射的影响；④天线发射的反射波是同频率同相位且相同极化方向；⑤忽略从天线发出电磁波到暗室墙面后每点变成新的余弦幅射体的再次反射；⑥忽略余弦辐射体范围以外的墙面的反射（本模型忽略了xoz墙面）.依据以上已知条件和假设，运用MATLAB软件，模拟了视在目标点的相对连续运动，如图4所示.

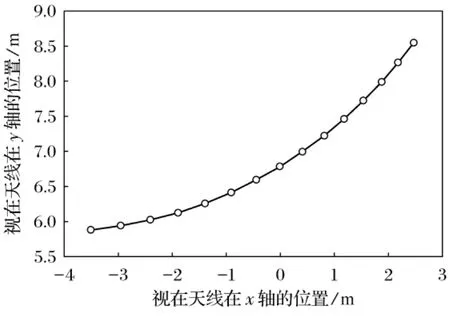
图4 视在目标P点轨迹图Fig.4 Trajectory of installed target P

若暗室铺设平板形吸波材料，其垂直反射率ρ＝0.50，此时代入上面的计算公式，运用MATLAB软件计算结果如表1所示.表明，这样的微波暗室不能满足仿真要求.在此过程中γ＞0.03，且随着视在目标越靠近静区，γ值越小.若暗室改为铺设尖劈形吸波材料时，即ρ＝0.05时，计算结果如表2所示.表明，这样的微波暗室能满足仿真要求，在此过程中γ＜0.03，且随着视在目标越靠近静区，γ值越小.