基于均匀设计的混凝土细集料级配分形试验研究

汪振双，王立久

（1.东北财经大学 投资工程管理学院，辽宁 大连 116025；2.大连理工大学 建设工程学部，辽宁 大连 116024）

分形几何学是由Mandelbrot创建的，“分形”一词的英文是Fractal，其名来自拉丁文形容词Fractal（破碎的）［1-2］.分形几何学为描述复杂问题提供了一种得力的方法，分形的核心是自相似性，分形的特征量是分形维数.目前分形几何学已广泛应用于自然科学、社会科学的各个领域［3］.分形几何学是定量描述几何形体复杂程度及空间填充能力的一门新兴学科.有许多采用传统的科学研究方法难以解决的问题，用分形理论却得到了很好的解决.混凝土宏观性能所呈现出的不确定性、不规则性、模糊性、非线性，是其微观结构复杂性的反映［4］.目前人们对混凝土微观性与宏观性的关系尚未完全研究清楚.混凝土作为具有复杂微观结构的多级多层次的复合材料体系，尤其是集料的级配具有突出的自相似性，完全可以利用分形几何学进行研究.国内学者李国强、邓学钧率先提出在集料研究中引入分形理论，并且为集料粒径、级配、比表面积等拟定了计算公式，唐明又在两人的基础上提出了更加完善一些的数学模型和更加符合实际情况的分形维数等补充结果［5］.研究表明，混凝土集料存在许多分形现象，对这些分形现象进行深入分析，是研究混凝土复杂性本质的有效途径.

1 均匀设计

实验设计的方法有单因素试验、双因素试验、随机区组试验、正交试验设计和均匀试验设计等.目前应用较为广泛的是正交试验设计法和均匀试验设计法.正交设计是古典试验设计中流行最广的一种方法，它的基点是以方差分析为统计模型，选出的代表点具有“均匀分布”与“整齐可比”的特点.“整齐可比”便于试验的数据分析，然而，为了照顾“整齐可比”，试验点就不能充分地“均匀分散”，且试验点的数目会比较多（试验次数随水平数的平方而增加）.所以当因素的水平不多、试验范围不大时，它是非常有效的试验设计方法.然而当试验需考察的因素较多且每个因素有较多水平时，运用正交设计方法所需做的试验次数仍会较多，以至于难以安排试验.20世纪70年代末，我国著名的数理统计专家方开泰与数论专家王元合作，将数论理论成功地应用于试验设计中，创立了一种全新的试验设计方法——均匀设计试验法［1］.它只需考虑试验点在试验范围内“均匀分散”，而不必考虑“整齐可比”，使试验点具有更好的代表性，因而可以大大减少试验次数，给试验者更多的选择，从而可以用更少的试验来获得期望的结果［6-7］.

2 试 验

2.1 试验材料

试验采用大连小野田水泥厂华日牌32.5水泥.细集料为天然河砂，试验用水为普通饮用水.水泥的化学成分见表1.

表1 水泥的化学成分（质量分数）Table 1 The chemical composition of cement%

2.2 试验方案设计

本试验的目的是找出不同粒径范围颗粒的分计筛余质量分数对砂浆强度和坍落度性能影响的规律，因此确定试验考核指标为强度R（MPa）和坍落度S（mm）.据此选择6个因素：X1，X2，X3，X4，X5，X6，它们分别对应的筛孔尺寸范围是4.75～9.50mm，2.36～4.75mm，1.18～2.36mm，0.60～1.18mm，0.30～0.60mm，0.15～0.30mm.根据对颗粒级配范围的规定，确定6因素的变化范围（用分计筛余来表示）如下：X1＝0～10，X2＝0～25，X3＝0～30，X4＝15～36，X5＝10～45，X6＝5～35，每个因素取9个水平［7］.试件尺寸40mm×40mm×160mm，每组做三块试件，拌合总量为1 975g.由于有6个因素、9个水平，因此选用均匀设计表U＊9（96）使用表来安排试验方案，详细配合比见表2.

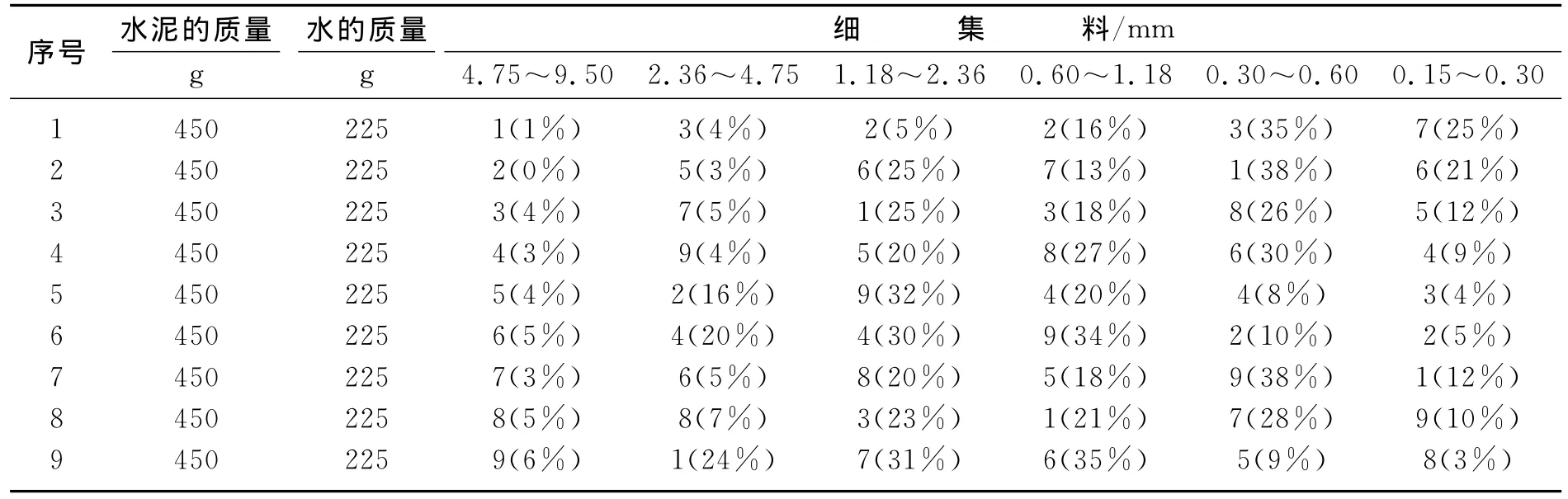
表2 试验材料的配合比Table 2 The experimental proportion

2.3 试验方法和内容

试件是在实验室制作，标准条件下养护28d后进行试验.砂浆的力学性能和扩展度均按照胶砂试验测试方法测试.抗压强度和抗折强度的试验结果取值与胶砂试验相同.

3 试验结果与分析

3.1 试验结果

试验结果见表3.

表3 试验结果Table 3 Experimental results

3.2 细集料级配分形研究

混凝土存在几种层次的分形.细骨料为砂，粗骨料一般为卵石和碎石，其表面就是一种分形.当不同尺寸的骨料混合后，代表骨料尺寸的粒径就形成一种分布，这个分布函数是一种数学分形.当不同尺寸的集料混合后，代表集料尺寸的粒径就形成一种分布，这个分布函数就是一种分形.对混凝土集料颗粒来说，设集料的颗粒粒径为φ，直径大于φ的颗粒数目为N（φ），则

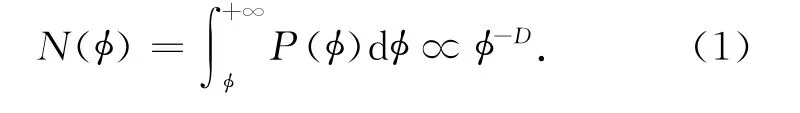
式中，D是级配集料颗粒质量分维；P（φ）为直径为φ的分布密度函数.事实上，当式（1）成立时，必然存在N（φ）∝N（λφ），λ＞0，故N（φ）和N（λφ）是成比例的［4］.

用相应的质量关系来讨论颗粒分布的分维，设m（φ）为直径小于φ的颗粒累计分形质量，mt为整形总质量，则

式中，b为lg（m（φ）／mt）与lg（φ）关系坐标的斜率.考虑到dmt∝φ3dN，则φb-1dφ∝φ3φ-（D＋1）dφ.所以集料的级配分形维数为

表3列出了不同级配细集料的分形维数，分形维数与扩展度和抗压强度的关系见图1和图2.分形维数与细集料的细度模数和最大密度曲线公式的n值的关系见图3和图4.

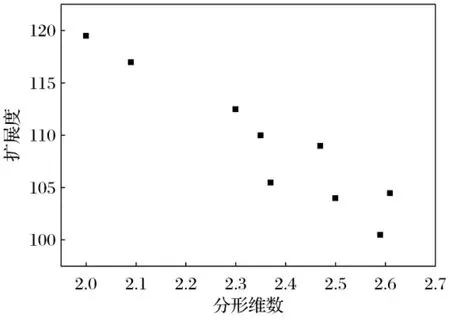
图1 分形维数与扩展度的关系Fig.1 The relationship between fractal dimension and mortar dispersion degree

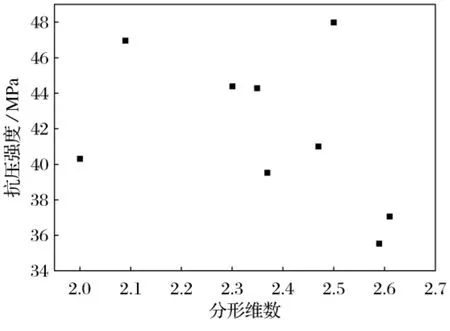
图2 分形维数与抗压强度的关系Fig.2 The relationship between fractal dimension and compressive strength

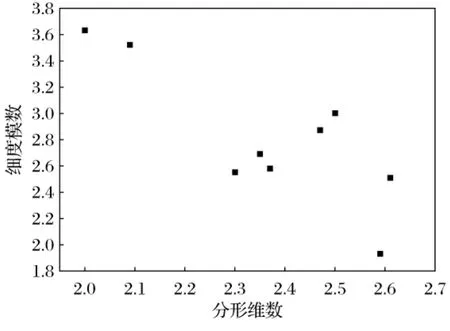
图3 分形维数与细度模数的关系Fig.3 The relationship between fractal dimension and fineness modulus

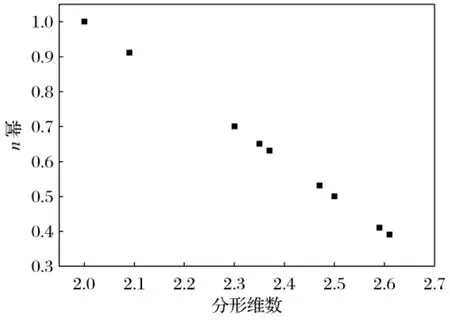
图4 分形维数与n的关系Fig.4 The relationship between fractal dimension and n

从图1和图2中可以看出，砂浆的扩展度和抗压强度随着分形维数的增大而减小，分形维数与扩展度的线性关系较分形维数与抗压强度显著.在水泥和水用量不变的情况下，细集料的级配分形维数越大，表明细集料的空间填充能力越强，集料的比表面积越大，需要包裹的水泥浆的用量也就越多.分形维数越大，砂浆的扩展度反而减小.混凝土的强度随着分形维数的增大而减小，分形维数为2和2.5时，混凝土的抗压强度出现了跳跃，且当分形维数为2.5时，抗压强度取得最大.颗粒级配在规定范围内，在水和水泥用量不变的情况下，不同的级配组成对砂浆强度的影响比较显著.抗压强度结果与富勒曲线结果吻合.而细度模数和n值随着分形维数的增大而减小.混凝土用砂的原则是，在满足级配要求的范围内，尽量选用粒径较大的砂子.细度模数越小，细集料的粒径越小，比表面积越大，分形维数越大.细集料质量函数的分形模型与最大密度曲线理论提出的公式具有相同的表达形式，即公式中的n等于简化公式中的3-D，根据试验认为n＝0.3～0.6时，具有较好的密实度，从而验证了上述推导的正确性.

4 结 语

（1）利用均匀设计方法对混凝土细集料级配进行了研究，在扩展度相差不大的情况下，第5组试验结果的强度最高，从而确立了较优的颗粒组成.即细集料粒径区间（mm）分别为4.75～9.50，2.36～4.75，1.18～2.36，0.60～1.18，0.30～0.60，0.15～0.30.其对应区间的分计筛余质量分数（%）分别为4，16，32，20，8，4.

（2）混凝土是一种微观结构和力学性能都很复杂的工程材料.将分形理论引入混凝土领域中，用分形维数D对试验结果进行了描述和分析.细集料级配的分形维数越大，骨料自密实填充性能越好，则混凝土强度越高.集料质量函数的分形模型与最大密度曲线理论提出的公式具有相同的表达形式，从而可从微观层面上解释级配的分布特征.

（3）混凝土细集料分形维数是一个描述复杂问题的定量参数，它包含了细集料在空间上的填充能力，还涵盖了细集料级配的组成变化，因此细集料分形维数可定量描述细集料性能，能够起到连接细集料性能与混凝土性能的桥梁作用，可以成为指导混凝土设计的定量指标.

［1］ 肯尼思·法尔科内.分形几何中的技巧［M］.曾文曲，王向阳，陆夷，译.沈阳：东北大学出版社，1999.

［2］ Mandelbrot B B.Fractal character of fracture of metals［J］.Nature，1984，308（19）：721-722.

［3］ 张国祺，李后强.分形理论对世界认识的意义［J］.大自然探索，1994，13（1）：11-16.

［4］ 夏春，刘浩吾.混凝土细骨料级配的分形特征研究［J］.西南交通大学学报，2002，37（2）：186-189.

［5］ 姜晓伟，宓永宁，高跃.不同分维骨料级配对混凝土性能的影响研究［J］.房材与应用，2006（2）：5-7.

［6］ 周梅，汪振双，李塑忠.基于均匀设计的逐步回归法预测树脂混凝土强度研究［J］.硅酸盐通报，2007，26（5）：924-928.

［7］ 吴浩，管学茂，李荣军.均匀设计在煤矸石填充材料颗粒级配试验中的应用［J］.水泥工程，2006（6）：13-16.