海杂波中的超视距雷达探测性能分析
2012-10-27康士峰王红光
孙 方, 康士峰, 王红光
(中国电波传播研究所,山东 青岛 266107)
0 引言
大气波导是当大气修正折射率梯度小于零时的一种反常大气层结[1]。海洋大气环境中由于温度的逆增和湿度随高度的剧烈递减,经常会出现表面波导和蒸发波导,它们可以捕获微波频段低仰角传播的电磁波,使得波导高度内工作的微波雷达系统探测到正常大气环境下原本探测不到的远超视距的目标。然而,雷达在实现超视距探测的同时,大气波导同样会将正常探测条件下不可能出现在雷达显示屏上的远处的海杂波显示在雷达显示屏上,从而大大增加了雷达杂波信号强度,使目标淹没在海杂波中,降低了雷达的检测分辨性能。针对这一现象,利用雷达性能评估模式,仿真计算了雷达在不同发射频率、发射仰角以及架设高度下,蒸发波导和表面波导两种环境中海杂波和目标的回波功率,进行了海杂波干扰下微波超视距雷达的探测性能分析与评估,可对雷达设计、辅助战术指挥员进行正确战术部署和选择恰当的作战战术,提供参考。
1 海杂波与海上大气波导模型
1.1 海杂波模型
海杂波的强弱通常用海面散射系数0σ表示,即单位面积的雷达后向散射截面[2]。为了方便统计和研究海杂波,建立了一些0σ与各种参数(掠射角、风速和频率)的海杂波模型。海杂波的常量γ反射率模型为:

式中,ψ为海面的掠射角,不同的发射仰角对应在不同距离上的掠射角不同,在波导环境中通常利用射线追踪技术进行计算[3],图 1给出了典型波导环境下掠射角随距离的变化。
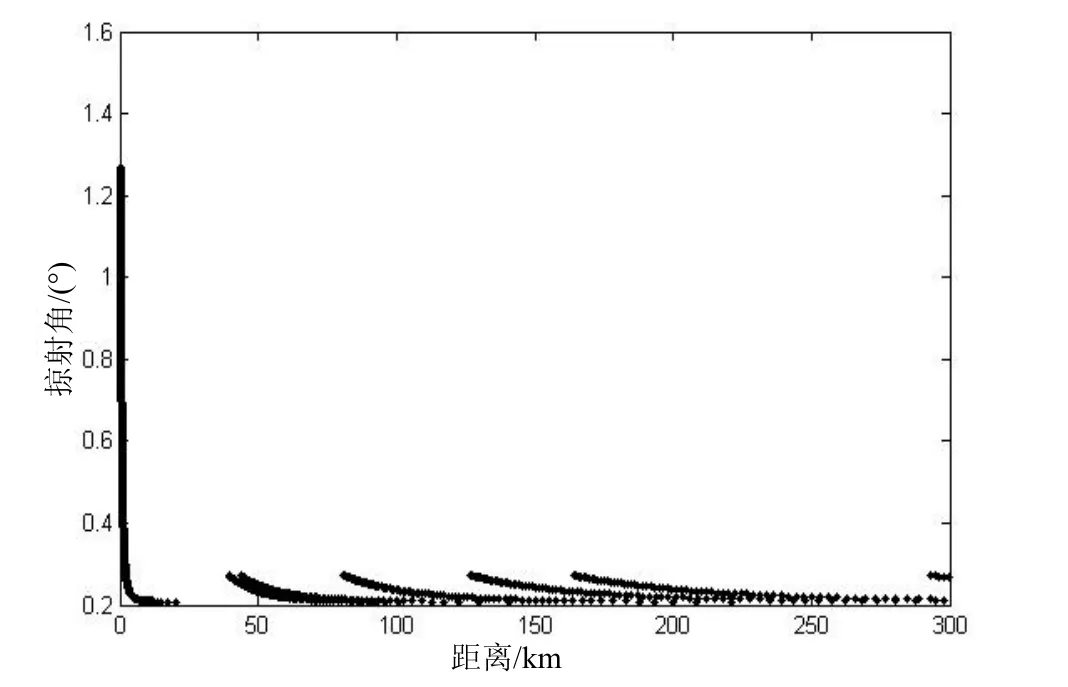
图1 波导环境下掠射角随距离的变化
γ为描述反射率的参数:
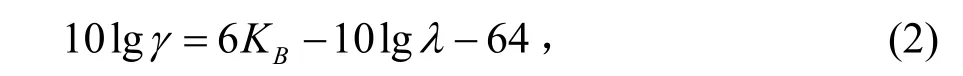
式中,λ为波长,KB为Beaufort风级数,于是可以得到:
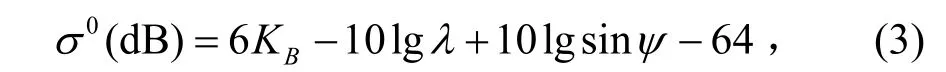
然而,由式(3)得出的反射率数据与实验数据有很大的误差。Song[2]对这个模式进行了改进:
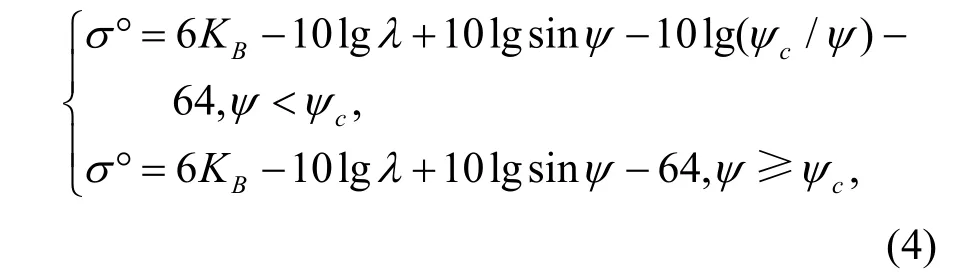
这里,ψc为临界掠射角,它与海况有关:

式中,he为海面粗糙度:
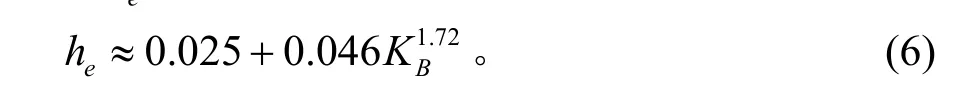
1.2 海上大气波导模型
大气波导模型通常用修正折射率随高度的变化表示。蒸发波导和表面波导是海上出现频率较高的两种大气波导,尤其是蒸发波导,其出现概率高达 80%以上,在低纬度海域往往是永久性的[4]。表面波导在海上出现的概率平均不到40%,虽然远低于蒸发波导,但其波导高度一般较高,范围从几十米到几百米都有可能,且表面波导模型为线形模式,因此其陷获电磁波的能力一般远高于蒸发波导。这里引入Peter Gerstoft提出的一个由5个参数组成的比较完善的模型[5],模型图示为图2所示。
这个模型描述了包括了蒸发波导和表面波导在内的波导类型,其具体表达式为:


图2 五参数大气折射率模型
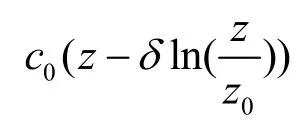
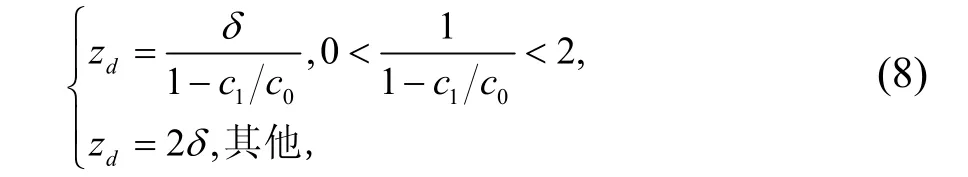
zb是波导层结的底高,zthick是逆增层的厚度,zt定义为:

M0=330M,是修正折射率剖面的初始值,定为混合层斜率和z=0相截的值,M1的表达式为:
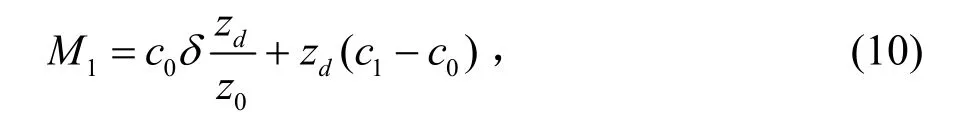
Md是逆增层的修正折射率变化量。
2 雷达性能评估模式
对于收发共置的雷达系统,雷达距离方程为:

式中,Pt为发射机发射功率, Pr为接收机接收功率,G为天线增益,R为目标至雷达的距离,Ls为系统损耗,La为大气吸收损耗,λ为雷达波长,σ为目标的雷达截面积,F为传播因子。将传播因子用传播损耗L表示,并以dB为单位,可以写成:
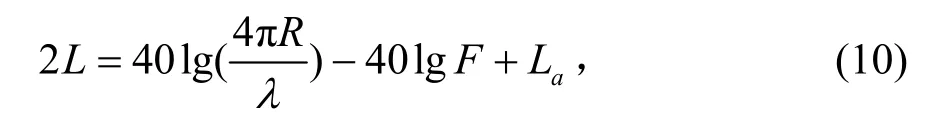
电磁波在大气波导中的传播损耗通常利用分步傅立叶解法的抛物方程模型进行计算[6]。则目标的回波功率以dB为单位,可以写成:
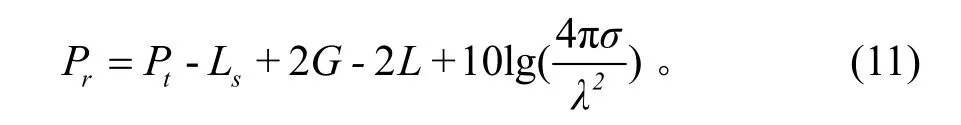
对于海杂波,其反射面为海面,可以使用关系式σ=Acσ0来表示海面的雷达散射截面,其中Ac是被照射面积,如图3所示。
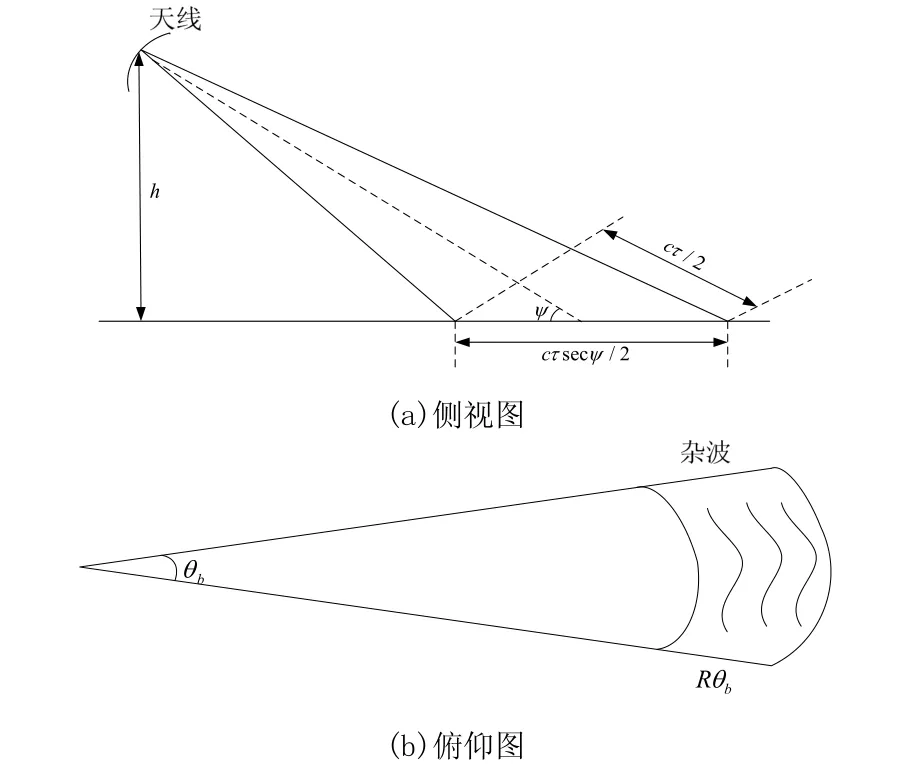
图3 雷达站和杂波的关系示意图
在小掠射角时Ac是距离的线性函数,

式中,θkbw为雷达水平波瓣宽度(rad),脉冲宽度为τ( s),照射表面的掠射角为ψ,则海杂波的回波功率以dB为单位可以写成[3]:
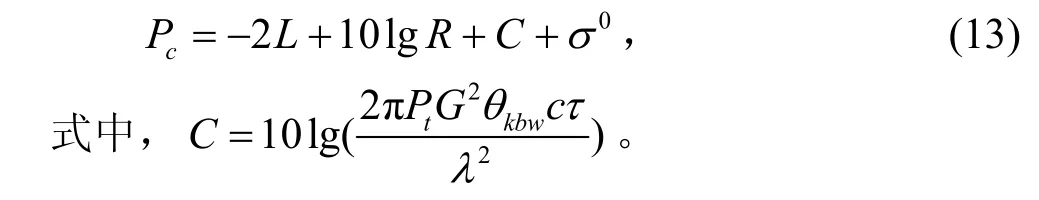
雷达的最小可检测信号功率为:

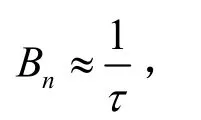
只要目标的回波功率Pr≥Smin,雷达即可检测到目标,反之,即便存在目标雷达也无法检测到。同样,当海杂波功率Pc≥Smin时,雷达很可能将海杂波误认为目标。在海杂波抑制方面,雷达系统内部会对杂波进行信号处理[7-10],此外,还可以通过减小波束宽度,减少雷达对海面的照射面积来降低海杂波信号强度,但减小波束宽度就要增大天线直径,在造价和环境上受到多方面的制约。这些方法在一定程度上改善了海杂波的干扰,但并不能保证与真正的目标完全区分。为了更大程度的减小海杂波的干扰,针对大气波导这一特殊环境,通过改变雷达的发射频率、发射仰角以及架设高度,寻找最佳的系统组合,减小杂波信号的幅度,使 Pc<Smin,且Pr≥Smin的出现概率最大化。在实际作战环境中,如果雷达的这些系统参数允许调节,那么根据大气环境条件选择合适的系统参数,就可以大大减小海杂波信号幅度,进一步提高雷达的探测性能。
3 仿真结果分析
这里选取的大气波导剖面如图4所示,低层为蒸发波导,高层为表面波导。
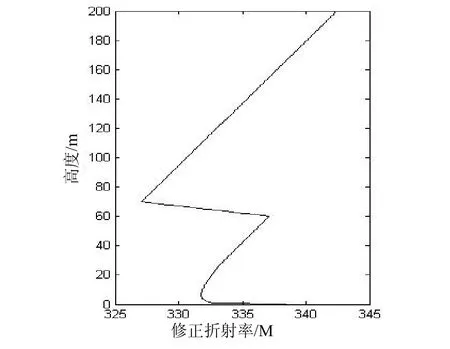
图4 大气波导剖面
海态等级设为 3,即中浪时的海况,令浪高为1 m。目标设为截面积为10000 m2的海上舰船,则海杂波的传播损耗即为高度1 m时随距离的变化,目标的传播损耗为高度10 m时随距离的变化。设雷达水平波束宽度为1.5°,发射功率150 kW,天线增益40 dB,脉冲宽度20 μs,系统损耗3.5 dB,接收机噪声系数3 dB,检测因子14.7 dB,则由式(14)计算得到的最小可检测功率为-139.3 dB,由式(13)、式(11)计算海杂波与目标随距离变化的回波功率。为了更加直观的分析海杂波干扰下的雷达探测性能,这里统计探测距离在0~1000 km范围内:Pc≥Smin时的出现概率 P1; Pr≥Smin,且Pc<Smin时的出现概率P2;以及Pr<Smin时的出现概率 P3。显然, P2越大,雷达探测性能越好。
令雷达架设高度为10 m,发射仰角为0°,图5给出了上述3种情况的出现概率随频率的变化。
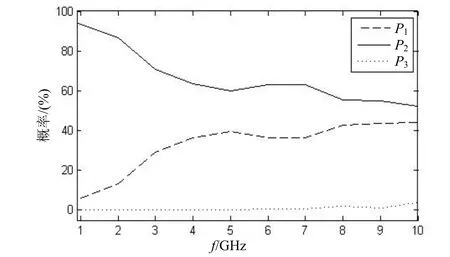
图5 3种情况概率随频率的变化
令雷达架设高度为10 m,发射频率为3 GHz,图6给出了3种情况的出现概率随发射仰角的变化。
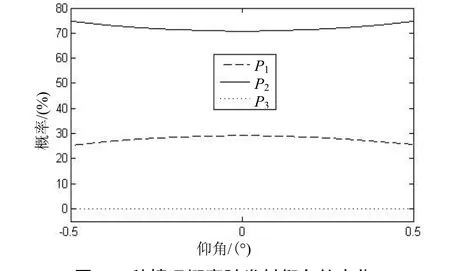
图6 3种情况概率随发射仰角的变化
令发射仰角为0°,发射频率为3 GHz,图7给出了3种情况的出现概率随天线高度的变化。

图7 3种情况概率随天线高度的变化
根据上述计算结果,该大气波导剖面中,雷达系统在天线高度 8 m,发射仰角-0.5°,发射频率0.9 GHz时探测性能最佳,在天线高度62 m,发射仰角0°,发射频率10 GHz时探测性能最差,图8、图9给出了最佳与最差时目标与海杂波回波功率随距离的变化。
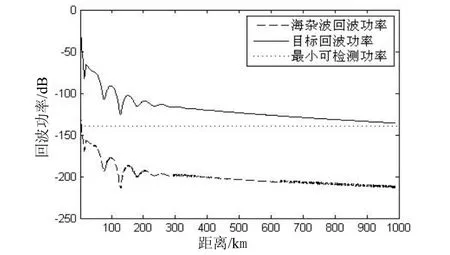
图8 8GHz下目标与海杂波回波功率随距离的变化
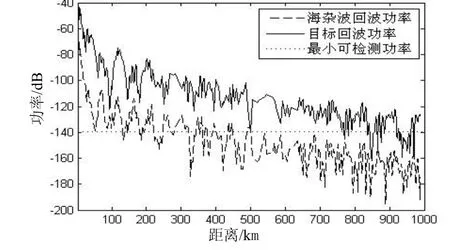
图9 10GHz下目标与海杂波回波功率随距离的变化
雷达在最佳探测性能时P1=3.9,P2=96.1,P3=0;雷达在最差探测性能时P1=52,P2=38.4,P3=9.7。由此可见,雷达系统参数的设置对其探测性能影响很大,在实际操作中,如果雷达频率、架设高度或发射仰角可调,那么选择合适的参数将大大降低海杂波的干扰。
4 结语
分析了海杂波干扰下微波超视距雷达的探测性能。针对海上常见的大气波导类型,当雷达系统的基本参数一定时,通过改变发射频率、发射仰角与架设高度,可以有效的降低海杂波对雷达系统的干扰,同时又不容易遗漏较远距离处的目标,大大提高雷达的探测性能。这里仿真的典型波导下海杂波与目标回波信号的结果不一定适合所有类型的波导,但却具有一定的代表性,后续工作将针对更多不同高度、不同强度的波导类型进行计算,如能总结出规律性的结论,可以根据海上环境建立一种自适应雷达系统,对于海上作战指挥与决策会有进一步的指导作用。
[1]熊皓.电磁波传播与空间环境[M].北京:电子工业出版社,2004.
[2]韩杰.基于海杂波反演近海面大气折射率剖面的研究[D].青岛:中国电波传播研究所,2008.
[3]孙方,赵振维,王红光,等.海上湍流效应对大气波导传播的影响[J].现代雷达,2011,33(02):13-17.
[4]刘成国,黄际英,江长荫,等.用伪折射率和相似理论计算海上蒸发波导剖面[J].电子学报,2001,29(07):970-972.
[5]王波.基于雷达杂波和 GNSS的大气波导反演方法与实验[D].西安:西安电子科技大学,2011.
[6]王红光,张蕊,康士峰,等.大气波导传播的抛物方程模型研究综述[J].装备环境工程,2008,5(01):11-15.
[7]牟泽磊,沈晓峰,雷钟凯.动目标检测与速度估计仿真研究[J].通信技术,2010,43(11):55-58.
[8]赵寅,周新志.雷达信号处理中动目标检测的研究[J].通信技术,2011,44(03):139-140.
[9]郑晓丽,姜迪刚.跳频同步信号的最佳干扰[J].信息安全与通信保密,2007(01):85-86.
[10]高智芳,张新家.基于小波变换的除噪方法及其应用研究[J].信息安全与通信保密,2007(06):102-104.
