陕北榆林地区混凝土箱梁温度梯度分析

2012-10-26高大峰何新成任禹州

太原理工大学学报 2012年2期

高大峰，何新成，任禹州

（西安建筑科技大学结构工程与抗震教育部重点实验室，西安 710055)

自20世纪50年代以来，国内外学者通过对桥墩裂缝的现场调查分析，认识到温度应力对混凝土桥梁结构安全的重要性。由于自然环境中的混凝土箱梁不可避免地会受到诸如阳光辐射、气温变化、风速等因素的影响，加之混凝土的热传导性能差，使得结构内部产生较大非均匀温度场，并由此产生相应的温度变形，当这种变形受到约束时，会引起较大的内力。根据现场车载实验数据与混凝土结构应变实测数据的对比发现，温度应力与20t的装载机通过桥梁时所引起的箱梁应力相当。有的预应力混凝土桥梁因而发生严重裂损。上世纪60年代起，国内外桥梁工作者基于Fourier热传导理论和现场实测数据分析得出某一地区温度梯度模式［1］。然而，混凝土结构温度场的确定与太阳辐射强度、桥梁方位、日照时间、地理位置、地形地貌等因素有关，为考虑温度对桥梁结构内力的影响，各国桥梁规范给出了沿箱梁截面高度的温度梯度模式［1］。我国现行的公路桥梁设计规范采用了美国规范的温度梯度模式，并做了适当的修改，相关文献［2］分析表明将单一的温度梯度分析模式用于不同地区不同桥型箱梁的设计是不合理的，即由于混凝土箱梁的布置特点和地区自然环境的差别，不能简单地套用某个地区的温度梯度模式，而须通过具体的实例来分析该地区的混凝土箱梁的温度场分布状况，对该地区同类桥梁温度计算给出参考温度梯度模式。现以陕西府谷县华建大桥的施工监控数据为基础，基于传热学理论，计算该结构箱梁截面理论温度场，通过与实测温度场数据的分析比较，以此研究在冬季太阳辐射作用下其整个截面温度场的分布状况，确定适合该地区冬季混凝土箱梁沿截面高度分布的温度梯度表达式。

1 混凝土箱梁截面温度测点布置与观测

华建大桥为独塔无背索斜拉桥，东西走向，跨径布置为（40＋60＋42)m，全长143.58m，桥面宽20 m。其结构布置如图1所示。为反映在日照作用下沿桥纵向不同位置箱梁截面温度场的分布状态，选取4个温度观测截面。测试时段从2010年11月27日零时到11月29日零时，期间每2h测一次。测试内容包括大气温度、风速、以及各截面沿梁高度分布测点的温度。

图1 关键部位温度传感器布置图

图2 桥址环境温度

本文对11月28日观测的温度数据进行分析，其白天桥面上风速平均为1m／s，晴，无云。桥址环境温度变化如图2所示，实测气温变化范围为-9～8℃，因太阳辐射作用，桥面温度幅度变化较大，最高温度出现在14：00；由于箱梁室内空气处于封闭状态，温度幅度变化不大，最高温度出现在18：00，相对于桥面出现最高温度的时刻滞后了4h；箱梁底部气温变化趋势与大气温度变化相似。对沿桥梁纵向各截面实测数据进行分析表明，自截面1向截面4桥址环境温度依次递减，截面1和截面4的最大温差出现在14：00，温差值为1℃。

2 混凝土箱梁温度场数值分析

2.1 理论基础

实际工程中混凝土箱梁温度场处于非稳定状态，其热量传递随时间而变化。而热量传递的基本方式有导热、对流和辐射三种。

1)导热。即物体各部分不发生相对位移，依靠分子和原子及自由电子等微观粒子的热运动而产生的热量传递形式。现假设混凝土材料为匀质、各向同性，则某点i瞬态温度为

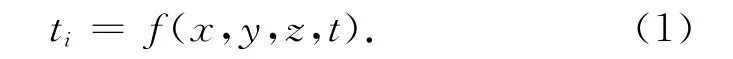
由于实测桥面纵向的温差最大值仅为1℃，并结合以往相关研究［3］，可以忽略桥梁纵向的热流效应，本文研究的是浇筑混凝土28d后的温度场分布，其时混凝土的水化热效应已基本完成，根据Fourier热传导理论，混凝土箱梁的热传导规律可近似地用二维非稳定导热方程表示

式中，λ为混凝土的导热系数；c为混凝土的比热；γ为混凝土的容重。

2)热对流。即箱梁表面与其所接触流体间因存在温差而引起的热交换。由于箱梁与周围空气发生对流方式的热传递，其对流换热计算的理论依据为 Newton冷却定律［4］。

3)太阳辐射。即太阳向周围空间发射的电磁波能量及粒子流。辐射强度与混凝土对其吸收率将直接影响箱梁温度场的分布［5-6］。因其影响较大，且太阳辐射对混凝土温度场的影响比较复杂，依相关文献［7-8］可知，榆林地区12月份月辐射总量为80 kW·h／m2，可以计算出日平均辐射量，由文献［9］中所指出的日照辐射强度随时间变化的函数，并按照我国现行《民用建筑热工设计规范》［10］所建议的公式，换算出室外太阳每小时辐射的折算温度

式中：α为辐射吸收率，取为0.60；I为太阳辐射强度，W／m2，αC为混凝土外表面换热系数，W／（m2·°C)。

2.2 单值性条件

在求解导热微分方程时，需要确定相应的箱梁单值性条件：几何尺寸，物理条件，初始温度场条件以及箱梁边界条件。

1)因桥梁为东西走向，箱梁两室对称，且腹板不受日照，故取箱梁一侧建模分析。

2)混凝土热物理性质主要指标包括导热系数k和比热容c，其与混凝土骨料的种类、用量及混凝土含水状态等因素有关［6］。该桥混凝土强度等级为C50，骨料为砂岩，取导热系数为3J／（m·s·℃)，比热容取为880J／（kg·℃)。在风速小于5m／s时箱梁对流表面热换系数按文献［6］中的相关公式确定，则箱梁顶板上表面、边腹板外表面、底板外表面以及箱梁室内表面对流换热系数分别取为8.5，7.5，6.0，3.5W／（m2·℃)。

3)设初始温度场条件为11月28日6：00的桥址温度，施加到模型边界上，用Ansys进行稳态分析，得到相应的初始温度场。

4)箱梁顶板由于受到太阳辐射的影响，将11月28日6：00—17：00时段的太阳辐射值按式（3)折算成温度值与桥面遮阴处的气温，作为顶板的边界条件。根据实测和计算数据，并采用以往研究成果中有关的数学模型［11］进行拟合，得出箱梁顶板、边腹板、底板及室内空气温度随时间变化的边界条件：

式中，t为时间，h.

2.3 有限元模型分析

基于Ansys软件平台建模，采用二维四节点PLANE55单元，单元划分最大尺寸为0.05m。

其有限元模型如图3所示。

图3 箱梁有限元模型

分析时段设为11月27日零点到11月28日零点，分成24个荷载步，每个荷载步又分成100个子荷载步，并施加边界条件分别进行稳态和瞬态分析。图4上下分别是8：00和15：00时的温度分布云图。

图4 箱梁断面温度分布图

从图4中可以看出，在8：00时，箱梁悬挑板中的温度最低，接近于室外大气温度，是因悬挑板较薄且完全暴露在大气中的缘故；而室内温度则相对较高，此时中腹板温度达到最高。顶板和底板的温度则相对均匀。15：00时箱梁顶板温度最高，且其横向及纵向的温差较小，顶板和底板的温差则变化较大。箱梁截面在进行热传导的过程中，混凝土表面与外界空气同时进行着对流换热，遂导致纯粹通过热传导所传递的热量减少，由于混凝土导热性能较差，致使混凝土箱梁截面沿高度方向存在较大温差。而在腹板与顶板、底板的交界处，相对于其他部位温度最低，最大温差达11.2℃，是由于箱梁梗腋高度对温度梯度的影响［6］以及混凝土导热性能较差所致。随着热传导的持续，这种温差遂逐渐减小。

2.4 混凝土箱梁温度梯度的拟合

由于沿桥纵向的温差较小，而当15：00时箱梁截面温差较大，故选取1-1截面15：00时顶板和底板上单元节点的温度来分析以确定箱梁截面的最大温度场分布。箱梁截面沿其高度的温度分布如图5所示。

可以看出，边腹板较中腹板的温差大，故选取边腹板进行沿腹板高度方向温度梯度的拟合。混凝土箱梁顶板沿高度方向的温度变化较快，在0.3m范围内温差即达到11.2℃；而箱梁腹板的温度随高度的变化很小。由于箱梁梗腋高度较大以及混凝土的导热性能较差，遂使得腹板与顶板、底板相交处存在低温区；在底板没有布置测点，根据计算值可知，随着靠近箱梁底板，温度值则逐渐变大，接近于直线变化。腹板与底板的最大温差为5℃。计算表明，冬季箱梁顶板和底板的温差较大。