战场电磁环境构建中的抛物方程应用研究
2012-10-25来嘉哲方广有
来嘉哲 方广有 刘 帅
①(中国科学院电子学研究所 北京 100190)
②(中国科学院研究生院 北京 100049)
③(解放军装备学院 北京 101416)
1 引言
在信息化战争中,复杂的战场电磁环境已经成为影响各类电子装备作战效能发挥的主要要素,战场电磁环境的相关问题研究已成为战争仿真的热点。研究战场电磁环境的构建方法,模拟出符合实际战场中复杂的电磁环境态势,对于推动电子装备的快速发展和作战仿真的应用具有重要的意义。
战场电磁环境的构建可以采用物理或数学的方法,按照预先设置的场景生成电子战系统所面临的战场电磁环境,模拟战场上的电子战行为。战场电磁环境的构建按具体的实现方式分为以下4种:外场模拟、微波暗室仿真、注入式仿真和全数字仿真。前3种方式属于实物半实物仿真的范畴,利用实际的电子设备形成射频信号来模拟战场电磁信号,逼真性好,可用于电子装备的试验,但是受试验环境的影响和制约,难于体现出实际战场电磁环境要素的影响。而全数字仿真方法可以任意设置辐射源和环境要素,手段灵活,利用计算机可快速构建任意设置的战场电磁环境,便于系统的分析和设计。
战场电磁环境的数字化构建中,最主要的是能够计算出各类辐射源在实际传播要素影响下的传播过程,在可实用的电波传播模型中,能够快速准确地预测不规则地形与复杂大气条件下电波传播特性的方法是抛物方程(Parabolic Equation,PE)[1]。与时域有限差分法、射线跟踪法等方法相比,抛物方程方法计算效率更高更精确,特别适合计算远距离电波场,得到了人们广泛关注。
国外较早开展了基于PE模型的电磁环境研究,如美国空间和海军作战系统中心开发的 AREPS[2](Advanced Refractive Effects Prediction System),主要是基于抛物方程方法,可预测复杂环境下电波传播特性。由于最常用于求解 PE模型的算法是一种步长迭进的方法,难于实现算法并行化,对于战场电磁环境的数字化快速构建造成了困难。
本文提出了一种基于并行计算机架构的数字化战场电磁环境构建方法,在输入各个辐射源参数、地形数据和大气参数的情况下,利用抛物方程模型计算电波传播的过程,得出整个区域的场分布,从而模拟出复杂的战场电磁环境。在计算的过程中,设计了并行算法来充分利用计算集群的运算能力,加速模型的实际求解过程。计算机仿真结果验证了该方法具有较好的性能,能满足大区域战场电磁环境的构建需求。文中第2节对抛物方程模型的基本原理和数值算法进行了介绍,通过与双射线模型的比较,验证了该模型的正确性;第3节给出了并行算法的基本设计思路和实现流程;第4节给出了系统的运行流程和仿真计算结果,证明了并行算法的有效性;第5节给出了结论。
2 抛物方程模型
研究在直角坐标系(x,y,z)中电波的传播问题,假设电波只是在2维平面中(x,z)传播,x为传播方向,电磁场的时谐因子为e−iωt,i为复数单位,ω为角频率,场量ψ在传播过程中满足以下2维标量方程[3]

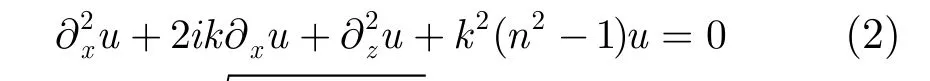

式(3)中的两个因式相互独立,分别代表了电波的前向和后向传播过程,在只考虑前向传播的情况下,式(4)已能很好的描述电波的传播过程:
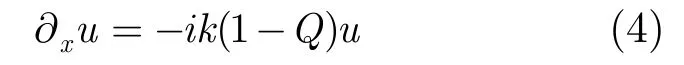
伪微分算子Q中包含了根式和二阶微分形式,在进行求解时无法得出简单的解析表达式,因此需要对算子作相应的近似处理。最常用的方法是采用Taylor近似法,利用Taylor展开的一阶近似表达式:

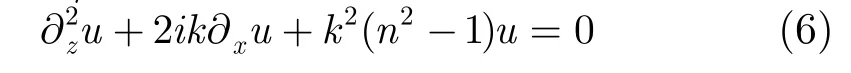
式(6)即为标准抛物方程(Standard Parabolic Equation,SPE),与式(2)所表示的椭圆方程相比,两式的主要差别在于标准抛物方程忽略了高阶偏微分项,即基于这一事实,忽略了项。SPE的误差项主要是Taylor展开中忽略的二阶无穷小量O(z2)。以传播仰角为α的平面波为例,其谐函数表达式通常为u(x,z)=exp[ikx(cosθ−1)+ikzs inθ)],可得出。因此忽略的二次项,即整个方程的误差正比于 s in4α。在传播仰角为10°时误差项正比于10−3,35°时误差项正比于 1 0−1,可见SPE适合于传播仰角较小的场合,以目前的非接触作战模式为例,辐射源和目标的距离都在上百公里,能够满足SPE的传播仰角需求。
SPE常用的求解方法是分步傅里叶法(Split-Step Fourier Transform,SSFT)[4]。SSFT是一种步进迭代的算法,其基本思路是在当前计算点将高度域变换成频率域,利用频率域的快速算法完成计算后变换回高度域,再向前逐步推进,从而计算出整个区域的场分布。该算法求解速度快,稳定性好,本文采用该方法完成战场电磁环境的构建。
SSFT算法定义傅里叶变换对如下:


对该微分方程求解,可以得出

上式的两个指数项分别代表了折射项和绕射项,作傅里叶逆变换后可得出

SSFT算法的步进过程如图1所示。
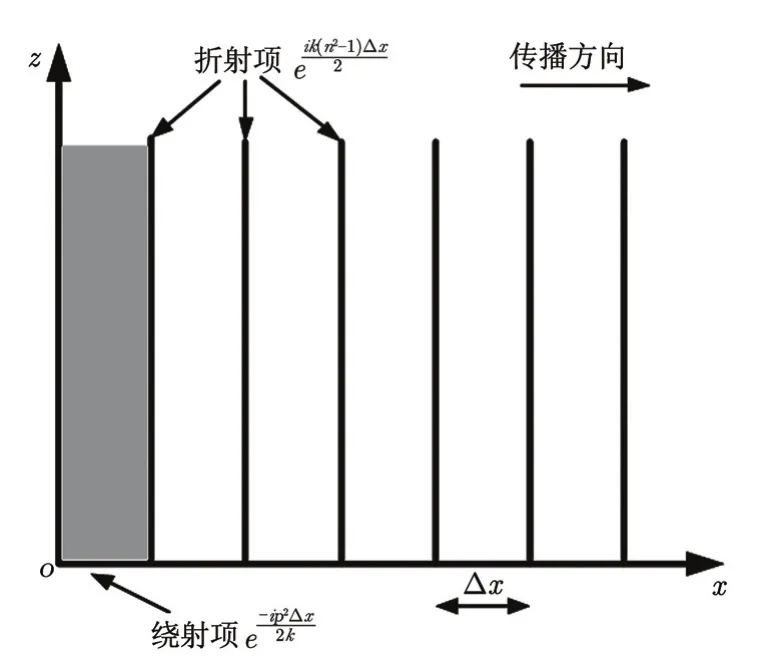
图1 SSFT算法示意图
实际的战场上受电磁环境影响最大的装备类型是雷达和通信装备,所以战场电磁环境数字化构建过程中考虑的频率范围是30 MHz~12.5 GHz。大气环境对电波传播的影响主要体现在式(10)中折射指数n的变化上,实际环境中n的值会随高度和传播距离发生变换,通常可以利用通用的折射率模型计算得出,也可依据实际测量值输入。战场环境的地理覆盖范围较大,其地理数据可通过 DEM 数字地图文件来获取,并利用数据内插的方法构建出电波传播的地形剖面。实际的地表起伏不定,可以采用移位变换地形模型来处理地表起伏[5],并结合阻抗边界条件,采用离散混合傅里叶变换算法(Discrete Mixed Fourier Transform,DMFT)来解决边界条件[6]。
PE方程的推导和 SSFT算法中都采取了一定的近似方法,但其电波传播预测的影响程度很小。下文以双射线模型作为基准参考模型,验证其正确性。双射线模型的传播因子理论值为

式中 ΔR为直达波与反射波的程差,k为自由空间波数,Γ为地面的归一化反射系数,取辐射源天线高度20 m,电磁波频率为2 GHz,地面介质导电率σ=30 mS/m,εr=5,接收点距发射天线距离为10,000 m,利用SSFT算法的计算结果和双射线模型的理论值对比如图2所示。
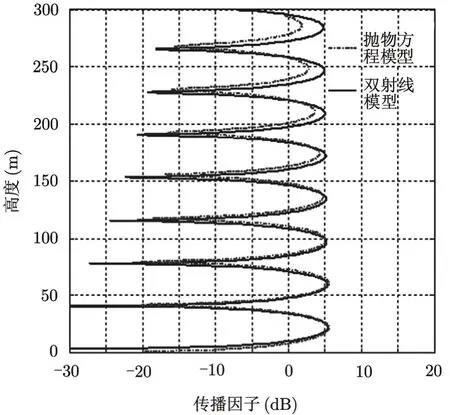
图2 抛物方程与双射线模型结果比较
接收点的高度范围是从地表至300 m,图2显示了2种方法计算值的符合程度较高,说明抛物方程模型和SSFT的精度能够满足战场电磁环境的构建需求,所需要解决的问题就是在频率高、传播距离远的情况下如何快速完成传播过程的计算工作。在单台工作站计算能力有限的情况下,可以利用高性能计算集群,构建适合并行计算的传播算法,提高算法中最为耗时的离散傅里叶变换(DFT)的计算速度,加速SSFT的求解过程。
3 并行算法设计
为解决SSFT求解过程中 DFT运算的耗时问题,本文采用了矩阵转置的并行算法,该算法的基本思想是:将1维序列分解成较小规模的子数组,构成 2维矩阵,继而对 2维矩阵行、列分别计算DFT[7]。由于矩阵的各行之间、各列之间DFT计算是独立的,便可以将2维矩阵按行或列分发给不同的进程,实现数据并行计算。该算法可扩展性强,将通信集中于一步内完成。
设N=N1×N2,记

并行计算DFT有如下5步:
(1)每个进程负责矩阵u(n1,n2)的N1P行,并对每行做N2点DFT;
(2)对结果的每个元素乘以相应的旋转因子En1n2=exp(−(2πj/N)n1n2);
(3)将所得中间结果矩阵进行转置,使其按列重新分配;
(4)每个进程负责矩阵的N2P列,并对每列做N1点DFT;
(5)最后再次进行转置操作,使矩阵元素在各进程的分布回到原矩阵的顺序。
在求解抛物方程的SSFT算法中,需要大量的DFT计算,本文基于矩阵转置的并行计算其核心是:先不做DFT并行算法的第(5)步,而是将绕射项指数转置,直接与第(4)步所得结果相乘,这样避免了第(5)步转置操作所带来的全局通信开销,这样处理提高了并行计算效率。完成绕射项指数计算后,按照(1)~(4)步相反的顺序做IDFT变换,只是其中使用了旋转因子的共轭项,最后计算折射项[8]。
仿真实现中并行算法流程如图3所示。
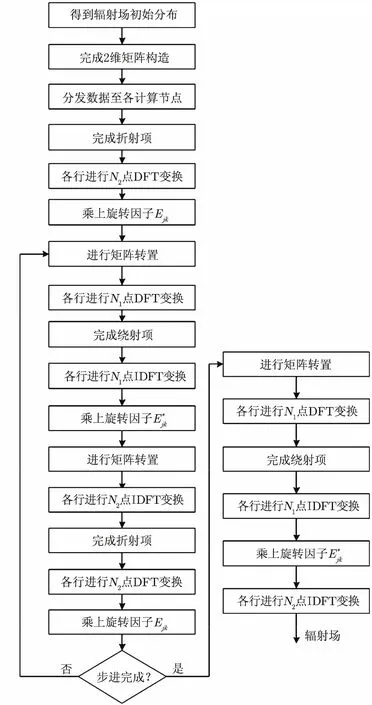
图3 矩阵转置SSFT算法并行方案流程图
本方案中计算并行性主要体现在如下3方面:
(1)由于折射项、绕射项的计算不依赖于输入序列,可以在迭代开始前将其计算出来存储到各节点的本地存储器上;
(2)各个进程分别计算出所有的旋转因子,但计算时只取用该进程所对应的部分,这样做同时简化了程序实现难度;
(3)行、列变换在各进程内独立进行。
4 系统仿真结果
系统采用的集群系统是银河高性能计算集群,计算单元包含8组×10片刀片式计算机,系统峰值性能为11.2512 TFlops。系统实现过程中使用MPI作为并行计算的消息传递接口,它对并行算法的表达能力强,性能高,可移植性好,已经成为并行编程事实上的标准。系统的运行流程如图4所示。

图4 系统运行流程图
在完成大气环境、地形和辐射源等参数的输入之后,系统进行MPI的初始化,将任务分解到各个运算进程中去,各个进程完成初步运算,并利用MPI的通信机制进行数据交换,完成并行算法中的矩阵转置,并逐步向前推进,完成整个区域的战场电磁环境构建。
以高度域上的离散点数为 212个点,推进步数4000步为例,采用基于矩阵转置的SSFT整体优化并行算法对SSFT算法进行求解,其中矩阵的行数和列数均取64。在并行机上的测试结果如表1所示。

表1 并行算法的加速比和效率(212点)
若取高度域上离散点数为214点,其余的条件不变,在并行机上的测试结果如表2所示。

表2 并行算法的加速比和效率(214点)
图 5为在不同的输入条件下系统的加速比曲线,相比于单机上实现的串行算法,利用并行机和并行算法,速度可以提升到4倍以上。同时仍然可以看出并行算法的加速比相对于理想的线性加速比还是存在着一定的差距,主要的原因在于:在使用矩阵转置的并行方法时,每一步迭代过程都需要进行2次矩阵行和列的转置,用于矩阵中各个元素的DFT和IDFT实现,导致了算法的通信开销。但是相比于单纯的使用FFTW的MPI版本等现成软件的粗粒度并行方法,其通信开销已经减少了近一半。
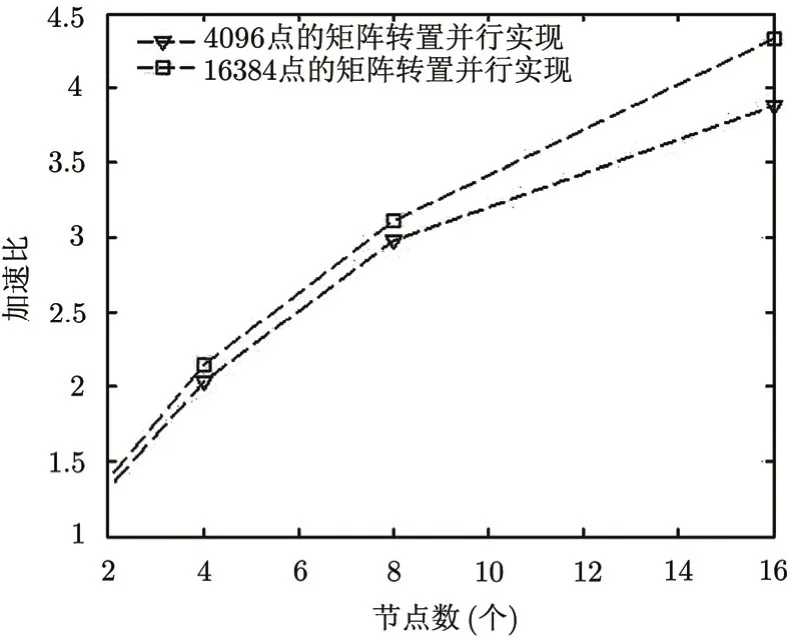
图5 加速比曲线
从图5还可看出,随着高度域离散点数的增加,系统加速比有所增加,这说明并行算法中计算耗费的时间相对于通信时间的比例在增加。综上所述,随着用于战场电磁环境构建任务的计算节点的增加,运算速度在不断的增加,而且随着采样点数的增加,计算强度越来越大,系统的加速比也就越大,因此系统很适合在大区域战场电磁环境的数字化构建。
5 结论
本文针对利用 PE方程构建战场电磁环境过程中,对应的SSFT算法不易实现并行化的特点,提出了一种基于矩阵转置的并行实现方法。该方法将1维向量构造为2维矩阵,并按行或列分发给并行系统中的各个进程,在各进程中完成绕射项和折射项的计算,降低了并行计算的通信开销,提高了SSFT算法的并行效率。实验结果表明,该方法提高了系统的并行程度和计算速度,具有一定的实际应用价值。
