一类推广的基于进入过程的多险种风险模型

钱晓涛

（福建农林大学金山学院 信息与机电工程系，福建 福州350002）

一类推广的基于进入过程的多险种风险模型

钱晓涛

（福建农林大学金山学院 信息与机电工程系，福建 福州350002）

对索赔到达过程为Poisson过程的单险种风险模型进行推广，讨论了带干扰的基于进入过程且索赔到达过程是复合Poisson－Geometric过程的多险种风险模型，并应用鞅方法得到了该模型满足的Lundberg不等式和破产概率的表达式．

进入过程；破产概率；鞅；复合Poisson－Geometric过程

在经典风险模型中，保险公司的索赔到达过程以及索赔额的大小都与保费的收取没有任何关系，而实际上是受保单到达过程的影响．基于此，文献［1］提出了基于进入过程的风险模型，在该模型中，保险公司只在购买保单顾客的到达时刻向客户收取保费，同时索赔的客户也是从购买保单的客户中选择；但由于该模型的盈余过程不具有独立增量性，因此使其研究具有相当大的难度．为此，文献［2－5］对此模型进行了简化与推广，其中文献［2］考虑的是保险公司只提供一种类型的保单且到达过程服从Poisson过程的模型．但实际上，保险公司提供的大都是多种类型的保单，而且Poisson过程的期望和方差是相等的，因此文献［2］的模型在实践中难以实现．出于上述考虑，本文在文献［2］提出的基于进入过程的风险模型的基础上，考虑由保险公司提供多种类型的保单且保单的到达过程是复合Poisson－Geometric过程时的风险模型，以此为保险公司更好的经营提供理论参考．

1 主要结果及其证明

1．1 模型的建立

考虑风险模型：

其中：u为初始资本；Nl（t）为到t时刻为止第l种类型的保单到达数，Nl（t）～PG（λlt，ρl）；f（Cli）是保险公司对有效期为Cli的第l种类型的保单所收取的保费；f（·）是1个严格单调递增函数；Yli表示第l种类型保单的第i个投保者的索赔额；Tli为购买第l种类型保单的第i个投保者从购买保单到投保事件发生时为止所经过的时间；示性函数I｛Tli≤Cli｝表示只有投保事件发生在保单有效期内时，索赔才能是到t时刻为止发生的总索赔额；B（t）为标准的Brown运动，表示随机因素的干扰作用，其中σ＞0为扰动系数．上述复合Poisson－Geometric过程PG （λlt，ρl）的定义如下：

定义1［6］称母函数为｝的随机变量所服从的分布是复合Poisson－Geometric分布，真正发生记为PG （λ，ρ），其中λ＞0，0≤ρ＜1．

定义2［6］称｛N（t），t≥0｝是参数为λ和ρ的复合Poisson－Geometric过程，如果λ＞0，0≤ρ＜1，且满足：①N（0）＝0；②｛N（t），t≥0｝具有平稳独立增量；③ 对t＞0，有N（t）～PG（λt，ρ），而且

从上述定义不难看出，复合Poisson－Geometric过程的期望与方差并不相等，所以考虑赔付为复合Poisson－Geometric过程的风险模型比赔付为Poisson过程的风险模型更符合实际情况．

假定1 设C，Y，K是3个非负的随机变量，设｛Cli，i≥1｝是与C同分布的1组独立同分布的非负随机变量；｛Yli，i≥1｝是与Y同分布的1组独立同分布的非负随机变量，记E［Y］＝μ；｛Tli，i≥1｝是与K同分布的1组独立同分布的非负随机变量，并记其共同的分布函数为F（·），并且｛Nl（t），t≥0｝，｛Yli，i≥1｝，｛Cli，i≥1｝和｛B（t），t≥0｝相互独立．

假定2 为保证保险公司稳定经营，假定单位时间内的保费收入应大于单位时间内的理赔支出，即要求E（S（t））＞0．因为

与经典风险模型的概念一样，记E［f（C）］＝（1＋θ）μE［F（C）］，其中的θ（θ＞0）称为相对安全负荷系数．另外，定义T＝inf｛t∶t≥0，U（t）＜0｝表示破产发生时刻，ψ（u）＝P（T＜ ∞｜U（0）＝u）表示初始盈余为u时的破产发生概率．

1．2 调节系数的确定

定理1 对于盈余过程｛S（t），t≥0｝，存在函数s（r）使得E［e－rS（t）］＝ets（r）．

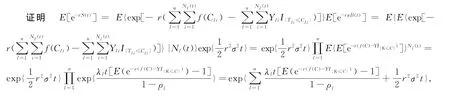
定理2 令s（r）＝0，此方程在r＞0内有唯一正解R，并称R为调节系数．

1．3 破产概率

定义3 对于盈余过程｛S（t），t≥0｝，记Ft＝σ｛S（v）；v≤t｝．

引理1［7］T是Ft的停时．

定理3 ｛M（t），Ft；t≥0｝是鞅，其中M（t）＝e－RU（t），R为调节系数．

证明 ∀0≤v≤t，由盈余过程｛S（t），t≥0｝的平稳独立增量性及定理1和2可得

所以｛M（t），Ft；t≥0｝是鞅．

证明 对于固定的时刻t0＜ ∞，t0∧T是有界停时，由鞅的有界停时定理知e－Ru＝M（0）＝E［M（t0∧T）］．由全期望公式和上式可得

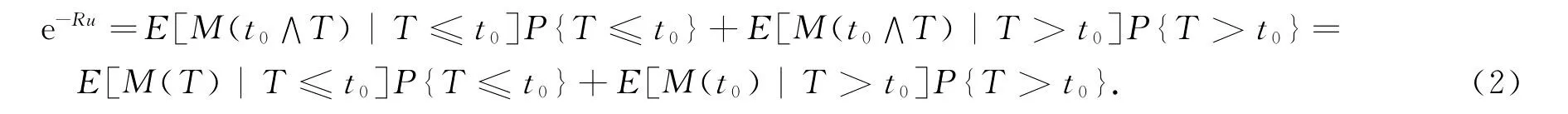
当t0＜T时，U（t0）≥0，从而e－RU（t0）≤1．在（2）式两端令t0→ ∞，由单调收敛定理和Lebesgue控制收敛定理可得e－Ru＝E［M（T）｜T＜ ∞］P｛T＜∞｝＋E［M（∞）｜T＝∞］P｛T＝∞｝，由推广的大数定律可知从而有又因为U（T）＜0，则有e－RU（T）＞1，由上式即得 Ψ（u）≤e－Ru，称之为Lundberg不等式．

［1］ LI Z H，ZHU J X，CHEN F．Study of a risk model based on the entrance processes［J］．Statistic ＆Probability Letters，2005，72（1）：1－10．

［2］ 唐加山，励源芝．基于进入过程带扰动风险模型的破产概率［J］．南京邮电大学学报，2009，21（6）：825－827．

［3］ Paulsen J．Sharp conditions for certain ruin in a risk process with stochastic return on investments［J］．Stochastic Process Appl，1998，75：135－148．

［4］ Xiao H M，Tang J S．Ruin probability of one kind of entrance processes based on insurance risk model［R］．Nanjing：Nanjing University of Posts and Telecommunications，2007．

［5］ 黎锁平，刘琪．投资和干扰具有随机保费的离散风险模型［J］．高校应用数学学报，2009，24（1）：9－14．

［6］ 毛泽春，刘锦萼．索赔次数为复合Poisson－Geometric过程的风险模型及破产概率［J］．应用数学学报，2005，28（3）：419－428．

［7］ Grandell J．Aspects of risk theory［M］．New York：Springer－Verlag，1991．

A generalized multi－risk model based on the entrance processes

QIAN Xiao－tao
（Department of Information and Electrical Engineering，Jinshan College of Fujian Agriculture and Forest University，Fuzhou 350002，China）

A risk model which the compensation arrives to the Poisson process is generalized．We consider the multi－risk model based on the entrance processes and perturbed by diffusion，that is，the arrival of policies is compound Poisson－Geometric processes．Applying the martingale theory，we get the Lundberg inequality and the explicit expression for the ruin probability．

entrance processes；ruin probability；martingale；compound Poisson－Geometric process

O211．6

A

1004－4353（2012）02－0112－03

2012－03－09

钱晓涛（1984—），男，助教，研究方向为随机过程．