环境监测数据处理与分析
2012-10-24严晖
严 晖
(泰兴市环境监测站,江苏 泰兴225400)
环境监测是指间断或连续地测定环境中污染物的浓度,观察、分析其变化和环境影响的过程。在此过程中,对影响环境质量的各种因素进行实时或定期采样、分析测量,以发现异常的因素,定期、定点对环境组成、因子和环境中污染物质的种类、浓度、分布的变化及影响进行监测和分析。
环境监测数据具有代表性和完整性,即所获取的检测数据能较全面地描述污染物的空间分布状态;同时,还具备准确性和可比性,即数据是经过精密仪器采集,并可通过一定的数据处理方法进行可比性分析验证。
目前,环境监测数据的获取方面存在的问题主要包括:数据采集过程中,监测人员在数据筛选或处理时出现人为误差;布控时,未能及时根据监测点附近环境变化而更新布防监控;由于仪器设备过于陈旧而无法进行精密度采集或处理等。产生上述问题的原因主要包括[1]:① 主观原因:监测人员本身业务素质较低,不能科学有效地分析和处理数据,使得部分数据丧失真实性,甚至不能用于评价工作。②客观原因:监测仪器配置和监测站点的布置过于陈旧,并未根据最新环境变化及时更新,使得环境监测数据不具有代表性,造成评价结果的偏差,无法进行科学的分析和处理。
1 分析方法
由于监测数据和污染物空间分布与持续时间等因素有关,故在分析数据时可将数据按周期性规律地进行统计分析,从而得出浓度随时间变化的大致规律;然后根据当地的水文条件、气象变化和地形特征等因素进行综合整理,生成更为详尽的浓度等值线图,便于数据的直观性统计与分析[2]。
1.1 离群数据的分析
环境监测数据获取条件较为复杂,在实际工作中可能由于监测主体或条件变化产生离群值,如何正确区分离群值产生的原因并科学有效地去除离群值,是正确进行评价的重要依据[2]。
1.1.1Q检验法
在同一组数据中,判断最大值或最小值是否为异常值时采用Q检验法——狄克逊(Dixon)检验法:将数据从大到小进行排列,根据测定次数计算Q值:

式中,x2,x1为测定数据。
根据测定数据次数n和显著性水平,查阅Dixon检验统计表,通过比较Q值与临界值,判断x1与xn是否为离群值:若Q≤Q0.05,则可疑值为正常值;若Q0.05<Q≤Q0.01,则可疑值为偏离值,可做保留处理;若Q>Q0.01,则可疑值应予剔除。但该检验方法仅将可疑值与相邻数据进行比较分析,具有一定的局限性[2]。
1.1.2T检验法
对于各组测定数据平均值的一致性检验可采用Grubbs(格拉布斯)检验,即T检验法:将监测数据从大到小排列,并计算其算术平均值和标准偏差s,得到T值[2]。

查阅T检验临界表得T的临界值若则可疑数据x1或xn为异常值,应予剔除;反之,则保留处理。依次反复计算直至无异常数据为止。
1.2 分析结果准确度的检验
1.2.1 平均值与标准值的比较
此方法用于检查监测方法或操作过程是否存在较大系统误差。对标样进行n次监测,再利用T检验法的平均值t比较监测结果与标准值是否存在显著性差异[2]。
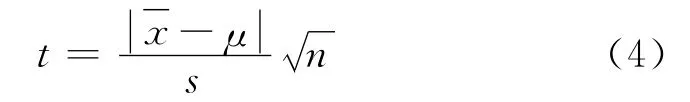
式中,μ为标准值;为监测结果;s为标样测定的标准偏差。根据自由度f和置信度P查得t值,与计算结果进行比较。若计算值大于t值,则存在系统误差;若小于则是由偶然误差引起的。环境监测中置信度一般为95%。
1.2.2 两组平均值的比较
针对同一样品的不同组数据产生平均值误差问题,先假设两组数据的方差无明显差异,计算t值[2],
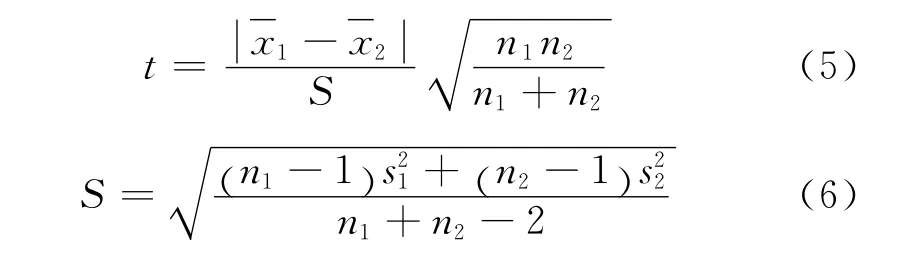
式中,S为合并方差。用P=95%,f=n1+n2-2查表得到t值小于计算值,则存在显著性差异;若大于则无。
1.3 分析结果精密度的检验
用于比较两组数据方差s的一致性,又称F检验:求出两组数据标准方差的平均值和,计算与F分布表中查得一定自由度下的F值进行比较,若大于计算值则存在显著性差异,若无则不存在。
在进行F检验法检验两组数据的精密度是否有显著性差异时,应先确定其类型:单边检验指一组数据的方差不可能小于另一组数据的方差;而双边检验时,其显著性水平为单边检验时的2倍,置信度变为90%[2]。
1.4 等精度检验
对于n′个监测室,用同一标准方法对同一个标准样品作m次监测,测定结果用Cochran最大方差法检验。设各自标准偏差分别为s1,s2,…,sL,(i=1,2,…L),最大值记为smax,计算统计量[2]:

根据给定的显著性水平α,实验室个数n′,测定次数m,从数理统计表得最大方差检验临界值为Ca。当C≤C0.05时,表明各实验室符合精密度要求;当C>C0.01时,表明具有最大标准偏差的实验室精密度不符合要求;当C0.05<C≤C0.01时,表明具有最大标准偏差的实验室精密度具有疑问,需再次考核以确认。
1.5 精密度和准确度统计分析[2]

其中由于∑Ti包括两个类似样品的监测结果从而含有两倍的误差[2],故分母除以2;计算随机标准偏差

若s=sr,则表明实验数据不存在系统误差。当时,需进行方差分析,计算根据显著性水平(0.05)和自由度查表。若表明在95%置信水平时,实验室的系统误差对分析结果的可比性无显著性影响;若表明实验室的系统误差对分析结果的可比性具有显著性影响,应及时采取校正措施[2]。
2 数据融合技术的应用
数据融合技术是指利用计算机对按时序获得的若干观测信息,在一定准则下加以自动分析、综合,以完成所需的决策和评估任务而进行的信息处理技术。
人类通过人体器官感受外部信息,转换成生物电,并通过人的中枢神经传送到大脑进行综合分析处理,然后对外部环境进行判断和控制。而多传感器数据融合的基本原理就如同人脑综合处理所感受的信息:利用多个传感器感测外部环境信息,再把多个传感器的数据根据某种准则进行组合,以获得对被测对象的一致性解释和描述,从而得出更为准确的可信的结论。
面对大量的环境监测任务,如何科学有效地获取数据信息是最为关键的一步,融合技术为我们提供了强有力的支持,然而这些数据在采集、利用过程中,由于传感器采集数据的特征性差异,造成数据存在模糊性、互补性或矛盾性。如何有效并准确的处理传感器所采集的数据是以后研究的重点,而这必将为环境监测数据研究带来重大性突破。
2.1 融合模型
20世纪80年代,代表性的数据融合模型包括[3-6]:英国情报环模型、美国JDL模型和Boyd控制环模型。20世纪90年代提出的“改进的JDL模型”[3]在军事领域应用十分广泛,还有将融合过程划分成观测、定位、决策、行动及传感器管理等阶段,并组成一个大循环的“综合模型(Omnibus Model)”[6]等。但由于上述模型均未引入自学习和多级反馈机制,使得其自适应性和自我完善功能有待提高。
目前,融合算法主要有Kalman滤波器的改进方法[7-8]、“数值-语言”混杂条件下的“知识发现和数据挖掘(Knowledge Discovery and Data Mining,KDDM)[7]”方法与面向分布式数据融合的支持向量机(Support Vector Machine,SVM)方法等。
2.2 应用举例
由于Kalman滤波方法是解决最优化滤波问题的经典方法,故消除被噪声污染的观测信号中的噪声影响,常将Kalman滤波方法用于环境采样数据真实值的估计。在此本文以大气监测为例,简单探讨Kalman滤波方法在环境监测方面的应用[9]。
(1)建立大气变化状态转移矩阵。根据环境科学相关领域知识,结合传感器采集的大气参数,建立关于这些参数的大气参数状态转移矩阵。利用该矩阵,研究各项大气参数的变化情况。
(2)根据式(1)中得到的观测目标属性特征,对来自各传感器的,反映不同污染现象的观测数据进行分析,分解出反映各种不同的污染现象的参数向量值。
(3)根据大气变化状态转移矩阵,利用各传感器采集的大气参数观察值,对各大气采样站点的环境进行最优化估计,得到各项参数的最优化估计值。
3 结 语
(1)对环境监测数据的可疑值判断和取舍方法进行了研究,同时还探讨了监测结果的统计方法和实验室监测质量的统计方法。
(2)简单展望了未来数据融合技术在环境监测方面的应用,并以大气监测为例进行分析。
[1]叶 萍.浅议环境监测数据的审核[J].中国环境管理干部学院学报,2010(2):45-46.
[2]马彦峰,张 勇.环境监测数据结果评价[J].环境保护科学,2010(1):23-25.
[3]Linas J,Bowman C,Rogova G,et al.Revisiting the JDL data fusion model Ⅱ [C]//Proceedings of the Seventh International Conference on Information Fusion.Stockholm,Sweden:[s.n.],2004,2:1218-1230.
[4]Kalandros M K,Trailovic L,Pao L Y,et al.Tutorial on multisensor management and fusion algorithms for target tracking[C]//Proceedings of the 2004American Control Conference.Boston,Massachusetts:[s.n.],2004,5:4734-4748.
[5]何 友,王国宏,陆大金,等.多传感器信息融合及应用[M].北京:电子工业出版社,2000.
[6]潘 泉,于 昕,程咏梅,等.信息融合理论的基本方法与进展[J].自动化学报,2003,29(4):599-615.
[7]Gao J B,Harris C J.Some remarks on Kalman filters for the multisensor fusion[J].Information Fusion,2002,3(3):191-201.
[8]Sun Shuli,Deng Zili.Multi-sensor optimal information fusion Kalman filter[J].Automatica,2004,40(6):1017-1023.
[9]邵 斌,蒋云良,张建宏.面向环境监测数据的融合方法研究[J].心智与计算,2008,2(1):42-47.
