超重核区的双幻性质研究

黄亚伟

（文山学院 数理系，云南 文山 663000）

近几年SHEs（superheavy elements）的理论研究非常的热烈。为寻找稳定岛和下一个双幻核，很多成功的理论模型被应用到SHEs性质的研究中，并给出了种种预言。按壳模型理论，208Rb之后的下一个双幻核应为310126184，但大量理论预测的结果并非完全一致，有的甚至给出相反的结果。例如，完全自洽的Skyrme-Hartree-Fock（SHF），相互作用采用SkI4、SKM、SkP等［1-2］的计算结果，认为N=184确实是下一个中子幻数；RHB采用Sly4力的计算［3］、宏观微观（MM）模型［3］和最近Lublin-Strasbourg液滴（LSD）模型［4］的计算，也得到同样的结果。但绝大部分的相对论平均场（RMF）模型［2-3］（包括轴对称RMF和形变RMF［5］）以及SHF采用SkI3力的计算结果［2］，都不支持此观点。对下一个质子幻数则存在更大的争议，应用各种理论模型预测的结果相当分散。只有极少数研究结果（SHF中采用SKM、SkP力［2］和密度无关零程对力SHF以及MM的部分计算结果［6］）认为Z=126存在幻结构，其它的则分布在Z=106、108、110、112、114、116、120、138等。稍多的是支持Z=114，如SHF采用SkI4 力［1-2］、RHB 采用 Gogny力［7］，RMF 中 TMAL力［2］和轴对称 RMF［5］、以及宏观微观（MM）模型［3］等均显示在Z=114存在明显的壳结构；但更多SHF采用除SkI3力外的计算结果［1-2］、HFB采用Sly4力的计算［3］以及其它的RMF（如NL-Z2、LP-40等）和形变的RMF等的计算预测，对这个数目没有强烈的壳的效果。此外，再考虑形状因素，应用宏观-微观模型的理论计算预言的形变双幻核和球形双幻核分别是270Hs和298114［10-11］，前者在实验上已发现在N=162和Z=108附近原子核稳定性的增强，某些相对论平均场理论计算也给出相同的结果，但要确认为双幻核证据显得不足。另外，应用SHF方法计算依照所选参数的不同预测298114、292120或310126为球形双幻核［7,10］。本文通过结合能计算α衰变能和应用V-S公式计算α衰变寿命，并采用连续介质模型和Strutinsky壳修正能量计算以及比较上述文献研究结果认为，核298114是SHEs区球形双幻核的最佳候选者。

1 α衰变能量与寿命

SHE的两种主要衰变模式是α衰变和自发裂变，它们之间的竞争决定了SHE衰变方式和寿命。实验上已知114核（除286114外）的衰变模式以α衰变为主。α衰变中两个重要的物理量为α衰变能与α衰变寿命Tα。α衰变能Qα（单位为MeV）一般由下式得到：

Z代表α衰变母核的质子数。α衰变寿命Tα则采用唯象的Viola-Seaborg公式来计算［11］：

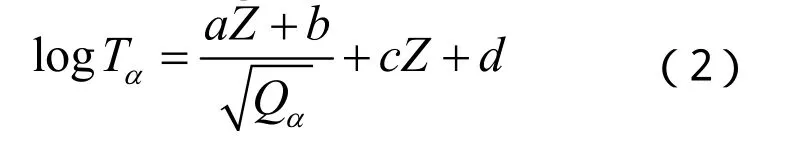
式 中 ：a=1.81040， b=-21.7199，c=-0.26488，d=-28.1319［6］，得到的Tα单位为秒。由于该公式忽略了许多结构效应，如形变、组态改变等，故只能用来进行粗略估算。

由LSD模型得到的超重偶偶核在100≤Z≤122、150≤ N ≤ 192范围内的 Qα值变化［3］显示，SHEs的α-衰变能随N的变化范围随着Z的增大而逐渐上移，由168-144Fm的5.5～8.5 MeV变化到192-162122的13.5～15.5 MeV；而对同Z的同位素，α-衰变能随N的增大逐渐下降，但在112≤Z≤122范围内的SHEs均在N=184处有一Qα较大的向上跃变，其值ΔQα≈0.6～1.5 MeV，表现出强烈的闭壳结构；同样地，在100≤Z≤116范围内N=162处有一Qα较小的向上跃变，其值ΔQα≈0.2～0.5 MeV，也表现出一明显的支闭壳结构（该支闭壳在HFB-Sly4模型结果中更显著，ΔQα达到0.5～1.1 MeV［11］）。文献［12］也给出同样的结果。

再看SHEs的衰变寿命。对α-衰变和自发裂变两种衰变模式中，112≤Z≤126、178≤N≤186区二者详细的计算结果比较［11］认为，Z=114,116,118三个核的对应两曲线没有太大差别；而Z=120的Tsf显著减小；Z≤112时，Tα逐渐延长而接近Tsf，且二者都呈明显增大趋势。LSD计算结果显示，296112184的α-衰变寿命最长；而294110184和296112184的自发衰变寿命最长。即SHEs中最稳定的是296112184［3］。

从α-衰变的寿命来看，三条α-衰变链实验值显示从118往下的偶Z核，logT1/2呈递增态势，其中两条在116 logT1/2稍大，另一条在114 logT1/2稍大，也不足以证明质子幻数Z=114。另外，形变重核最长半衰期是1000 s，而球形SHEs为30年。有趣并值得注意的是，最长半衰期没有出现在有人提出的球形双幻核184298114，而是在Z=110和N =182。文献［13］认为，这是由于随元素数的增加Qα值不断增长的结果。再从RMF的计算结果［5］来看, TMA力理论值显示的衰变寿命,288114比附近偶偶核长很多,似乎具备了幻数的资格,但实验值却否认了这一结论。而NLZ2力理论值本身就显示不出哪一个Z更占优势。

宏观-微观模型计算结果则明显显示了中子数为N=162和184及质子数为Z=100和114出现显著的幻壳结构［11］。另外该文还给出N=184时Tsf与Tα随Z=104～120的变化特性，可以看出，Tα-Z关系近似为一直线，Tsf随Z的增加呈递减态势。Tsf-Z曲线在Z=114显现一折点，表现出Tsf与Tα间隙最大。这说明，核Z=114稳定性的壳效应是由Tsf决定的，Tα对此几乎没什么贡献。

本文计算结果见图1和图2。由图1可见，Qα计算值基本与实验值吻合。当N≥178时，计算的Z=114与116两条曲线与邻近间隔相比有较大的间距，显示出Z=114可能的质子壳特征。由于没有N≥176的实验数据，所以无法证实。图2由S-V公式计算的比较半衰期LogTα也同样显示当N≥178时，Z=114有较大的值，具有质子壳特征。

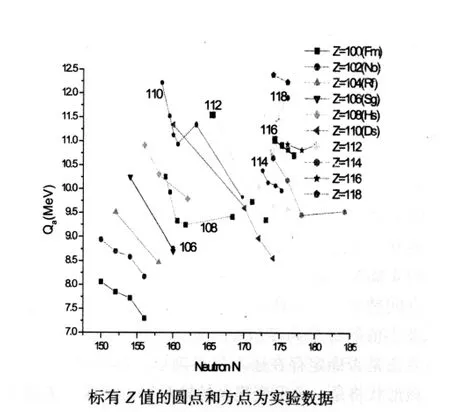
图1 Qa计算值与实验数据比较图

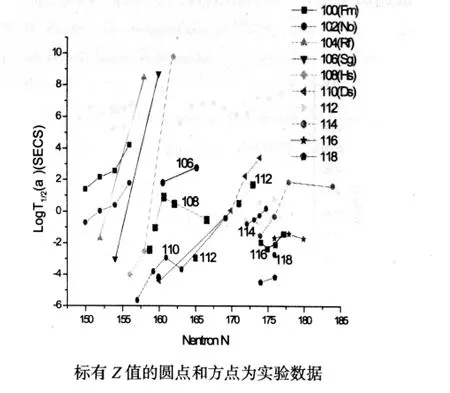
图2 LogTa计算值与实验数据比较图

2 形状及其变化

SHEs由于中子数的大大增加，其形状演变将发生很大的变化。文献［5］通过计算认为，长椭球形变对SHEs基态很重要。由TMA力得到的四极形变曲线显示：在SHEs有形状共存，并认为288114和298114基态均为β2=0.45的形变核。而280110、284112的基态形变为0.18和0.44。采用SHF方法Sly4力的计算结果显示，SHEs不同程度存在着球形、轴对称形变和三轴形变。也有应用SHF方法和RMF模型得到162108为形变核，298114为球形核［1-2］。

应用连续介质模型对270108、298114、306118核进行一维势能计算，并考虑一些必要的修正，其结果见图3：核298114基态能量最低点相当深，围绕能量最低点的势垒特别高，接近10 MeV。这表明298114基态是对应β2=0的球形；另一方面势垒的高度决定着自发裂变寿命，势垒越高，核的自发裂变概率越小，核的稳定性也就越好，说明了298114基态是一稳定性很好的球形核。文献［11］的计算表明，298114附近原子核的自发裂变寿命比270Hs附近的核大约长10倍，与本文结论一致。从图中还可看出，除了β2≈0的基态以外，298114核在β2≈0.43附近还有一个能量极小点，其能量值比基态能量值高出约4 MeV，这一极小点就是最近SHEs中研究的热点问题之一—SHEs的超形变现象［9］。显然，第二极小值的势垒高度较低，约1.8 MeV，故这一超形变态是否稳定存在还不是很确切。如果存在，此时核形状将是一个形变很大的轴对称长椭球。关键是，在如此大的形变下，SHEs更倾向于裂变，而不是形成超形变态。

图3 壳修正能量Eshell与四极形变参数β2关系图

显然，核270108基态是一个β2≈0.25的长椭球，第一势垒高度略大于7 MeV，由于该最大值Emax对应着超形变β2≈0.50，因而Emax成为270108稳定的阈值，一旦形变能超过Emax，该核将发生裂变。对于核306118，其势能曲线形状与298114类似，基态也是球形。但由于基态两侧的势垒高度较低，很容易发生形变，特别是β2＜0一侧曲线平坦，表现出软性核特征，易形变为扁椭球。

3 壳能级结构

能级分布和壳结构是原子核结构研究中最基本的问题之一，大量的计算和与实验的比较已经表明Woods-Saxon势能很好的给出单粒子能级分布。由LDS模型计算得到的SHEs基态总壳能量Eshell等高线图显示［3］，存在三个极小值区：第一个位于N=152较轻的SHEs区并在Z≥110时消失，Eshell约为-8.5 MeV；第二个处于支闭壳N=162附近，最低能量为（-10 MeV）。这一强烈的壳效应形成在以270Hs为中心的形变超重核岛上，其稳定性已被最近的实验证实；最后一个最小值区（-9.5 MeV）显示在298114及其附近。这给出了幻壳结构大致分布的区域。计算的质子、中子单粒子能量图［13］显示：Z=82、114表现出较大的壳能隙，说明在Z=114确实存在球形闭壳，另一个较小的闭壳显示在Z=124；中子较大的闭壳显示在N=120、164、184，较小的一个显示在N=178。HFB-Sly4模型的质子与中子单粒子能级计算结果［6］显示，Z=108、116、118、122存在质子闭壳，N=162、174、184存在中子闭壳。文献［3］12种模型计算的 εp、εn，分别显示了Z=114、120、126、138和N=172、184出现较大的闭壳。

基于Strutinsky壳修正能量Eshell的计算结果，显示在图4。可见，质子Eshell的最小值落在114，说明Z=114最为稳定，具有闭壳的特征；而Eshell随N的变化，对Z=110、112最小值显示在N=184；对Z=114、116最小值显示在N=182；而对Z=116、118，Eshell的最小值又显示在N=180。可见Strutinsky壳修正能量不能给出明确的中子闭壳。

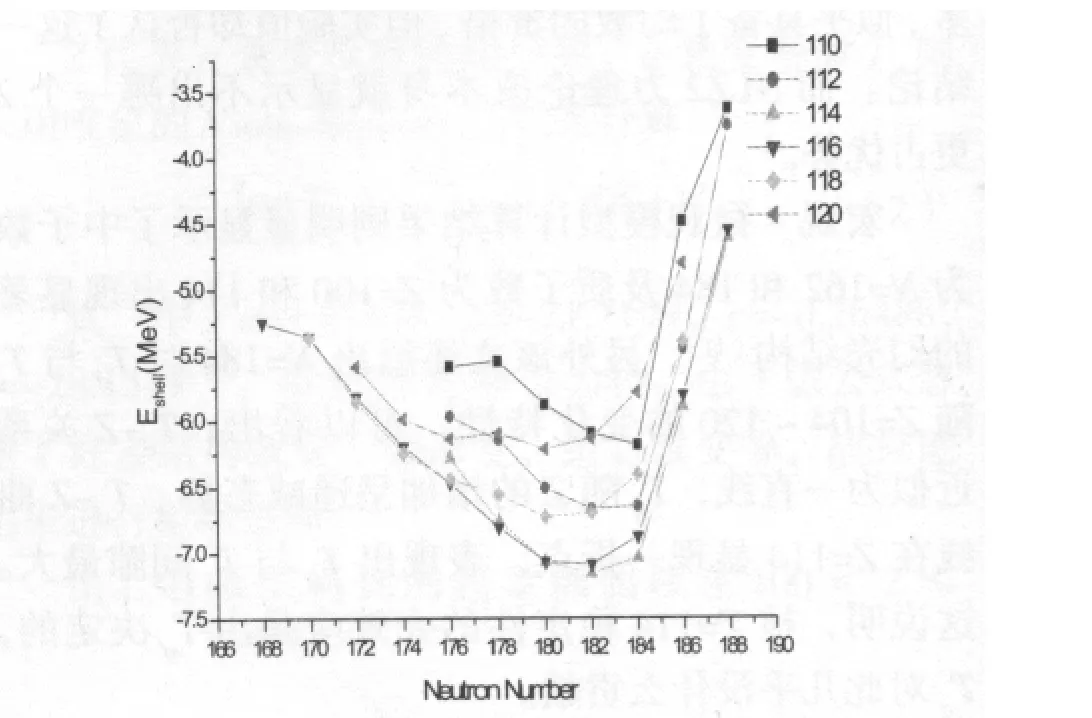
图4 基于Strutinsky计算的不同超重核壳修正能量Eshell变化图

4 结语

综上所述，基于本文以及多种理论模型、方法的计算结果显示：对于SHE区，中子数N=184反映的强闭壳是确信无疑的，可以确定为这一区域的中子幻数；而质子数Z=114是否为闭壳虽出现较大争议，但更多的理论模型和我们的计算结果给予了很好的支持。问题的焦点应该是：该闭壳只是一个支闭壳还是一个真正的主闭壳？种种迹象表明，它至少是一个支闭壳。由于在SHE区已没有更强烈的闭壳出现，不妨把它视为主闭壳。这一观点如果成立的话，我们就可以说：在SHE区，球形的中子与质子壳分别是Z=114和N=184，它们构成了SHE区的中子、质子幻数，298114核也就成为SHE区中唯一的一个球形双幻核。

［1］T.Bürvenich,K.Rutz, M.Bender, et al.Superheavy nuclei in deformed mean-field calculations［J］.Eur.Phys.J.A.,1998，3：139.

［2］K.Rutz, M.Bender, T.Bürvenich, et al.Superheavy nuclei in self-consistent nuclear calculations［J］.Phys.Rev C,1997（1）：238-243.

［3］A.Baran, Z.Łojewski, K.Sieja, et al.Global properties of even-even superheavy nuclei in macroscopic-microscopic models.［J］.Phys.Rev C, 2005, 72:044310.

［4］A.Baran, Z.Łojewski, and K.Sieja, Ground-state properties of superheavy elements in macroscopic-microscopic models，Eur.Phys.J.A ,2005（s01）:611.

［5］Zhongzhou Ren.Shape coexistence in even-even superheavy nuclei［J］.Phys.Rev C, 2002, 65 ： 051304.

［6］S.Ćwiok, W.Nazarewicz, P.H.Heenen, Structure of Odd-N Superheavy Elements［J］.Phys.Rev.Lett.,1999,83:1108-111.

［7］M.Sharma, G.Lalazissis, J.König, and P.Ring.Isospin Dependence of the Spin-Orbit Force and Effective Nuclear Potentials［J］.Phys.Rev.Lett., 1995,74:3744-3747.

［8］Y.T.Oganessian et al.Measurements of cross sections for the fusion-evaporation reactions244Pu（48Ca,xn）292−x114 and245Cm（48Ca,xn）293−x116［J］.Phys.Rev.C, 2004,69:054607.

［9］W.D.Myers, W.J.Swiatecki.Nuclear equation of state［J］.Nucl.Phys.c, 1998（6）：3020-3025.

［10］M.Bender, K.Rutz, P.-G.Reinhard, et al.Shell structure of superheavy nuclei in self-consistent mean-field models［J］.Phys.Rev.C, 1999, 60:034304.

［11］R.Smolańczuk.Properties of the hypothetical spherical superheavy nuclei［J］.Phys.Rev C, 1997（2）：812-824.

［12］M.Bender.α-decay chains of289114175and293118175in the relativistic mean-field model［J］.Phys.Rev C, 2000, 61 ：031302.

［13］S.Hofmann, G.Münzenberg.The discovery of the heaviest elements［J］.Rev.Mod.Phys., 2000,72:733-767.