基于灰色粗糙集理论的风电机组传动链智能故障诊断方法
2012-10-23蒋维
蒋维
(中国水利电力物资有限公司,北京 100045)
风电是世界上公认的最接近商业化的可再生能源技术之一[1]。据全球风能理事会(GWEC)的统计数据显示,1996年至2009年期间,世界风电累计装机的平均增长速度达到了28.6%,风电已成为世界上增长最快的可再生能源[2]。随着风能的快速发展和大规模风电机组的投入运行,且由于大部分机组安装在偏远地区,负荷不稳定等因素,我国不少风电机组都出现了运行故障,直接影响了风电的安全性和经济性。为保持风电的长期稳定发展,增强它与传统能源的竞争力,必须不断降低风电的成本(包括制造安装成本和运行维护成本)。旋转机械在风电机组中占有很大的部分,从叶片、主轴承到齿轮箱再到发电机,整个传动链都是以旋转形式传递着机械能。风电机组速比较大、多轴系,且包含低速重载的叶轮轴、高速轻载的电机轴及多个关系复杂的齿轮和轴承零部件;又由于其安装地理位置的特殊性、运行环境的复杂性及运行工况的波动性等特征,使得反映机组健康状况的状态参量以较为复杂的关联形式呈现[3]。因此,风电机组的状态检测和故障诊断显得尤为重要,是保证机组长期稳定运行和安全发电的关键。
基于灰色系统理论的设备故障诊断方法与基于粗糙集理论的设备故障诊断方法得到广泛应用[4-6]。基于灰色系统理论的设备故障诊断是通过对灰色关联度的分析,研究设备当前运行状态与各种典型故障状态特征间的相关性,从而确定设备的故障原因。这种故障诊断方法由于无法区别特征参数是相关的还是独立的,往往将所有特征参数一一罗列,导致工作量大大增加。基于粗糙集理论的设备故障诊断方法是针对设备各种故障的特征参数构成的决策表,利用粗糙集优越的约简能力,对决策表中冗余特征参数约简,再从约简的决策表中提取规则,从而进行故障诊断。但是,粗糙集理论不能处理连续数值,应用粗糙集理论时必须先对连续数值进行离散化处理。由于灰色系统理论与粗糙集理论的理论基础不同,在处理不确定性复杂系统时有很强的互补性[7],因此探讨2种理论的结合,并应用于风电机组的故障诊断中,具有重要的理论意义和应用价值。
1 系统理论与方法
1.1 灰色系统理论
在灰色系统理论中,设参考序列X0和比较序列Xi分别是
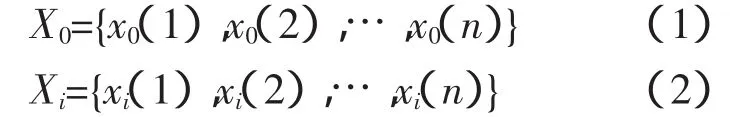
若参考序列X0和比较序列Xi在k点的关联度系数为ξi(k),则参考序列X0和比较序列Xi的关联度为
在取得了参考序列X0和比较序列Xi的关联度后,则根据关联度的大小确定参考序列X0和比较序列Xi的相关程度,关联度越大说明两者越相关联,关联度越小则说明两者越不相关联。关联系数的计算是灰色关联分析的关键,直接决定着灰色关联分析结果的准确性。用于关联度分析的各特征参数具有不同的量纲,在计算关联度之前,需要对这些特征参数进行无量纲化处理。对于抽象系统,由于是时序模型,参考序列和比较序列是按时间排列的一组数,其量纲相同,无量纲化处理可以采用横向初始化或横向均值化。在设备故障诊断过程中使用灰色关联度分析方法时,其物理模型、几何意义和计算方法都有一些新的特点[8]。风机故障诊断模型属于非时序模

1.2 粗糙集理论
粗糙集理论是波兰学者Pawlak Z在1982年提出的,是一种刻画不完整和不确定信息的数学工具,它能有效地处理不精确、不一致、不完整的数据信息,发现数据间潜在关系,从而提取有用知识,以获得知识的简要表达[10]。
1.2.1 相关的5个定义
1)设非空有限集合为U和A(其中U为论域,A为属性域),对于每个属性a∈A,存在属性值集合Va={a(x)|坌x∈U},称S={U,A}为信息系统。若A=C∪D=准,且C∩D(其中C为条件属性集),D为决策属性集,则称S={U,C∪D}为决策系统。
2)信息系统S={U,A},设C哿A,称二元等价关系IND(C)={(x,y)∈U2|a(x)=a(y),坌a∈C}为论域U上C的不可分辨关系。
3)设C哿A,X哿U,则X的C上近似C-(X)和下近似C-(X)分别为
C-(X)=∪{Y∈U/C|Y∩X≠准},
C-(X)=∪{Y∈U/C|Y哿X}
习惯上把POSc(X)=C-(X)称为X的C正域,NEGc(X)=U-C-(X)称为X的C负域。BNc(X)=C-(X)-C-(X)为边界域。
4)对于信息系统S={U,A},设a∈A,当IND(A)=IND(A-a),称a是A中可省略的,否则a是A中不可省略的。IND(A)=IND(B),则称B是A的简化。A中所有不可省略属性的集合,称为A的核,记为core(A)=∩red(A),其中red(A)表示A的所有简化。
5)对于决策系统S={U,C∪D},设属性c∈B,其中:B哿C,POSB(D)=∪型,参考序列和比较序列是由不同参数排列的一组数,其量纲不同,无量纲化处理不能采用横向初始化或横向均值化,只能采用纵向初始化或纵向均值化。由于关联度的计算方法是针对时序模型提出的,因而在众多的关联度计算方法中,大多数计算方法不适用于非时序模型,经分析,邓氏关联度和改进关联度适合非时序模型,因此在故障诊断中,运用关联分析方法时,仅能采用邓氏关联度或改进关联度[9],本文采用前者。邓氏关联度的关联系数为,当POS(BD)=POS(B-c)(D)时,称c是B中D不可省略的。当B中的每个属性c都是D中不可省略的,则称B为D独立的。当B为C的D独立子集,且PODB(D)=POS(CD),则称B为C的D简化。
1.2.2 约简
决策表的约简就是化简决策表中的条件属性,化简后的决策表具有简化前的决策表的功能,但简化后的决策表具有更少的条件属性。
1)决策系统S={U,A},其中A=C∪D,且C∩D=准,C为条件属性集,D为决策属性集,U={x1,x2,…,xn},C={c1,c2,…,cm}D={d},可分辨矩阵是n×n矩阵,其第i行第j列元素

2)由可分辨矩阵MD唯一地确定一个分辨函数F,分辨函数是一个布尔函数,对于每个属性c∈C,如果区分对象x和y的所有属性集合c(x,y)={c1,c2,…,ck}≠准,指定一个布尔函数c1∨c2∨…∨ck,用Σc(x,y)来表示,分辨函F数定义为

2 基于灰色理论与粗糙集理论的风电机组传动链智能故障诊断方法
2.1 融合灰色粗糙集推理方法的流程
本文将灰色系统理论与粗糙集理论结合起来,应用于风电机组传动链系统的故障诊断中。它将灰色关联分析和粗糙集合并,其中灰色关联分析方法利用灰色关联度确定设计属性与实际值的差距,若灰色关联度大,说明差距小,取设计属性数据;反之,取实际值。粗糙集的推理过程是利用决策表进行约简。在应用于风电机组传动链复杂系统时,灰色粗集推理方法实现的首要问题是获取信息。
2.2 故障诊断数据来源
本文刊发了“风力发电机组机械状态在线监测与诊断分析系统”(CWEME-Windit系统,如图1所示)能够连续监测风电机组运行过程中的振动、冲击、晃度、转速、负荷等参数,自动存储振动、冲击、波形等有价值的数据,并能自动计算机组各部件的故障特征频率;加速度传感器直接测量机组主轴承、齿轮箱、发电机的振动;每台机组共安装8只加速度传感器。主要布置在主轴、齿轮箱和发电机组上。其中在主轴轴承座、齿轮箱输入轴处各安装一只专用低频加速度传感器,齿轮箱外齿圈外壳、输出轴箱体外壳处以及发电机前后轴承座等处各布置一只振动加速度传感器,用于全方位监测风力发电机组的振动状态。

图1 CWEME-Windit系统界面Fig.1 CWEME-Windit system interface
2.3 风电机组传动链故障诊断的具体步骤
1)根据学习样本集,对条件属性值进行无量纲化处理,从而形成决策表,然后利用粗糙集理论进行约简,形成最小条件属性集。学习样本集中的条件属性值可以采用纵向初始化或纵向均值化。对学习样本集中的条件属性值无量纲化处理后,可以很方便地构成决策表。决策表中含有很多条件属性,不可避免地存在着冗余的条件属性,可以采用式(2)构造决策表的可分辨矩阵,在完成可分辨矩阵的构造后,再利用式(5)确定其分辨函数。由于分辨函数的极小析取范式中的所有含取式是条件属性关于所有决策属性的简化集,因此,可以通过求分辨函数的极小析取范式中的含取式来对条件属性约简,从而求得最小条件属性集。
2)形成最小条件属性集后,需要判断各条件属性的重要性。
3)属性子集P哿A的信息熵为

式中,U/IND(P)={X1,X2,…,Xm};P(Xi)=|Xi|/|U|(i=1,2,…,m);|U|表示集合U的“势”;|Xi|表示集合Xi的“势”。
4)信息系统S={U,A},属性a∈A的重要性定义为
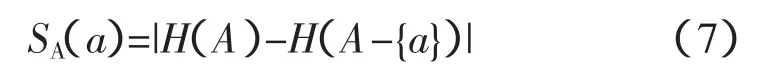
当时SA(a)≥0,属性a在A中是必要的,等于0时,是冗余的。运用式(4)和式(5),可以求的最小条件属性集中各个条件属性的重要性。
5)计算待检模式与各标准故障模式的关联度,从而判断故障原因。
确定了各属性的重要性后,可按下式确定在关联度计算中各属性的权重。
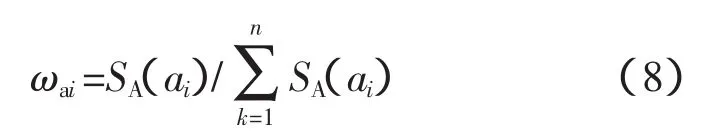
然后,按式(1)计算待检模式与标准故障模式的关于属性ak的关联系数ξi(ak)。
6)为计算简便,利用Matlab定制开发了融合灰色粗糙集方法求解器,如图2所示。

图2 基于灰色理论与粗糙集方法的matlab求解器Fig.2 Matlab solver based on grey theory and rough set method
3 应用实例计算
CWEME-Windit系统拥有强大的轴承数据库,可准确地识别出轴承的内圈故障特征频率、外圈故障特征频率、保持架故障特征频率和滚动体故障特征频率,并及早地发现轴承的各种早期损坏状态,提前制定维修方案和计划,确保设备安全稳定运转。风电机轴系振动信号经过小波包分解后各频带能量特征向量,故障类型有7种,特征参数集有13个,(限于篇幅,原始故障样本表略去)。表1为标准故障发生时各特征参数值及待检模式。通过对特征参数无量纲化处理得到标准故障发生时,各特征参数值如表1所示。这里假定轴承常见故障集为{F1,F2,…,F7},特征参数集为{Z1,Z2,…,Z13},在求得最小特征参数集后,计算各特征参数的重要性。
{U/IND{d1,d2,d9,d10}={{F1},{F2,F3},{F4},{F5},{F7}}
{U/IND{d2,d9,d10}={{F1,F6},{F2,F3},{F4},{F5},{F7}}
{U/IND{d1,d9,d10}={{F1},{F2,F3},{F4},{F5},{F6,F7}}
{U/IND{d1,d2,d10}={{F1},{F2,F3,F5},{F4},{F6},{F7}}
{U/IND{d1,d2,d9}={{F1},{F2,F3,F4},{F5,F6},{F7}}
由式(6)、(7)计算得d1,d2,d9,d10的重要度分别为:0.2173,0.2173,0.2387,0.4291。再按照式(8),得各特征参数的权重系数向量w=(0.1682,0.1682,0.2573,0.4306),该轴承在运行过程中d1~d13的值如表1所示。

表1 标准故障发生时各特征参数值及待检模式Tab 1 .The feature parameter values and modes when the standard fault occurs
由于{d1,d2,d9,d10}是最小特征参数集,因此按4个参数,用上述方法计算出它与标准故障序列的关联度为:0.9631,0.5247,0.5247,0.4829,0.6538,0.8216,0.8183。根据最大关联度原则,可以判断故障原因为F1。单纯通过灰色关联度计算,得到计算结果与本方法计算结果完全一致。但需要利用所有的特征参数,而在本文中,只用了4个特征参数,大大减少了计算时间,提高了诊断效率。同时,由于去除了冗余的特征参数的干扰,诊断的准确性也可进一步提高。
4 结语
随着风电在世界范围内的快速发展,如何降低发电成本、保证机组的运行可靠性已成为一个亟待解决的问题。风电机组是一个复杂的机电综合系统,往往征兆与故障之间存在多种映射关系,故障诊断仍存在较大的困难。本文将灰色系统理论与粗糙集理论有机地结合应用于风电机组传动链轴承故障诊断中。实例验证表明,该方法是一种行之有效的方法,为智能故障诊断提供了理论基础。
[1] 李海波,卢绪祥,李录平,等.风力机叶片动力特性实验台设计[J].热能动力工程,2012,27(1):117-121.LI Hai-bo,LU Xu-xiang,LI Lu-ping,et al.Journal of engineering for thermal energy and power[J].Journal of Engineering for Thermal Energy and Power,2012,27(1):117-121(in Chinese).
[2] 蒋东翔,洪良友,黄乾,等.风力机状态监测与故障诊断技术研究[J].电网与清洁能源,2008,3(24):40-44.JIANG Dong-xiang,HONG Liang-you,HUANG Qian,et al.Condition monitoring and fault diagnostic techniques for wind turbine[J].Power System and Clean Energy,2008,3(24):40-44(in Chinese).
[3] 张礼达,陈荣盛,张彦南,等.风力机风轮叶片振动特性分析[J].电力科学与工程,2009,25(11):24-27.ZHANG Li-da,CHEN Rong-sheng,ZHANG Yan-nan,et al.Study on wind turbine rotor blades dynamic characteristics based on ANSYS[J].Electric Power Science and Engineering,2009,25(11):24-27(in Chinese).
[4]FRANCISEH,SHENLX.Faultdiagnosisbasedonrough set theory[J].Engineering Application so Far Artificiality Intelligence,2003,16(1):39-43.
[5]WANG Q H,LI J R.A rough set based fault ranking prototype system for fault diagnosis[J].Engineering Applications of Artificial Intelligence,2004,17(8):909-917.
[6]WANGMH,HUNGCP.Novel Grey model for the prediction of trend of dissolved gases in oil-filled power apparatus[J].Electric Power Systems Research,2003,67(1):53-58.
[7] 罗党,刘思峰,吴顺祥.灰色粗糙组合决策模型研究[J].厦门大学学学报,2004,43(1):26-30.LUO Dang,LIU Si-feng,WU Shun-xiang.Research on the grey rough combined decision making model[J].Journal of Xiamen University,2004,43(1):26-30 (in Chinese).
[8] 牛丽仙,苑津莎,张英慧.基于粗糙集和支持向量机的电力系统短期负荷预测[J].电力科学与工程,2010,26(2):32-35.NIU Li-xian,YUAN Jin-sha,ZHANG Ying-hui.Short-Term load forecasting based on algorithms of rough sets and support vector machine[J].Electric Power Science and Engineering,2010,26(2):32-35(in Chinese).
[9] 苏蓬,苑津莎,安晓玲.基于粗糙集理论的变压器故障诊断方法[J].电力科学与工程,2008,28(3):56-59.SU Peng,YUAN Jin-sha,AN Xiao-ling,et al.Diagnosis method of transformer faults based on rough set theory[J].Electric Power Science and Engineering,2008,28(3):56-59(in Chinese).
[10]韩绪鹏,李道霖,戴迪.基于粗糙集和神经网络的电力系统操作点状态评估[J].电网与清洁能源,2012,28(1):16-20.HAN Xu-peng, LI Dao-lin, DAI Di.Power system operating point state assessment based on rough set and neural network[J].Power System and Clean Energy,2012,28(1):16-20(in Chinese).
