具有交期约束的非同质顾客并行机竞争调度

王长军，贾永基

（东华大学 旭日工商管理学院，上海 200051）

具有交期约束的非同质顾客并行机竞争调度

王长军，贾永基

（东华大学 旭日工商管理学院，上海 200051）

考虑面向具有交期要求的非同质顾客的并行机调度问题，其中，不同顾客具有不同等待敏感程度，且具有各自的交期约束.为此，采用非合作博弈建立描述该问题的模型，并提出一种包含松弛、可行化和交互协调三步的启发式算法.算例仿真进一步阐述和验证所提方法的有效性.

并行机调度；非同质顾客；交期；启发式算法

顾客对于等待是敏感的［1］，等待的情况将直接影响顾客对于服务的评价［2］.为此，按照顾客对于等待的敏感程度，为其提供产品或服务，是企业应当具有的一项重要的能力.但是，不同顾客会因为经营模式、产品或服务对其重要程度等差异，而呈现明显不同的等待特性.比如，对于采用精益运作模式的顾客而言，最常见的越快越好的规则未必适用他们.在出口与内需共存，实物渠道和电子渠道并重的今天，不同的时间效用已成为顾客诉求差异化的一项重要体现.这自然会给供应链带来影响，也需要提供产品或服务的企业做出相应的调整.

现有运作研究多假定顾客为同质（homogeneity），但也开始有研究者关注不同顾客具有不同时间效用 （time utility，后简称“时效”）函数［3］，即非同质顾客的情况.如文献［4］在供应方为单机的情况下，考虑两类分别具有不同时效函数的顾客，并证明这样的问题为非确定性多项式困难（non－deterministic polynomial－hard，NP－hard）.文献［5］深入研究了非同质顾客给全局最优的实现带来的影响，即无秩序代价（price of anarchy），给出了不同情况下的明确上下界.文献［6］在单机环境下，既考虑了顾客的非同质时效函数，又考虑了供应方的目标，最终给出一种求解具有良好全局性能的Nash均衡调度的算法.

但是，在很多情况下顾客对时效的要求可能很复杂，除了能够反映对于等待敏感程度的时效函数之外，顾客通常还会提出一个最终的交货时间要求，即交期约束.而这一点是现有针对非同质顾客的运作研究还没有充分考虑的.

为此，本文在并行机下考虑顾客除具有不同的时效函数外，还具有各自的交期约束的情况.并行机拥有者要在实现自身利益最大化的同时，兼顾顾客的时效函数，并满足交期约束.首先，对于非同质顾客这一多人多目标问题，建立基于非合作博弈的数学模型，并采用Nash均衡调度概念描述模型的解.继而，针对并行机的物理约束和顾客的交期约束，利用拉格朗日松弛建立相应的松弛模型，并由此设计出包含松弛、可行化调整和交互协调三步的启发式算法.最后，通过算例仿真验证本文提出方法的有效性.

1 问题描述与分析

选择并行机中的同速并行机作为供应方的生产环境.同速并行机的特点是所有机器具有相同加工功能和相同且恒定的加工速度.考虑一个n个任务和m台同速并行机调度问题.供应方具有目标函数M.同时，每个任务Ji都具有独立的时效函数fi（wi）和交期DLi要求，并对应一个独立的顾客.借鉴文献［6］在单机下的模型，可得到并行机中如下数学模型.

其中：ri，pi和Ci分别为Ji的到达、加工和完工时间，均为整数；wi是Ji加工前的等待时间，为优化的决策变量，满足式（3）；H 是规划时域，H 应足够大以完成所有任务的加工.

模型中，式（1）和（2）分别是任务时效函数和供应方的经济性指标，式（4）隐含了不可抢占约束，即任一任务必须连续加工直至完工.式（4）和（5）构成了机器容量约束，即任一机器在同一时刻最多只能加工一个任务.图1所示为模型中各变量图示.

图1 同速并行机变量图示Fig.1 Illustration of variables in parallel machine

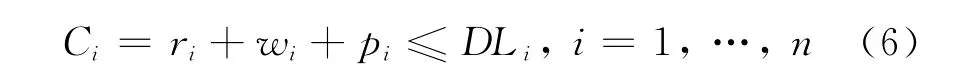
除了任务和供应方指标外，本文还考虑顾客对于任务完成最终期限的要求，描述为即任务Ji必须在DLi之前完成.交期DLi是由顾客i提出的.在供应能力有限时，可能无法满足所有任务交期要求.因此，约束（6）应是可协商的，本文用DLimax来表示Ji对其交期的最大容忍底线.

由式（1）～（6）构成了一个带约束的多人多目标优化问题.其中：式（1）和（2）是优化目标；式（3）～（5）是必须满足的物理约束；式（6）则是一种柔性约束.传统同速并行机调度研究仅考虑问题（2）～（5）.本文不仅考虑了任务时效（1），也同时考虑了约束（6）.对于如上的多人多目标问题，类似文献［5－6］，采用非合作博弈进行研究.为此，定义满足式（6）和式（7）的调度w＊（w＊＝（w＊1，…，w＊n））为模型的解，即Nash均衡调度.

Nash均衡调度w＊是顾客之间竞争现有生产资源的一种均衡结果，在这个解中，除破坏约束或恶化其他顾客的调度结果，否则每个顾客都不能改进自身的调度结果.但是，与博弈理论中个体理性与集体理性常常冲突的情况类似，Nash均衡调度w＊可能具有很差的全局性能［5］.为此，需要在多个Nash均衡调度w＊中选取具有良好全局性能指标（2）的结果.此外，过强的约束（6）可能导致没有满足任务交期要求的w＊，这将是后文要重点解决的一个问题.

2 算法设计

本节给出一种基于模型，并由供需各方参与决策的启发式算法求解上述问题.求解算法分为三阶段.

在第一阶段，首先将难约束松弛，其中不仅包括物理约束式（4）和（5），也包括交期要求式（6），得到只具有简单约束（3）的多人多目标优化问题.此时可以将文献［6］在单机下的算法扩展到同速并行机下，求出一个能较好满足各方经济性指标的Nash均衡调度.

第二阶段以第一阶段的解为基础，进行以可行化为目的的协调.即通过调整任务加工顺序，降低调度中的不可行程度，如果能得到可行的Nash均衡调度，则计算结束.否则，进入第三阶段.

第三阶段按设定规则与顾客协调，逐步修正部分交期约束，重复上面的步骤，直到出现供需各方接受的调度结果，即可行的Nash均衡结果.但是，如果所有顾客均放松其交货要求至DLmaxi，仍无法得到可行的解，则说明约束过紧，部分顾客无法成功竞争到机器资源.

2.1 松弛模型的建立和求解

为简化求解，考虑将难约束式（4）～（6）松弛，分别结合到各个任务的时效函数中，从而形成简单约束的多人多目标优化问题.其中，对式（4）～（6）采用不同的松弛方式.为将式（6）松弛，将各个Ji的时效函数fi中大于DLi的惩罚值设为一极大数R，如图2，得到新的时效函数fi′（wi）.这种刚性的惩罚方式，保证了计算结果必定满足约束式（6）.对式（4）和（5），将其通过拉格朗日乘子πk结合到各个任务的时效函数中.于是，可得松弛后的任务时效函数为

式中：πk可看作是供应方为其每段资源设定的价格，其值不小于0；Pik则是Ji为使用第k时段资源的支付.

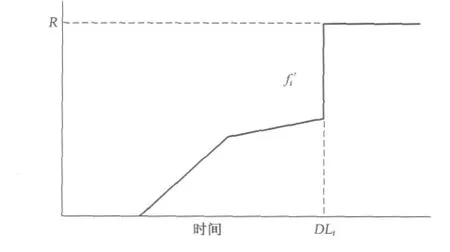
图2 式（6）松弛示意图Fig.2 Illustration of relaxing formula（6）

对于难约束松弛后的多人多目标模型，类似地，定义满足式（3）和（10）的调度 w′（w′＝（w′1，…，w′n））为松弛后模型的Nash均衡调度.

此处，可将文献［6］算法扩展到同速并行机下.基本思路为给定机器资源价格π，任务根据各自时效函数（8）并行地竞争机器资源，而机器则根据任务竞争结果和自身全局目标（2），改变资源价格π，以引导顾客自利行为结果趋向于全局优化.循环迭代，直至各方均不改变自身策略为止，最终产生一个具有良好全局目标（2）的w′.由此，设计如下的松弛模型求解算法.

（3）计算松弛后的全局性能指标Mr＝根据上一步中确定的任务开工顺序，采用List scheduling［7］方法可行化，并计算可行化调度的全局目标，作为

（5）r＝r＋1，转（1）.

注意到，与约束（6）的刚性松弛方式不同，容量约束的松弛采用柔性惩罚，故所得解w′满足式（6），但未必满足式（5）.下节需将w′可行化，以得到原模型的w＊.

2.2 可行化调整

为在可行化过程中区分各个任务交期的紧迫程度，首先定义顾客任务的自由度

Fi≤0表明Ji的完工时间没有违反约束（6），具有｜Fi｜的自由度；而当Fi＞0时，则说明其至少需要提前Fi个时间单位完工才能满足约束.实际生产环境中，供应方可根据任务的时效函数情况对任务设定相应的优先级.对于具有高优先级的任务，应尽量保证其完工时间在交期要求之前.

如前所述，w′未必满足式（5）.如果简单地使用List Scheduling［7］方法将 w′可行化，使其不违反式（5），得出的结果可能违反约束（6）.为此，设计一种深度搜索算法，其指导思想是根据先约束后指标，先物理约束后任务要求的顺序对w′进行改造.目的是在保证满足物理约束前提下，减少违反约束（6）的任务数目，经济性指标则被放到最次的位置.从而形成一个满足全部物理约束和部分交货要求的Nash均衡调度w＊，并由此判定问题可行性，给出供交互协调的定量信息.这种处理方式的本质是在保证可行的前提下最大限度保留了对优化的要求.

算法采用滚动的方式，不断地根据任务优先级和自由度局部地调整其加工顺序，包括确定局部子问题、调度子问题、执行子问题的部分解.其中，局部子问题的选择采用文献［8］中的冲突窗口方式，即选择w′中最靠前的任意两个之间相互重叠的任务（后任务的开工时间大于前任务的完工时间）集合作为当前子问题，其优点在于准确地考虑了当前可能加工的任务.子问题调度则主要根据任务自由度和优先级对第一阶段结果进行调整.每次迭代只确定一个任务.具体算法如下所述.

（1）定义S为w′中所有任务集合，迭代次数r＝0，r次迭代时机器最早空闲时间为Br，B0＝0.按任务在调度w′中的开工顺序给所有任务编号；开工时间相同的，则按其当前的优先级由大到小顺序编号；若开工时间与优先级均相同，则按其加工时间由小到大顺序编号.

（2）按时间轴由小到大的顺序，在S中寻找第一个局部子问题任务集合I（r）.显然有任意Jt，Jt＋1∈I（r）满足rt＋wt≤rt＋1＋wt＋1＜rt＋wt＋pt.按List scheduling将I（r）中任务可行化.

（3）记当前I（r）中编号最小的任务为Ji.对于I（r）的可行化调度，如果 ∀Jk∈I（r）满足Fk≤0，则Ji的开工时间为 max｛ri，Br｝，S＝S－｛Ji｝，更新Br，转（5）.

（4）在集合I（r）的所有不满足约束（6）的任务中，记优先级别最高的为Jj，如果优先级别最高的有多个，则Jj为其中编号最小的.若Jj的优先级小于Ji，且Jj先加工，余者按List scheduling加工使得I（r）中违反约束（6）的任务个数减少，则Jj的开工时间为max｛rj，Br｝.或者Jj的优先级大于Ji，则Jj的开工时间为 max｛rj，Br｝，更新Br，S＝S－｛Jj｝.

（5）r＝r＋1，对于 ∀Jk∈S，如果rk＋wk＜Br，则令wk＝Br－rk.如果S不为空，则转（2）.

（6）反馈每个任务的自由度Fi，计算结束.

步骤（2）是寻找子问题，步骤（3）和（4）求解子问题，算法体现了前文所述的思路，即首要满足物理约束，然后再考虑如何减少违反约束式（6）的任务，而经济性指标被放到了最后.改造后所得结果必定满足物理约束.由算法过程可知，它符合Nash均衡调度w＊定义中的式（7）.所以，如果该结果也满足任务要求，则该结果就是可行的w＊，整个计算结束.否则，则需通过与顾客的交互，在一定程度上放松部分DLi值，以增加调度可行的可能性.

2.3 交互协调

该阶段是在可行化调整的计算结果，特别是任务自由度的基础上，依据顾客能够承受超期，供应方与顾客的交互协调过程.用协调因子ki（∈（0，1］）和DLimax两个常数来描述Ji在交互中的协调可能程度，它们均由顾客自己给定.

对于第二阶段的调度结果，如果Ji的自由度Fi大于0，其DLi能够增加的值记为εi，

如果计算过程中得到可行的w＊，则整个计算终止.否则，当最近两次迭代中均出现所有任务的εi＝0，且仍有部分任务的Fi＞0时，说明已没有协商余地，计算终止.此时，由于供应方能力的限制，已无法满足所有顾客.

3 仿真实例

考虑两同速并行机调度问题，供应方目标为最小化完工时间之和.顾客具有如图3所示的常用时效函数，其中：Ⅰ和Ⅱ型分别对应完工时间和延迟时间，文献［9］定义Ⅲ型时效函数如式（13）所示.

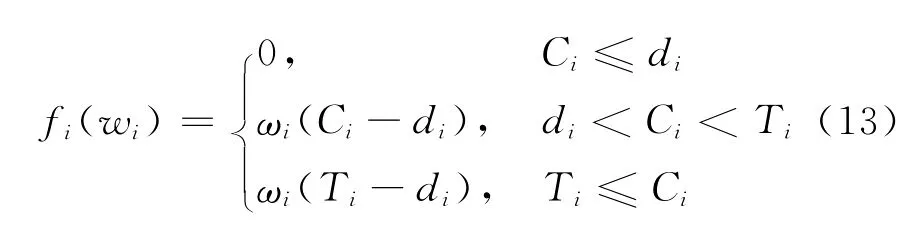
其中：Ti为大于di的常数.文献［6］改进Ⅲ型指标得Ⅳ型指标如式（14）所示.

Ⅳ型指标与Pinedo型［10］指标类似.图3（e）和3（f）给出了两种二次型指标Ⅴ型和Ⅵ型，分别是完工时间平方［11］和延期时间平方［12］.此外，还考虑Ⅶ型［13］和Ⅷ 型［14］两种指数型指标如式（15）和 （16）所示.

其中：0＜αi2＜1.

显然，上述8种指标均是随等待时间单调非减的.

本文仅考虑待加工任务信息公开，即完全信息的情况.具体信息如表1，其中：f1（w1）＝C1；f2（w2）＝max｛0，C2－d2｝，d2＝8；f3（w3）具有Ⅲ型指标，d3＝15，T3＝20，ω3＝1；f4（w4）为Ⅳ型，其中：d4＝15，T4＝22，ω41＝1，ω42＝0.5；f5（w5）＝C25；当C6小于d6（＝25）时，f6（w6）为0，否则为（C6－d6）2；f7（w7）和f8（w8）为Ⅶ和Ⅷ型指标，其中：α71＝5，α72＝0.5，α8＝1，d8＝25.

根据任务特点确定其优先级：具有线性指标的J1，J2，J3，J4优先级为1，J7虽为指数型指标，注意到它具有固定的上限，所以设定它的优先级也为1；具有2次型指标的J5和J6优先级为2；J8优先级最高，为3.

表1 待加工任务信息Table 1 Information of tasks

运用本文算法，对上述问题采用Visual Studio 2010编程，在主频为2.53GHz的电脑上进行运算.第一轮计算中，第一阶段的w′计算结果如表2所示，显然，该结果满足式（6），但不满足式（5）.经第二阶段计算，得到调度如表3所示，此调度结果很好地平衡了供需之间的成本，通过放弃部分全局目标，获得了较好的顾客加工成本，但是，该结果不能满足J3和J7的交货约束式（6）.为此，对J3和J7进行交互协调，如J3和J7的协调因子k3＝0.5，k7＝0.6，DLmax3＝35，DLmax7＝25，修正后的DL3和DL7分别为30和25.将J3和J7的优先级别分别加1，然后进入第二轮计算，两阶段计算结果如表4所示.此结果可行，计算结束.

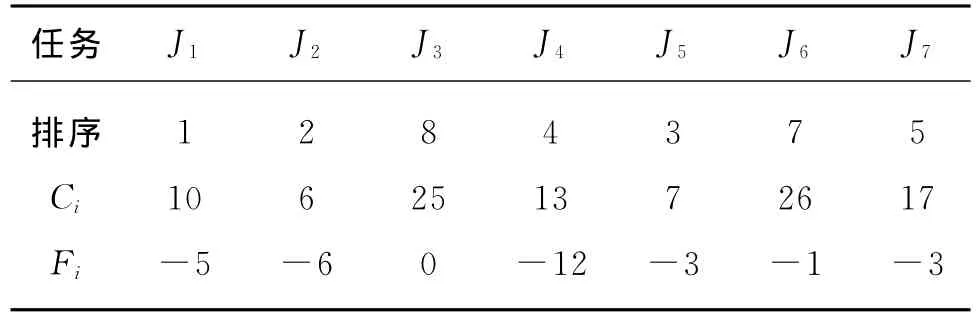
表2 第一轮第一阶段计算结果Table 2 Computing results of the 1st period in the 1st round

表3 第一轮第二阶段计算结果Table 3 Computing results of the 2nd period in the 1st round

表4 第二轮两阶段计算结果Table 4 Computing results of the 2nd period in the 2nd round

观察表3和4中的∑Ci和∑fi值，在不断调整以满足顾客交货要求的过程中，对于经济性指标的要求逐渐被弱化.这一现象是必然的，与前文所述一致.

4 结 语

顾客时效和交期要求客观存在且有差异，不应被同质化.本文在同速并行机下针对具有交期约束的非同质顾客，展开调度建模与算法研究.研究从竞争调度的角度，采用非合作博弈建立了问题的模型，并设计了一种三阶段的求解算法.首先模拟顾客对资源的竞争过程，给出一个考虑各方面优化指标和交货要求的初始调度.然后，进行可行化调整.由于可能存在约束过紧导致无可行解的情况，为此，最后通过一种简单有效的交互方式来予以协调解决.通过算例仿真验证所提方法的有效性.研究结果为这类问题的解决提供了辅助决策依据.本文假设顾客信息为已知，即完全信息，而不完全信息的情况则有待今后的进一步研究.

［1］陈剑，张楠.针对等待敏感顾客的缺货补偿与库存策略研究［J］.管理科学学报，2008，11（3）：53－62.

［2］MAISTER D H.The psychology of waiting lines［M］//CZEPIEL J A，SOLOMON M R，SURPRENANT C F.The service encounter：Managing employee/customer interaction in service businesses. Lexington： Lexington Books，1985：113－123.

［3］MURPHY P R J，WOOD D F.当代物流学［M］.北京：中国人民大学出版社，2009.

［4］KENNETH R B，SMITH J C.A multiple－criterion model for machine scheduling［J］.Journal of Scheduling，2003，6（1）：7－16.

［5］王长军，贾永基，徐琪，等.并行机下独立任务调度的无秩序代价分析［J］.管理科学学报，2010，13（5）：44－50，81.

［6］王长军，王志宏，贾永基.单机排序模型下自利任务的无秩序代价分析与机制设计［J］.东华大学学报：自然科学版，2010，36（6）：680－685，702.

［7］LUH P B，HOITOMT D J， MAX E，et al.Schedule generation and reconfiguration for parallel machines［J］.IEEE Transactions on Robotics and Automation，1990，6（6）：687－696.

［8］WANG C J，XI Y G.A rolling optimization algorithm based on collision window for single machine scheduling problem［J］.Journal of Systems Engineering and Electronics，2005，16（4）：816－822.

［9］KETHLEYA R B，BAHARAM A.Single machine scheduling to minimize total weighted late work：A comparison of scheduling rules and search algorithms［J］.Computers ＆Industrial Engineering，2002，43（3）：509－528.

［10］PINEDO M.Scheduling：Theory，algorithms and systems［M］.New Jersey：Prentice Hall，1995.

［11］CHENG T E，LIU Z H.Parallel machine scheduling to minimize the sum of quadratic completion times［J］.IIE Transactions，2004，36（1）：11－17.

［12］SUN X Q，NOBLE J S， KLEIN C M.Single－machine scheduling with sequence dependent setup to minimize total weighted squared tardiness［J］.IIE Transactions，1999，31（2）：113－124.

［13］ROTHKOPF M H.Scheduling independent tasks on parallel processors［J］.Management Science，1966，12：437－447.

［14］CHEN B，POTTS C N，WOEGINGER G J.A review of machine scheduling： Complexity， algorithms and approximation［M］//DU D Z，PARDALOS P M.Handbook of combinatorial optimization. Dordrecht： Kluwer Academic Publishers，1998：21－169.

Competitive Scheduling in Parallel Machine for Non－homogeneous Customers with Due－Date Constraints

WANG Chang－jun，JIA Yong－ji
（Glorious Sun School of Business and Management，Donghua University，Shanghai 200051，China）

A parallel machine scheduling problem with non－homogeneous customers is considered，in which different customers have heterogeneous waiting－sensitive characteristics and independent due－date constraints.Based on the practical problem，a noncooperative game is used to describe such issues and a heuristic algorithm including relaxation，feasibility and interactive coordination is designed.The effectiveness of the proposed method is further illustrated and validated via a computational experiment.

parallel machine scheduling；non－homogeneous customers；due－date；heuristic algorithm

C 935

A

2012－03－06

国家自然科学基金资助项目（70772073，60874076，71172174）；中央高校基本科研业务费专项资金资助项目（11D10826）

王长军（1976—），男，安徽巢湖人，讲师，博士，研究方向为调度理论与方法.E－mail：cjwang＠dhu.edu.cn

1671－0444（2012）03－0332－06