非标准安装下直齿轮啮合效率的计算及参数的确定*

王成范增

（济南大学机械工程学院，山东济南 250022）

提高机械产品的传动效率一直是人们关注的焦点［1］。齿轮传动作为应用最为广泛的一种传动方式，其传动效率的高低直接影响到环境污染和经济效益［2］。

确定齿轮传动效率的方法有查表、试验和计算3种。其中，试验法最为准确［3－5］，但缺点是检测的结果并不通用，且受很多因素的干扰。而查表法仅是给出一个范围，并不精确。因此，采用计算的方法更为可行［6］。笔者［7］曾提出了利用齿轮轮齿几何接触分析（TCA）和轮齿承载接触分析（LTCA）来计算齿轮的滑动摩擦功率损失。Xu H［2］提出了平行轴齿轮传动效率计算的模型。前述两种方法虽然能准确计算得到齿轮啮合功率损失，但所建模型均未直接建立功率损失与齿轮设计参数之间的关系。姚建初［6］通过计算任意啮合点处的瞬时啮合功率，利用连续函数积分中值定理，推导出了平均啮合效率的计算公式。笔者［8］在此基础上，推导出了直齿轮基本参数与啮合效率的关系。但上述两种方法在计算过程中均未考虑非标准安装情况。因此，所得出的结论存在局限性。

在齿轮实际安装过程中，存在非标准安装的情况。因此，本文在全面考虑直齿轮标准安装和非标准安装的基础上，推导出啮合效率的计算公式，进而得到设计参数对啮合效率的影响关系，为直齿轮设计参数的确定提供了理论指导。直齿轮啮合效率的计算及设计参数确定的流程见图1。

1 任意啮合点处的啮合效率

设图2和图3中渐开线齿廓1和2在任意点k接触，n－n为渐开线齿廓的啮合线，设轮1为主动轮。v1、v2分别为轮廓1和2在k点处的速度，α1、α2为v1、v2与啮合线的夹角（即齿廓压力角）。F12为轮1作用于轮2的合力，F21为轮2作用于轮1的反力，它们大小相等，方向相反，且与啮合线的夹角为φ（摩擦角）。

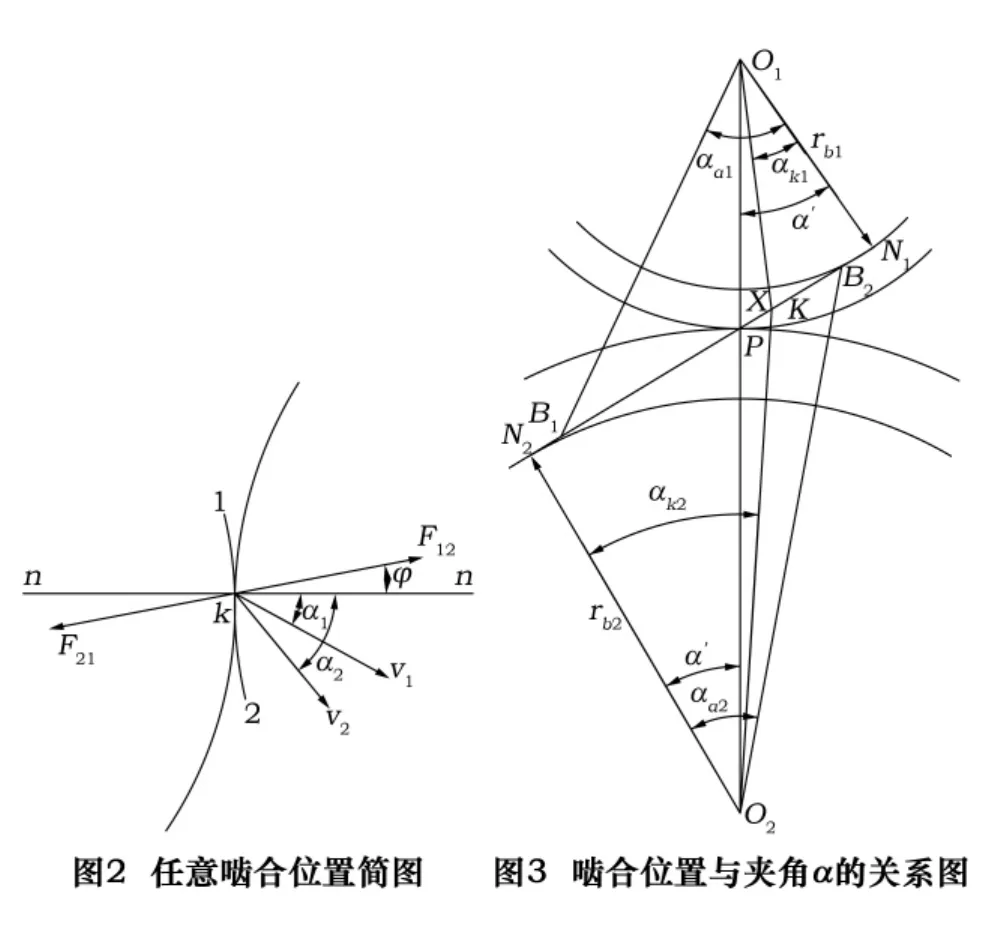
当接触点k位于节点P的右端（即PB2段）时，α1＜α2。此时，k点处的驱动功率为

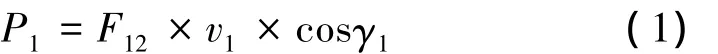
工作阻力功率为

式中:γi=αi+φ（i=1，2）。

根据平面啮合的基本定理［8］

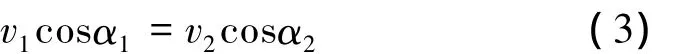
则k点处的啮合效率为

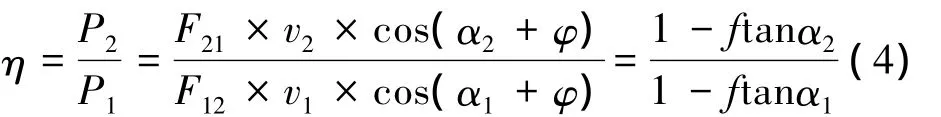
当啮合点k在节点P的左端（即PB1段）时，α1＞α2，通过计算得［8］

式中:f为摩擦因数。

2 设计参数与啮合效率关系式的推导

根据文献［8］，利用连续函数积分中值定理，用齿轮传动的平均啮合效率来代替齿轮传动的啮合效率。首先利用式（4）和（5），求出任意啮合点处的啮合效率（即瞬时啮合效率）。然后通过分段积分求出实际啮合线上总的啮合效率。最后，用总的啮合效率除以实际啮合线长度得到平均啮合效率。

在图3中，齿轮实际啮合线为B1B2，P为啮合节点，通过上面的计算可知，PB1段和PB2段瞬时啮合效率的计算公式不同，因此，分别对PB1段和PB2段进行积分。由图3及文献［9］可知:

式中:rb1、rb2分别为齿轮1、2的基圆半径;α'为啮合角。

将坐标原点取在节点P处，方向如图3所示。

2.1 计算PB1段的啮合效率

该啮合段速度与啮合线夹角α1＞α2，因此，啮合效率的计算公式为式（5）。由图3，PB1段速度同啮合线夹角α与啮合点位置x的关系可表示为

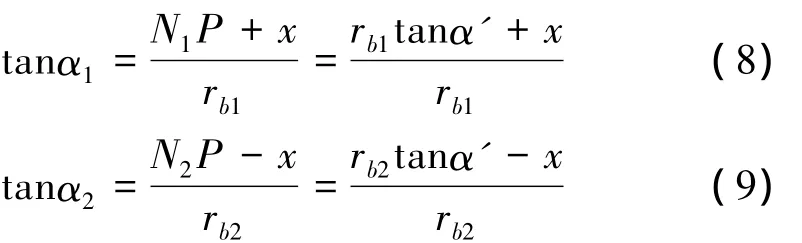
将式（8）和（9）代入式（5），得

在PB1段上对η1（x）进行积分，即

根据文献［9］:

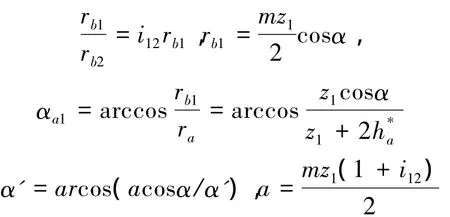
式中:m为齿轮模数;z1为齿轮齿数;i12为传动比为齿顶高系数。

将以上关系式代入式（11）并整理得:

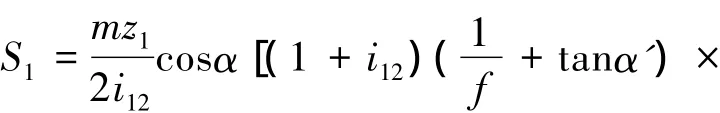
2.2 计算PB2段的啮合效率

该啮合段速度与啮合线夹角α1＜α2，因此，啮合效率的计算公式为式（4）。由图3，PB2段速度同啮合线夹角α与啮合点坐标x的关系可表示为在PB1段上的啮合效率为:

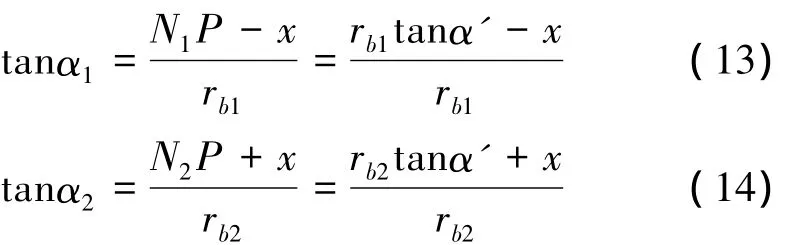
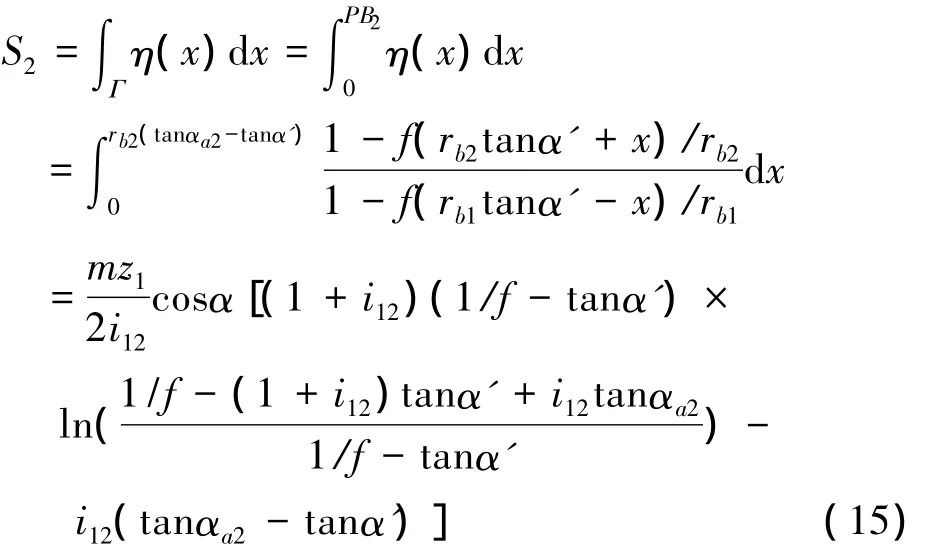
2.3 计算直齿轮的啮合效率

根据文献［9］，B1B2段的长度为

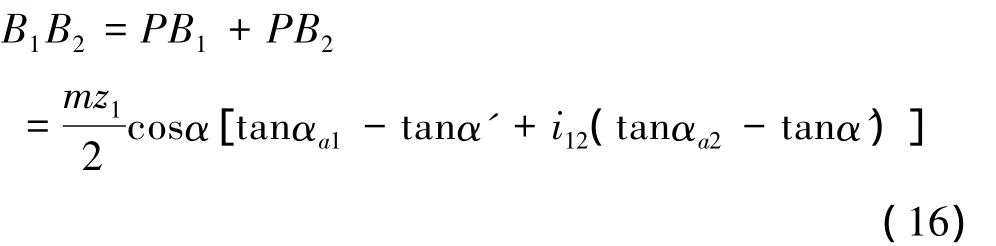
这里，我们用平均啮合效率来代替齿轮传动的啮合效率，因此直齿轮传动的啮合效率为

3 直齿轮设计参数与啮合效率之间的关系

上面我们推导出了齿轮设计参数与啮合效率之间的关系式，从中可以看出，式中不包含顶隙系数c*和齿宽B。同时，式中我们用i12z1代替z2。下面分别讨论齿数z1、模数m、传动比i12、压力角 α、齿顶高系数和中心距安装误差Δa对啮合效率η的影响。取f=0.05，z1=20，i12=2，α=20°，=1，m=2 mm 和 Δa=1 mm。针对相关参数再具体设定其变化区间，基于Matlab编程绘出相应的关系曲线图。

3.1 齿数z1对啮合效率η的影响

取z1=20～100，其他参数不变。根据上述公式，利用Matlab编程绘出的齿数z1与啮合效率η关系如图4所示。从图4中可以看出，η随着z1的增加而增大。但当z1超过一定数值后，效率增加趋向平缓。同时，根据齿轮传动设计参数选择理论，增加齿数，有利于提高重合度，改善传动的平稳性，但在齿轮尺寸一定的情况下，增加齿数将引起模数的减小，从而降低齿轮的弯曲强度。

3.2 模数m对啮合效率η的影响

取m=2～8 mm，其他参数不变。根据上述公式，利用Matlab编程绘出的模数m与啮合效率η关系如图5所示。在图5中，η随着m的增大而减小。当m超过一定数值后，效率的减小趋向平缓。同时，根据齿轮传动设计参数选择理论，在强度和结构允许的条件下，应选取较小的模数。

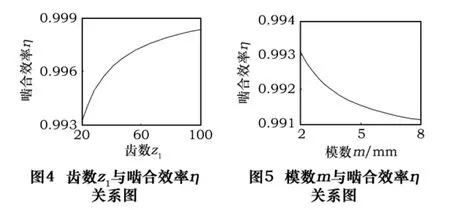
3.3 传动比i12对啮合效率η的影响

取i12=1～10，其他参数不变。根据上述公式，利用Matlab编程绘出的传动比i12与啮合效率η关系如图6所示。在图6中，随着i12的增大，η也随之增加。当i12超过一定数值后，效率增加趋向平缓。

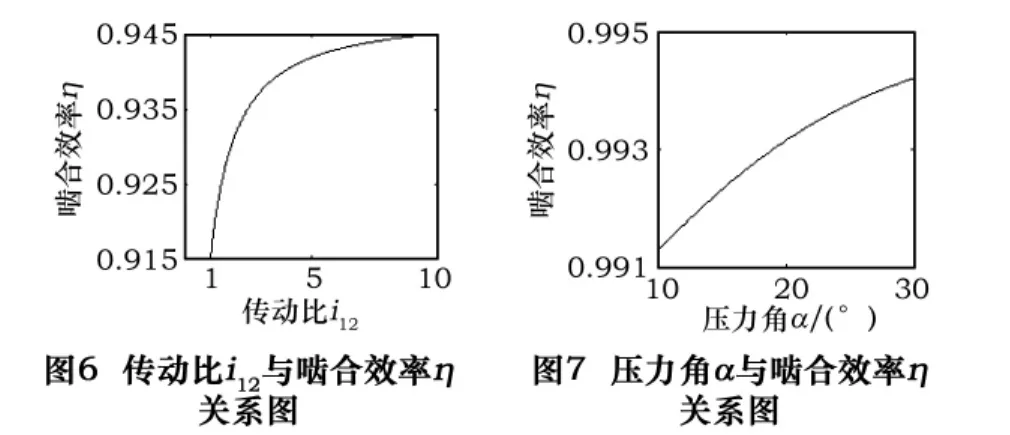
3.4 压力角α对啮合效率η的影响

取α=10°～30°，其他参数不变。根据上述公式，利用Matlab编程绘出的压力角α与啮合效率η关系如图7所示。从图7中可看出，η随着α的增大而增大。当α超过一定数值后，效率增大趋向平缓。同时，根据齿轮传动设计参数选择理论，增大压力角，有利于提高齿轮传动的弯曲强度及接触强度，减小不发生根切的最少齿数。但这也导致重合度降低，传动平稳性差，噪声增大，径向力增大。

3.5 齿顶高系数ha*对啮合效率η的影响

取=0.8～1.2，其他参数不变。根据上述公式，利用Matlab编程绘出的齿顶高系数与啮合效率η关系如图8所示。在图8中，随着的增大，η随之减小。同时，根据齿轮传动设计参数选择理论，减小，可减少不发生根切的最少齿数，但减小将使重合度降低，传动平稳性差，噪声增大。

3.6 安装误差Δa对啮合效率的影响

取中心距安装误差Δa=0～2 mm，其他参数不变。根据上述公式，利用Matlab编程绘出的安装误差Δa与啮合效率η关系如图9所示。在图9中，随着Δa的增大，η随之增大。同时，根据齿轮传动设计参数选择理论，中心距安装误差过大，齿轮将不能正常啮合。

4 算例

设计某螺旋输送机传动装置中的直齿轮。其工作机的功率为2.1 kW，转速为105 r/min。通过传动比分配，i12=4.5。分别按齿根弯曲和齿面接触强度计算得到模数，经比较取m≥2.41 mm。根据GB1357－87，标准模数可以取为m=2.5 mm或m=3 mm。在齿轮尺寸一定的情况下，模数与齿数成反比，即①m=2.5 mm时，z1=22;②m=3 mm时，z1=18。从上文结论中可以得到，选取小的模数/较多的齿数，有利于提高啮合效率。分别计算两种方案对应的效率（表1，取f=0.05）。从表1中可以看出，方案①的啮合效率要高于方案②，即与所得结论相符。

表1 满足强度情况下不同方案对应的啮合效率

5 结语

针对直齿轮标准安装和非标准安装的情况，推导出了齿轮设计参数与啮合效率之间的关系式，通过MATLAB编程绘制出了相应的关系曲线图，结合齿轮传动设计参数的选择理论得出以下结论:

（1）当承载能力主要取决于齿面接触强度时，选取较多的齿数有利于啮合效率的提高。

（2）在强度和结构允许的条件下，适当减小模数，有利于啮合效率的提高。

（3）传动比增大，啮合效率随之增大，但当达到一定程度后，趋向平缓。因此，对于多级齿轮传动，在总的传动比一定的情况下，合理分配传动比有利于提高整个齿轮传动系统的效率。

（4）压力角与啮合效率同方向变化，在保证传动平稳的前提下，适当增加压力角有利于啮合效率的提高。

（5）适当减小齿顶高系数有利于提高啮合效率。

（6）合理增加中心距，有利于啮合效率的提高。

因此，在满足强度、寿命和正确传动的前提下，应适当增加齿数、传动比、压力角和中心距，适当减小模数和齿顶高系数。同时采用合理的润滑，减小摩擦因数。

［1］Reuleaux，F.Friction in Tooth Gearing［J］.Trans.ASME，VIII，1886:45－85.

［2］Xu H，Kahraman A.Prediction of mechanical efficiency of parallel－axis gear pairs［J］.Journal of Mechanical Design，2007，129（1）:58－68.

［3］Aarthy Vaidyanathan，Tech B.An experimental investigation of helical gear efficiency［D］.A Thesis presented in Partial Fulfillment of the Requirements for The Degree of Master of Science in the Graduate School of the Ohio State University，2009.

［4］Petry－Johnson T T，A Kahraman，Anderson N E，et al.An Experimental Investigation of Spur Gear Efficiency［J］.Journal of Mechanical Design.2008，130（6）:062601.

［5］戴雪晴，周哲波.齿轮几何参数对传动效率影响的实验［J］.上海交通大学学报，2006，40（7）:1226－1229.

［6］姚建初，陈义保，周济，等.齿轮传动啮合效率计算方法的研究［J］.机械工程学报，2001，37（11）:18－21.

［7］王成，方宗德，贾海涛.斜齿轮滑动摩擦功率损失的计算［J］.燕山大学学报，2009，33（2）:99－102.

［8］王成，方宗德，张顺利.基于啮合效率下齿轮基本参数的选择［J］.机床与液压，2007，35（9）:10－12.

［9］郑文纬，吴克坚.机械原理［M］.7 版.北京:高等教育出版社，2010.